Глубоковский Н., проф. Православная пасхалия и общедоступные руководства по хронологии

Журнал «Христианское чтение», СПБ., 1892 г. №5-6.

Файл в формате PDF взят с сайта www.spbda.ru

Разбивка страниц настоящей электронной статьи соответствует оригиналу.

Н. Н. Глубоковский

ПРАВОСЛАВНАЯ ПАСХАЛИЯ И ОБЩЕДОСТУПНЫЕ РУКОВОДСТВА ПО ХРОНОЛОГИИ

В статье «О реформе православного календаря», помещенной в «Церковном Вестнике» (№ 6 за 1892 г., стран. 86—89), были указаны истинные основы христианского летосчисления и приведены мотивы, по которым мы считаем пока более соответствующим ему стиль русский,—старый или юлианский, так как только при нем одном удовлетворяется каноническое требование апостольских правил и Никейского собора, что пасха христианская не должна ни предупреждать еврейскую, ни совпадать с нею во дне, между тем на Западе бывает и то и другое. Не все остались довольны нашими замечаниями, а некоторые поняли их в том смысле, что мы ратуем против научной точности, когда речь шла лишь о тон, что последняя не должна изгонять и уничтожать канонов, которым в вопросе о календаре христианском принадлежит, по крайней мере, равное значение. Впрочем, важно уже и то, что даже самый горячий защитник «календарной реформации», г. Филиппов, признал законность указанной нами постановки дела и обещал приспособить к ней свою систему (см. газету День, 1892 г., №№ 1327 и 1347). Однако, если и появится проект, безукоризненный и в церковной и в научном отношениях, — перемена принятого теперь календаря не может случиться скоро; при том же, во всяком случае пасхалия, в существенном, должна сохраниться в прежнем виде. Поэтому в практических интересах не бесполезно

399

400

указать некоторые простейшие способы относительно нахождения важнейших хронологических пунктов по нашему старому стилю.

Для ближайших своих целей мы сначала постараемся объяснить прилагаемую к церковным месяцесловам таблицу под заглавием «Ключ вкратце», где все вычисления построены на воскресных буквах или вруцелетиях.

Первый вопрос в хронологии—найти правило для определения дня недели в данное число месяца, принимая, что создание мира было в пятницу первого марта за 5508 лет до Рожд. Хр., как это усвоено пасхальным летосчислением. Для сего все дни недели обозначаются славянскими буквами в следующем порядке: Г— пятница, В—суббота, А—воскресенье, З—понедельник, S— вторник, Å—среда, Д—четверг. В первый год все дни его будут соответствовать этим буквам и воскресенье всегда совпадает с А; но так как количество недель в году не полное (52 нед. + 1 день или, в високосе, 52 нед. + 2 дня), то и буквы воскресные в разные годы будут неодинаковыми, станут приходиться не на одни и те же дни. Воскресные буквы, очевидно, должны переменяться, что продолжается в течении 28 лет (каковой период называется кругом солнца), после чего они опять приникают прежний порядок за все следующие 28 годов. Отсюда понятно, что если нам известно вруцелетие для данного года, то мы знаем уже, на какой день недели падало его начало или 1-ое марта. Посему для определения воскресной буквы данного года нужно отыскать его положение в 28-летнем периоде. Для этого избранный год слагают с 5508 г. от сотворения мира и делят на 28; частное (0= 28) покажет, которым он будет в круге солнца. Для упрощения работы можно просто прилагать только 20 (ибо за 20 лет до Р. Хр. начался новый 197-йкруг солнца). По остатку в таблице находим ключевую букву, напр. для 12—А, для 14—Г, для 26—Д. После этого уже не трудно приурочить и каждый день этого года к соответствующей букве. Для этого нужно сосчитать количество дней от 1 марта по взятое число, отнять три (ибо 1 марта равняется пятнице) и разделить на семь; частное будет равняться по порядку одной из

401

следующих букв: З, S, Å, Д, Г, В, А, причем 0=7 или А. Теперь можно найти день недели для любого числа какого угодно года. Возьмем хотя бы 15-е число месяца мая 1892 г. 20 + 1892=1912:28 дает остаток 8, т. е. его вруцелетие Г. До 15 мая протекло с 1 марта (31 + 304 + 15) дней 76—3=73 : 7 дает остаток 3; следовательно для 15 мая буквою будет сей год служит Å. Считая Г за воскресенье, по первому порядку букв увидим, что Å упадет на пятницу, когда и придется в 1892 г. день 15-го мая. Само собою понятно, что для нынешнего гражданского стиля ключевую букву для января и февраля нужно брать из предыдущего года, ибо в пасхальном летосчислении, с 1-го марта, эти месяца составляют конец старого года, а не начало нового. Этого же результата можно достигнуть еще проще по формуле проф. Д. Перевощикова. Предыдущий данному год разделить на 4 и найти число дней от 1 января до избранного числа; сложить все эти числа и сумму разделить на 7:—остаток покажет день, если считать воскресенье=1 и т. д., суббота=7 или 0. Так, для 15 мая 1892 г. имеем: 1891 + (1891:4=)472+(31+29+31+30+14 =) 135 = 2498:7 дает остаток 6, равняющийся пятнице.

Но для православного летосчисления еще важнее знать, в какое число придется в данном году пасха, так как именно этот праздник лежит в его основе. Он совершается: а) после первого весеннего полнолуния, если оно приходится в день или в след за весенним равноденствием, б) после второго (т. е. апрельского), когда мартовское будет раньше указанных сроков, в) в первый воскресный день или в следующий, если пасхальное полнолуние упадет на пятницу, субботу и воскресенье. Значит, в этот случае нужно отыскать число пасхального полнолуния ? соответствующий ему день недели. Так как 12 лунных месяцев—от полнолуния до полнолуния— меньше юлианского года почта на 11 дней, то фазы луны для каждого года будут неодинакова; иначе сказать: не в каждом году полнолуние будет совпадать с его началом. Замечено, что фазы луны повторяются чрез 19 лет (Метонов цикл): это

402

круг луны, по отношению к которому необходимо определить, какое место занимает в нем взятый год. Для сего нужно вычислить, сколько прошло полных лунных кругов; остаток, называемый золотым числом, покажет искомую величину. В церковном времясчислении началом кругов луны берется 5508 от С. М., при чем с (5508 : 19=289+) 17 года до Р. Хр. начинается новый (290-й) круг. Но оказалось, что новолуние христианской эры совпадало с 1 января за год до Р. Хр. и, следовательно, церковное летосчисление, полагающее этот пункт в (5508+2=) 5510 г. вместо 5507 г., отстает в кругах луны на 3 года; потому, прибавив к избранному году 17 и разделив сумму на 19, мы подучим только круг луны, а для отыскания истинного золотого числа должны присовокупить еще 3 и из суммы, если она больше 19, вычесть цифру 19. Помножив золотое число на 11 и разделив на 30, найдем в частном — количество полных кругов за этот период и в остатке (в астрономии «эпакта», в церковном времясчислении основание)—ее действительное положение в марте взятого года (ибо январь и февраль составляют две полная лунации). Новолуние бывает черев 30 дней: следовательно оно=30 — основание; полнолуние же происходит чрез 15 дней и следовательно= 30 — основание+15. Оно и признается пасхальным, если будет больше 19 или если будет равняться 19(-му числу марта); в противном случае, оно не будет таковым,—и истинное пасхальное полнолуние наступит в апреле, для чего слагаем мартовское с 30 и вычитаем 31 день марта.

Так для 1892 г.: круг луны = (1892+17 = 1909:19= 100+) 9, золотое число=9+3=12; основание=(12 х 11 : 30=4+) 12; новолуние=(30—12=) 18, полнолуние (18+15)=33 марта или (33—31) 2 апреля. День недели находится, как указано выше. Вруцелетие для 1892 г. Г; с 1 марта до 2 апреля прошло 33 дня; поэтому ему будет соответствовать (33—3 : 7= 4+) 2 или буква S, которая упадет на четверг. Пасха будет в ближайшее воскресенье или чрез 3 дня, т. е. 5 апреля 1).

1) Об отношении принятых «пасхальных» элементов к астроно-

403

Определив все основания за 19-летний период, мы найден, что пасха может быть только в границах между 22 марта и 25 апреля, т. е. в один из 85 дней между ними. Каждый из них обозначается буквами славянского алфавита во порядку (А=1, S=8, З=9, Ѽ=24, Ѫ=34, Ѧ=35), называемые «ключевыми» или «ключами границ»; они указывают, на сколько дней данная пасха удалена от 21 марта. Так, сей год она отстоит та (31+5=36—21=) 15 дней, и ключевою буквой для него будет Н (наш).

По этан ключевым буквам отыскиваются все праздники и посты следующих образом:

1) Преполовение равняется ключевой букве +14 апреля, т. е. Н или 15+14 апр.=29 апреля;

2) Вознесение Н+ 29 апр.=44—30=14 мая;

3) Троицын день Н+9 мая=24 мая;

4) мясопуст или заговенье пред Петровым постом Н+16 мая=31 мая (след., пост с 1-го июня);

5) Великий пост: в простом году ключ+24 января и в високосе ключ+25 января (для 1892 г.: 15+25 января)= мясопуст (40—31—9 февраля), а чрез 7 дней будет сыропуст или полное заговенье (для 1892 г.: 9 февр.+7=16 февраля);

6) Продолжение мясоястия в простом году=ключевой букве + 31 и в високосном= ключевой букве 32; для 1892 г. имеем 15+32=47 или 6 недель и пять дней.

К сказанному следует прибавить пояснение двух терминов. Индиктом называется пятнадцатилетний период, почему, сложив данный год с 5508 от С. М. и разделив на 15, получим число прошедших индиктов и в остатке—год нового индикта. Для 1892 г.: 1892 + 5508 = 7400 : 15 = 493 и остаток

мическим и о необходимости удерживать первые даже при несоответствии ах последним см. в статье проф. Моск. духовной академия Д. Ф. Голубинского «О времени празднования пасхи у христиан востока и запада» в апрельском (4-м) №-ре «Богословского Вестника» за 1892 г., стр. 73—88.

404

5, т. е. этот год 5-й в 494 индикте. Для краткости индиктами называют самые остатки (для 1892 г. будет индикт 5-й или Д). Его отличают от «индиктиона» или «великого пасхального круга», обнимающего 532 г. (19-летний круг луны, помноженный на 28-летний круг солнца), после которого числа Пасхи и подвижные праздники возвращаются к прежнему порядку. Если такой индиктион есть, стоит только найти положение данного года в нем, — и тогда соответствующая таблица укажет все нужные праздники. 1892 год будет 484-м в 14-м индиктионе (1892 + 5508 = 7400 : 532 = 13 и 484 в остатке).

По 7000 г. от С. М. (или по 1492 от Р. X.) включительно год на Руси считался с 1 марта, а с 7001 по 7207 С. М. (1669 P. X.)—с 1 сентября; с 7208 (или 1700 от Р. Хр.) с 1 января. При вычислениях древних дать и переводе их на наше гражданское (январское) летосчисление в годах мартовских или пасхальных для месяцев января и февраля нужно вычитать из них 5507 л., в годах сентябрьских или церковных для месяцев сентября, ноября и декабря нужно вычитать 5509 л.; когда год сентябрьский переводится на мартовский, вычитаем из него 5509 лет для месяцев с сентября по февраль; наоборот—вычитаем для тех же месяцев 5507 лет.

Мы объяснили все элементы церковного календаря и указали способы, как нужно пользоваться ими для различных вычислений. На основании их же можно делать и проверку исторических данных. Так, в «Псковской летописи» значится: «Индикта 1, в лето 6497, ключ границ 100, круг солнца 28, вруце лето 7, а луне круг 17, а жидом пасха 5 апреля в пятницу, а христианом пасха апреля 8». 6497 от деления на 15 дает 433 с остатком 2, т. е. второй индикт. Ясно, что здесь счет ведется по сентябрьскому году; потому из него вычитается уже 5509 лет. Получается 988. Сложенный с 5508 и разделенный на 28, он дает 28-й круг солнца. 988+17 : 19 дает 17-й круг луны. В 28 круге солнца вруцелетие З или 7. Золотое число (17 + 3 = 20—19)— 1; основание 1 X 11 = 11,

405

потому новолуние 30 — 11 = 19 марта. Полнолуние 19+15 = 34—31 — 3 апреля. 31 + 3—3 : 7 дает остаток 3 или буква Å, которая при вруцелетии S будет соответствовать вторнику. Отсюда 5 апр. будет равняться четвергу, но не пятнице (значит, в летописи ошибка или в дне или числе), а пасха православная в ближайшее воскресенье упадет на 8 апр. От 1 марта по это число прошло 39 дней, след. от 21 марта оно отстоит на 39—21 или 18, каковая буква в ключах приходится на Р, а она значит 100.

Из представленного нами разбора видно однако же, что, не смотря на несложность, вычисление указанными приемами требует большой ловкости, сноровки и «чистоты», да еще некоторых таблиц. Поэтому издавна придумывались разные способы для облегчения отыскивания, по крайней мере, дня пасхи. Так в старинной книге «Рука Богогословля» и рукописи Имп. Публ. Библиотеки № 199 имеется «Ручная Пасхалия», где все пасхальные термины приурочены к суставам пальцев. Это наглядно, но дела не облегчает, ибо требует большой памяти. Единственно верным методом остается здесь чисто математический. У нас пользуется известностью формула проф. А. Н. Савича, признанная акад. Буняковским весьма остроумною, но в ней важную роль играют «условия» или «оговорки", затрудняющие процесс. Без сомнения, она точна, но все же несколько сложна и при недостаточной внимательности может вести к неверным выводам. И мы лично знаем, как один преподаватель математики высчитал по ней пасху в среду. Со стороны просты лучшею остается формула Гауса, по которой можно находить и пасху православную и западную,—по грегорианскому календарю. Тут на первом месте стоят элементы М и Ν. Для старого стиля они постоянны: М = 15, N = 6; но в новом они меняются: по таблице Деламбера для годов с 1800 по 1899—М= 23, N=4, с 1900 по 1999—М= 24, N=5, с 2000 по 2099—М= 24, N= 5. Затем система Гауса заключается в следующем:

1) Взятый год нужно разделить на 19, на 4 и на 7; получим остатки а, b и с. 2) Сумму 19.  а + Ж разделить на

406 

30;—остаток будет d. 3) Сумму 2. b + 4. с + 6.d + N разделить на 7; — остаток будет е. 4) Пасха будет в этом году или 22 + d + е марта, или (d + е — 9) апреля. Отсюда можно определить пасху православную и западную для 1892 г. В первом случае мы имеем: а (1892 : 19) = 11; b (1892 : 4) = О; с (1892 : 7) = 2; d (19 X 11 + 15: 30) = 14; е (2 Х 0 + 4 Х 2 + 6 X 14 + 6 : 7) = О. Пасха будет 22 + 14 + 0 = 36 марта или (36—31) 5 апреля. Для нового стиля d= (19. а + 23 или 19 X 11 + 23 =) 232 : 30 = 22; е — (2.b  + 4. с + 6. d + 4 или 0 = 8 + 132 + 4 =) 144. 7 = 4; поэтому сей год пасха на Западе будет 22 + 22 + 4 = 48 марта или 17 апреля, т. е. в один день с православною, поелику у «грегорианцев» числа считают на 12 дней вперед против нашего.

Однако же и формула Гауса—при всех своих достоинствах— не может считаться самою простою. Помимо привходящих элементов М и N, она требует полнить порядок действий и в самых вычислениях дает слишком большие числа, при которых скорее возможны ошибки и недосмотры. Поэтому не безынтересно сообщить о новой попытке по этому предмету г. Сплендорова, опубликованной в №-ре 6 (за 15-ое марта) «Известий по Казанской епархии» за 1892 г. (стран. 133—138); она чужда этих недостатков и наглядна, а анализ ее открывает возможность вычисления дня празднования пасхи без всяких формул при помощи четырех простых арифметических действий.

Вот сущность соображений автора. Пасха совершается в одно из чисел с 22-го марта по 25-ое апреля включительно, т. е. в течение 35 дней, или семи недель. Из них образуется таблица (№ 3-й) в пять вертикальных и семь горизонтальных колонн. Соответственно этому ряду составляется второй—точно также в пять вертикальных и семь горизонтальных рядов — из чисел с 0 по 27 включительно, но с таким расчетом, чтобы чрез каждые четыре цифры оставалось одно пустое место (№ 2).  Сверх сего необходима еще третья таблица, которая—подобно двум первым—состоит из пяти вертикальных

407

и семи горизонтальных рядов. Она получается следующею способом. На последнем (седьмом) месте снизу в пятой вертикальной колонне слева пишется 1; каждая дальнейшая цифра должна быть больше предшествующей на 11 (т. е. вторая будет равняться 12, третья—23), во если она превысит 29, то из нее нужно вычесть 30 и продолжать таким же путем, пока не заполнятся все тридцать пять мест. После этого мы будем иметь следующую схему:

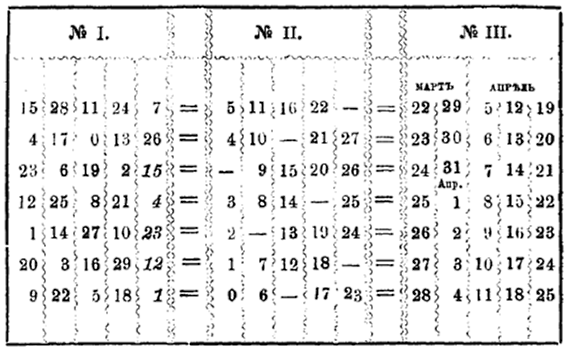
Теперь набранный год нужно разделить на 19 и 28 и приискать место остатков от деления в таблицах I и II; при этом пять последних (подчеркнутых) чисел пятой вертикальной колонны таблицы I не следует принимать во внимание, ибо они встречались ранее, так что дня остатков 15. 4. 23. 12 и 1 положение годов будет в первой, а не в пятой колонне. Если места остатков от деления года на 19 и 28 в таблицах I и II придутся на одной горизонтальной черте, то числом пасхи будет в III таблице то, которое находится на той же горизонтальной черте в вертикальной колонне, соответствующей колонне первого остатка в таблице I. Если остатки упадут не на одну и ту же горизонтальную линию, то в первой таблице нужно взять из следующих за остатком то число, которое бу-

408

лет по отношению ко второму именно в таком положении, и затем—соответственно ему—найти в III таблице требуемую дату. Так, от деления 1892 г. получаются остатки 11 и 16 на одной горизонтальной линия, причем 11 находятся в третьей колонне табл. I; поэтому пасха будет 5 апреля. 1893 г. дает остатки 12 и 17 не на одной горизонтальной черте; после 12 ближайшим числом в табл. I на той же линии будет 9, а ему в табл. III равняется 28 нарта. 1897 г. дает остатки 16 и 21 не на одной черте, причем после 16 в таблице I положению 21 таблицы II будет соответствовать 13, каковое в III таблице указывает на 13-ое апреля. Для 1907 г, остатки будут 7 и 3 не на одной горизонтальной линии, а после 7 в пятой колонне таблицы I положению второго остатка будет соответствовать цифра 4, для которой в таблице IIU имеем 22. Следовательно в 1907 г. пасха будет 22-го апреля.

Из сказанного видно, что в изложенной системе главную роль играет положение остатков от деления года на 19 и 28 в горизонтальных и вертикальных рядах в их взаимном отношении и соответственно числам с 22-го марта и 25-е апреля. Нет ли тут какого-нибудь общего закона?

Рассматривая предложенные таблицы с этой стороны, мы замечаем, что если данный остаток от деления года на 19 увеличить столькими десятками, сколько будет в остатке единиц от деления его на 3, и сумму вычесть из 46, то получив вертикальное и горизонтальное его положения в табл. I. Так 1894 г., деленный на 19, дает остаток 13; после деления его на 3 получаем в остатке 1 и потому увеличиваем на один десяток. 13 + 10 или 23, отнятые от 46, дают 23. Так как в каждой колонне семь мест, то для 1894 г. оно будет вторым в четвертой колонне, ибо 23 : 7 дают В полные ряда и в остатке 2, т. е. второе место ряда четвертого.

Во II таблице после каждого четвертого числа имеется пустое место; поэтому ко второму остатку нужно прибавить столько единиц, сколько раз содержится в нем 4, и сумму разделить на

409

сем: частное покажет, что он находится в следующем вертикальном ряде, а остаток—место его в последнем. 1894 г., разделенный на 28, дает в остатке 18, в котором четыре четверки (18 : 4 = 4 + 2). Поэтому 18 + 4 = 22 : 7 = 3+1; то есть для этого года во второй таблице будет место 1 (или второе, поскольку внизу первой колонны нуль) в четвертом ряде.

После этого требуется определить, совпадают ли эти места по горизонтальному направлению, — а если нет, то какой вертикальный ряд табл. I будет соответствовать взятому году. Первое, очевидно, случится только тогда, когда сумма их мест будет равна 7 (напр. для 1892 г. с остатками 11 и 16 имеем: 11 : 3 = 3 + 2.11.+20 =31; 46—31 = 15 : 7 = 2 +1; 16:4=4, поэтому 16+4=20: 7 = 2 + 6; 1 + 6 = 7); коль скоро этого нет, значит в горизонтальных рядах остатки этого года будут отстоять между собою на столько, на сколько сумма их мест в рядах вертикальных не хватает до 7, на каковую разность и нужно подвинуть вперед № места остатка первого. Для 1894 г. мы имеем 2 и 1; следовательно 2 + 1=3; 7—3=4; 23+4=27. Ясно, что для этого года пасха подвинулась вперед от 22 марта на 27 дней, из коих 10 дней (с 22 по 31-ое число марта) падает на март; поэтому, вычтя из 27 цифру 10, для пасхи сего года будем иметь 17-ое апреля.

По всем этим соображениям можно вычислить пасху и без всяких таблиц при помощи одних четырех арифметических действий. Вся операция будет заключаться в следующем (способ первый):

А) Взятый год нужно разделить на 19 и 28 и заметить полученные от деления остатки.

Б) Первый отток увеличить (прибавить к нему) столькими десятками, сколько подучится в остатке единиц от деления его на 3. Для 1895 г. остаток равняется 14; 14:3 = 4+2; следовательно получим 14+20 = 34.

Если остаток от деления года на 19 равняется нулю или 1 и 2, которые не делятся на три целым числом с остатком, то нужно прибавить столько десятков, сколько единиц такой оста-

410

ток показывает. Так, для годов с 1900 по 1902 получаются остатки: 0. 1 и 2; значит для них имеем 0. 11 и 22.

Если остаток делится на три вполне, то к нему не нужно делать никаких прибавлений. Посему, напр., 1898 : 19 = 99 + 12:3 = 4+0; потому берем просто 12. Для 1903 года принимают 3, ибо 3:3=1+0.

В) Найденное число вычитаем теперь из 46 и замечаем этот новый остаток; для 1895 г. получаем (46—34=) 12.

Если от вычитания получится число большее 30, то из него отнимаем еще 30. Для 1903 г. имеем (1903 : 19 = 100 + 3; 46 — 3 = 43 — 30 = ) 13.

Г) Последнее число В делим на семь и запоминаем остаток. Для 1903 года таковой будет равняться (13 : 7 = 1 +) 6.

Если при таком делении на 7 подучается в частном нуль, то это означает, что взятый год в колонне первой таблицы занимает, по своему положению, последнее или седьмое место сверху; поэтому такие нули нужно считать равными семи. Для 1899 г. при остатке 18 (от. деления его на 19) имеем (18: 3 = 6 + 0; 46 —18 = 28:7 = 4+) 0, каковой и считаем за 7.

Если остаток меньше 7, тогда, очевидно, избранный год занимает в первой вертикальной колонне слева таблица I то место, сколько показывает цифра остатка; понятно, что в таких случаях деление на 7 производить не нужно, а следует просто запоминать для Г самый остаток В. Для 1904-го года, при остатке (от деления на 19) 4, имеет (4 + 10=14; 46 — 14 = 32 — 30 =) 2; эта последняя цифра (2) будет служить и для В и для Г.

Д) Остаток от деления года на 28 увеличиваем столькими единицами, сколько раз в нем содержится 4. 1895 г. : 28 = 67 + 19:4 = 4+3. Поэтому 19+4 = 23.

Если этот остаток равняется нулю или меньше 5 (не больше 4), то никаких прибавок не делается, ибо самый остаток уже показывает положение взятого года в первой колонне снизу второй таблицы. Для годов с 1904 по 1908 от деления на 28 получаем 0. 1. 2. 3. 4.

411

E) Найденное число делим 7 и отмечаем остаток. Для 1895 г. получает (23:7 = 3+) 2.Для 1911 г. имеем (1911 : 28 = 68 + 7; 7:4=1+ 3; 7 + 1 = 8; 8:7 = 1+) 1.

Если число Д меньше 7, то деление не производится, ибо для такого года положением будет в первой колонне второй таблицы то место, сколько обозначает число Д. Для годов с 1904 по 1908 имеем 0. 1. 2. 3. 4. Для 1909 г. получим (1909:28 = 68 + 5; 5 :4 = 1 + 1; поэтому 5 + 1 =)6.

Если от деления этого числа на 7 получится 0, то значит взятый год равняется седьмому месту в колонне второй таблицы; потому 0 = 7. Так, (1899-й г.) : 28 = 67 + 23 : 4 = 5 + 3; 23 + 5 = 28 : 7 = 4 + 0; отсюда 0 = 7.

Ж) Числа Г и Е слагаем и вычитаем из 7. Для 1894 г. Г = (1894 : 19 = 99 + 13; 13:3 = 4 + 1; 13+10 = 23; 46 — 23.= 23 : 7 = 3 + ) 2и Е = (1894 : 28 = 67 + 18; 18:4 = 4+2; 18 + 4 = 22 : 7 = 3+) 1. Поэтому Ж(2 + 1=3; 7 — 3) = 4.

Если сумма Г и Е больше 7, то ее следует вычитать из 14-ти. Напр., для 1890 г. Г и Е = 0 и 3 или 7 + 3 = 10; 14—10=4.

З) Это число приложим к цифре В и, если сумма больше 10, вычитаем из нее 10: тогда и будет для пасхи число апреля. Для 1895 г. В= 12, а Ж=(1895:28 = 67 + 19; 19: 4 = 4 + 3; 19+4= 23:7=3 + 2; 5+ 2 = 7; 7 —7=) 0. 12 + 0=12 —10 = 2. Пасха будет второго апреля. Для 1890 года Ж равняется 4, а З— (7 + 4 =)11; пасха была (11— 10=) 1-го апреля.

Если сумма Ж и З меньше 10, то ясно, что пасха от первого пункта пасхального предела не подвинулась за границу парта (21+10= тридцать одному дню марта); в таком случае к этой сумме нужно прибавить 21 и результат укажет для пасхи соответствующее число марта. Возьмем 1877-и год. В = (1877:19 = 98+15; 46 — 15 = 31 — 30 = ) 1. Г=1. Е= (1877:28 = 67+) 1. Ж = (1+ 1 = 2; 7 — 2 = ) 5. Ж +

412

В = (5+1=) 6; 6 + 21 = 27. Пасха в 1877 году была 27-го марта.

Приведен теперь для иллюстрации, по примеру на каждый случай.

1) Случай—наиболее правильный: 1894-й год. Остатки его 13 и 18. В = (13:3 = 4+1; 13+10 = 23; 46 — 23 = ) 23. Г=(23:7 = 3+) 2. Е= (18:4 = 4 + 2; 18+4 = 22 : 7=3+) 1. Ж = (2 + 1 = 3; 7 —3 = ) 4. 23 + 4= 27—10 = 17—ое апреля.

2) 1900-й год. Остатки 0 и 24. В =[46 = (0 + 30 = )] 16. Г=(16:7 = 2 + ) 2. Е=(24:4 = 6; 24 + 6 = 30 : 7 = 4+) 2. Ж = (2 + 2= 4; 7 —4 = ) 3. Пасха = (16 + 3 = 19—10) 9-го апреля. 1901-й год. Остатки 1 и 25. В = [46 — (1 + 10 = ) 35 — 30 = ] 5. Г=5. Е=(25 : 4 = 6 + 1; 25 + 6 = 31:7 =4 + ) 3. Ж = (5 + 3 =8; 14 — 8=) 6. Пасха будет=(5+6 = 11 — 10) 1-го апреля. 1902-й год. Остатки 2 и 26. В = [46—(2 + 20 = )] 24. Г = (24 : 7 = 3+) 3. Е = (26 : 4 = 6 + 2; 26 + 6 = 32 : 7 = 4 +) 4. Ж = (3 + 4= 7; 7—7 = ) 0. Пасха будет (24 — 10 =) 14-го апреля.

3) 1903-й год. Остатки 3 и 27. В = (46 — 3 = 43 — 30 = ) 13. Г=(13 :7 = l+) 6. Е = (27 : 4 = 6+3; 27 + 6= 33 : 7 = 4+) 5. Ж = (6 + 5=11; 14 — 11=) 3. 13 + 3=16 — 10 = 6; т. е. пасха 6-го апреля.

4) 1899-й год. Остатки 18 и 23. В = (18 : 3 = 6; 46 — 18 = ) 28. Г = (28 : 7 = 4+) 0 или 7. Е = (23 : 4 = 5 + 3; 23 + 5 = 28:7 = 4+) 0 или 7. Ж = (7 н-7 = 14— 14 = ) 0. 28—10 = 18-му апреля, когда и будет пасха.

5) 1904-й год. Остатки 4 и 0. В = (4 : 3 = 1 + 1; 4 + 10 = 14; 46 —14 = 32 —30 =) 2. Г=2. Е = 0. Ж=(2 + 0 = 2; 7 — 2=) 5. 2 + 5 = 7 + 21 = 28-ое марта, на которое и упадет пасха.

6) 1909-й год. Остатки 9 и 5. В = (9 : 3 = 3 + 0; 46 — 9 = 37 — 30 =) 7. Г=(7 : 7= 1 +) 0 или 7. Е = (5 :4 = 1 +1;

413

5 + 1=) 6. Ж= (7+6 = 13; 14 — 13=) 1. 7 + 1 = 8 + 21 = 29-му марта, когда и придется пасха.

7) 1915-й год. Остатки 15 и 11. В = (46 — 15 = 31 — 30=) 1. Г= 1. Е=(11:4=2 + 3; 11+2=3:7=1+) 6. Ж=(1 + 6 = 7; 7 — 7 = ) 0. 1 + 0 = 1 +  21 = 22; пасха будет 22-го марта. 1885-й год. Остатки 4 и 9. В = (4:3 = 1 + 1; 4 + 10 = 14; 46 — 14 = 32 — 30=) 2. Г = 2. Е = (9:4 = 2 + 1; 9 + 2 = 11: 7 = 1 +) 4. Ж = (2 + 4=6; 7— 6 = ) 1. 2 + 1 = 3 + 21 = 24; пасха приходилась 24-го марта.

Всю процедуру, как она изложена выше, можно несколько видоизменить и, пожалуй, упростить. Тогда получится второй способ для отыскания дня празднования св. пасхи в каном угодно году. Все действия будут располагаться в следующем порядке.

а) Избранный год разделить на 28 и к поименному остатку прибавить содержащееся количество четверок; эту сумму затем разделить на 7 и остаток (какой бы он ни был,—даже если нуль) вычесть из семи и разницу запомнить. Напр. 1916 год. 1916 : 28 = 68 + 12; 12:4 = 3; 12 + 3=15; 15:7 = 2 + 1; 7 — 1 = 6.

Если остаток от деления года на 28 меньше 4, то его нужно прямо вычитать из семи и замечать эту разницу. Для 1904 она будет равняться (1904 : 28 = 68 + 0. 7 — 0 = ) 7. Для 1907 г. она = (1907 : 28= 68 + 3. 7 — 3 = ) 4.

Если остаток от деления года на 28, увеличенный количеством содержащихся в нем четверок, будет меньше 7, то его нужно прямо вычитать из семи. Для 1908 г. будет иметь (1908 : 28 = 68 + 4; 4:4 = 1; 4 + 1=5; 7—5=) 2. Для 1909 г. подучится (1909 : 28 = 68 + 5; 5 : 4=1 + 1; 5 + 1=6; 7—6=) 1.

Если остаток от деления года на 28, увеличенный соответствующим количеством четверок, — после деления его на 7— даст нуль, то этот нуль и вычитать из 7. Для 1910 г. имеем (1910 : 28 = 68 + 6; 6 : 4 = 1 + 2; 6 + 1 = 7; 7 : 7 = 1 + 0; 7—0=) 7.

414

β) Тот же избранный год разделить на 19 и остаток увеличить стольники десятками, сколько единиц получится в остатке от деления его на 3, и сумму вычесть из 16. Если этот остаток на три делится на цело или меньше трех (т. е. 0. 1 и 2), то нужно вычитать прямо его; если по вычитании разница будет равна 30 или больше 30, то вычесть еще 30. Для 1916 г. имеем (1916 : 19 = 100 + 16; 16 : 3=5 +1; 16 + 10 =26; 46 —26 =) 20. Для 1918 имеем (1918 : 19 = 100 + 18; 18 : 3 = 6 + 0; 46—18 =) 28. Для 1902 г. имеем (1902 : 19 = 100 + 2; 46—2 = 44; 44— 30 =) 14. Для 1904 г. получится (1904 : 19 = 100 + 4; 4 : 3 = 1 + 1; 4 + 10=14; 46—14 = 32; 32—30=) 2.

γ) Если последняя разница меньше 7 и разницы а или равна ей, то последнюю (а) прибавить к 21—и в сумме получим для пасхи соответствующее число марта. Для 1942 г. а = (1942 : 28 = 69 + 10; 10:4 = 2 + 2; 10 + 2 = 12; 12 : 7 = 1 + 5; 7—5 = ) 2; γ=(1942 : 19= 102 + 4; 4 : 3 = 1 + 1; 4 + 10= 14; 46—14 = 32 —30 =) 2. γ или 2 а или 2; потому 21 + 2= 23. Пасха в 1942 г. будет 28-го марта.

δ) Если разница β больше α, то к α нужно прибавить столько семерок, сколько раз 7 содержится в γ; сумму прибавить к 21.

Если получится цифра меньше 31, она будет обозначать для пасхи число марта; если больше 31, вычесть из нее 31 — и получим для пасхи число апреля. Для 1909 г. имеет: α= (1909 : 28 = 68 + 5; 5 : 4 = 1 + 1 ; 5 + 1 = 6; 7—6=) 1, β =(1909 : 19  100 + 9; 9 : 3 = 3 + 0; 36 — 9= 37 — 30 = 7; 7 : 7= 1 + 0; 7 X 1 = )7. α + β или 1 + 7 = 8; 21 + 8 = 29; пасха будет 29-го марта. Для 1905 года получаем: α = (1905 : 28 = 68 + 1; 7—1 = ) 6; β = (1905: 19 ==100 + 5; 5 : 3 = 1 + 2; 5 + 20 = 25. 46—25 = 21 : 7 = 3 + 0; 7 Х 3=)21. 6 + 21 = 27 + 21 = 48—31=17; пасха в 1905 году будет 17-го апреля.

415

В заключение предлагаем анализ двух примеров для крайних сроков, когда вообще бывает пасха, т. е. для 22-го марта и для 25-го апреля.

Для первого случая можно взять 1915 г. Для него получаем: α = (1915 : 28 = 68 +11 : 4 = 2  + 3; 11 + 2=13: 7=1 + 6; 7 — 6 = ) 1; β = (1915 : 19 = 100 + 15; 15 : 3 = 5 + 0; 46—15=31 — 30 = ) 1. 21 + 1=22; пасха в 1915 г. случится 22-го марта.

Для второго случая возьмем 2800 г. Для него имеет: α = (2800 : 28 = 100 + 0; 7 — 0 = ) 7; β = (2800 : 19 = 147 + 7; 7 : 3 = 2 + 1; 7 + 10 = 17; 46 — 17 = 29: 7 = 4 + 1; 7 X 4=) 28. 7 + 28 = 35; 21 + 35 =57 — 31 = 25; это показывает, что пасха в 2800 г. будет 25-го апреля.

Но само собою понятно, что все разобранные вами способа не дают еще всего, что может потребоваться в хронологических изысканиях для практических и научных целей. Поэтому присоединяем обозрение общедоступных пособий по хронологии в русской литературе.

Хорошее руководство по   этому предмету представляет книга г. Г. М. «Времясчисление у древних и новых народов» (Казань, 1884 г. II + 96 стр. Цена 75 к.). Здесь автор дает сжатое обозрение календарей и эр у разных народов и затем (гл. III) внимательно излагает «русское летосчисление», чего нет в переводном труде (1867 г.) Лалоша «Времясчисление христианского и языческого мира». Последняя (IV) глава посвящена подробному учению о «православной пасхалии» и дает все нужные—научные, исторические и церковные—сведения. В приложениях находим «Пасхальный круг с обозначением годов XI, ХIII и XIV (текущего) индиктионов», «Таблицу лунного течения», «Пасхалию зрячую по ключевым буквам» с расписанием подвижных праздников, «Указатель дней недели, в которые приходятся 1, 8, 15, 22 и 29 числа каждого месяца в мартовском, сентябрьском и январском годах простых и високосных, на все числа, в которые бывает св. пасха, т. е.

416

с 22 марта по 25 апреля», «Таблицу для нахождения дней недели, соответствующих данным числам месяцев в текущем и прошлом столетиях, обнимающих период русской истории» и «Перевод мартовских и сентябрьских годов по январским».

Изучив эту книгу, каждый без особенного труда сделает все нужные ему вычисления. Но само собою понятно, что для этого необходимы некоторые познания и математическая опытность, между тем далеко не все обладают такими качествами, а иногда хронологические справки требуются быстро. Для таких лиц можно порекомендовать «Справочный табличный календарь с пасхалией на все годы по православному летосчислению (старому стилю», составленный по православной пасхалии священником виленской дворцовой церкви Капитоном Петровым (Вильна 1887. Цена 25 коп.). Это небольшая книжка в 14 листиков с двумя указателями и ΧΙV таблицами, которые — для удобства пользования—полно наклеить на картон или полотно:—тогда «календарь» будет стенным. Для употребления его нужно только умение разделить избранные год на 28 или 19 и произвести самое простое вычитание, и затем он покажет а) число пасхи в каком угодно году и зависящие от нее праздники и поста (недели, подготовительные к посту, Вербное воскресение, Вознесение, Пятидесятницу, продолжительность Петрова поста и пр.) и б) во всех годах от Сотворения Мира до Рождества Христова и после него—1) день недели, когда известны год, месяц и число, 2) числа месяца, когда знаем год, месяц и день и 3) месяц, когда даны год, число и день. Книжка эта весьма практична и пригодна «для исторических, юридических и семейных справок». Вся процедура занимает не более двух-трех кинут, но показания ее безусловно верны.

Для тех, кто стесняется даже первыми арифметическими действиями или тяготится обращаться к помощи карандаша, очень пригоден «Общедоступный вечный календарь» (Харьков, 1891 г., цена с перес. 40 коп.). Он состоит из трех таблиц. Таблица I—«для определения дней недели, соответствующих числам

417

месяцев» в годах от сотворения мира и по Рождестве Христовом, а для русской истории—в годах мартовских (кончая 7000-м от сотв. мира) и в сентябрьских (с 7001 до 7203-го от сотв. мира). По этой таблице можно узнать: 1) день недели по году и числу, 2) по тем же данным распределение чисел всех месяцев по дням недели и 3) то, в какие годы бывает совпадение такого-то числа месяца с известным днем, напр. 1-го апреля с воскресеньем, 1-го февраля с пятницей и т. п. Таблица II—«для отыскания дней празднования Пасхи»— представляет собственно пасхальные полнолуния, но праздник Воскресения Христова находится легко и безошибочно. Таблица III показывает распределение постов, мясоедов а подвижных праздников соответственно числу дня св. пасхи в избранном году. На отдельном листке приложен «карманный календарик на 200 лет» (с 1800 до 2000 года) для распределения чисел взятого года по дням недели.

Рассмотренный нами «Общедоступный вечный календарь» составлен применительно к данным г. Г. М. (хотя, колет быть, и независимо от него) и вполне удовлетворяет своим целям.

Еще большее упрощение представляет остроумный и оригинальный способ, предложенный в 1891 г. на страницах московского иллюстрированного журнала «Наука и Жизнь». Это крестообразная таблица; в верхней части — цифры столетий юлианского и грегорианского календарей, внизу — десятки я единицы, справа—месяцы, слева — числа. В средине подвижной кружок с обозначением дней недели. Сто́ит только сделать три поворота этого кружка,—и по данным числа месяца и года легко находится соответствующий им день недели.

Этот календарь отвечает только на один вопрос, но преимущества его те, что он упрощен до minimum’а и принимает во внимание летосчисление грегорианское, чего в других нет.

На том же принципе возможной простоты, но в более широком масштабе построен выпущенный в 1891 г. в Москве

418

«Полный общедоступный стенной календарь старого и нового стилей с вечной пасхалией православной церкви» г. Г. Иоффе (цена с пересылкой 1 р. 20 коп.). Это большой плотный пергаментный лист, на котором четко и в несколько красок отпечатаны «Вечный календарь», «Вечная пасхалия православной церкви» со «вспомогательною таблицей» и табель «переходящих праздников, сплошных седмиц, постов и дней поминовения, зависящих от пасхи». На полях и на оборотной стороне помещены необходимые разъяснения и «научные заметки». Для пользования точно так же нужно передвигать соответственные полоски, пластинки и кружки. При помощи этих несложных манипуляций «Вечный календарь» указывает 1) дни недели по году и числу и 2) годы — по дню в известное число данного месяца. «Вечная пасхалия» с табелем показывает пасху и преходящие праздники, а по дню пасхи взятого года—число и день события до или после нее; по ним же обратно можно находить годы для известных комбинаций праздников, напр.: когда Кирио-Пасха (т. е. Светлое Воскресение) совпадает с Благовещением, 25-м марта, или когда Вознесение упадает на 9-ое мая, день св. Николая Чудотворца и т. д.? Можно также «календарь» поставить в начале года, и он будет служить в течение его по всем отмеченным вопросам.

Отсюда видно, что труд г. Иоффе «дает календарные справки и ответы на всякие вопросы, прямые и обратные, относительно постоянных и преходящих праздников, дней повиновения, табельных дней и т. п. в прошедшем, настоящем и будущем времени». Все эти сведения—при небольшом навыке—получаются легко, скоро и удобно без всяких вычислений, а потому «Календарь» г. Иоффе пригоден для всех грамотных людей и может быть полезен для научных и практических целей. Научное его достоинство было признано физико-математическою комиссией, которая дала одобрительный отзыв. (См. ΙV-й том «Трудов отделения физических наук Императорского Общества любителей естествознания», Москва 1891 г.).

С своей стороны мы могли бы прибавить, что для полноты

419

дела не излишне бывает знание пасхалии по грегорианскому новому стилю, чего нет ни в одном из разобранных пособии. Для многих и не редко это бывает нужно.

Для этой цели могут служить прекрасные рассуждения г. Перевощикова («Правила времясчисления, принятого православною церковью». Москва 1850 г.) и прот. П. С. Делицына, проф. Моск. дух. академии («Способ находить в данном году день святой Христовой пасхи у христиан как православных, так и западных» в «Чтениях в Московском обществе любителей духовного просвещения» за 1865 г.), которые дают также и обозрение православного времясчисления вообще; ими и мы пользовались в начале статьи. Еще подробнее все хронологические вопросы разбираются в изданной в С.-Петербурге в 1879 году книге покойного профессора новороссийского университета В. И. Лапшина под заглавием «Лунное течение и разные способы определения пасхи православной и западной» (XVI + 83 стран., цена 25 коп. с пересылкой вместо номинальных 75 коп.), хотя изложение иногда несколько запутанно. Как видно отсюда, автор сосредоточивается на частном вопросе, но исследует его довольно обстоятельно и с научной точки зрения и с практической стороны. Сочинение распадается на шесть отделов. В первом (§§-фы 1—15) приводятся общие сведения о пасхе, годах, движении луны и другие необходимые данные, а тем подробно сообщается о приспособленном г. Лапшиным «приборе лунного течения» для определения Светлого Воскресения и зависящих от него дней; он отпечатан на особом листе и легко может быть приноровлен для практического пользования. Во второй части описываются разные старенные «лунники» по книге В. Срезневского «Северный резной календарь», Magnusson’a Description ofа Norwegian clog Calendar (Cambridge, 1879), Следованной Псалтири 1686 г., «Руке Богословлей» (Москва, 1787) и рукописи Императорской публичной библиотеки № 199 (§§-фы 16—21); рассуждения автора иллюстрируются и здесь точными чертежами в приложении. В отделах 3, 4 и 5 (§§-фы 22—38) приводятся разные способы определения Пасхи, напр. посредством неопределенных

420

уравнений с двумя неизвестными, по формуле проф. А. Н. Савича и т. п., и учение о пасхальных элементах (эпакта, основание, вруцелето, ключ границ), где указано «приложение счисления к поверке данных хронологических в русских летописях». В конце (§§-фы 39—13) обсуждается вопрос о пасхе по грегорианскому календарю; он разобран менее подробно, но настолько удовлетворительно, что сущность дела понятна,— особенно в виду того, что изложение приспособляется к православным пасхальным терминам.

Н. Г.