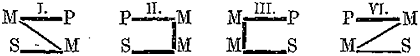Челпанов Г., проф. Учебник логики

ПРЕДИСЛОВИЕ.

В настоящем учебнике Логики «силлогистике» уделено больше места, чем это следовало бы по представлению современного читателя, для которого силлогистика есть символ старой схоластической логики. Поэтому может показаться, что я в своей книге предлагаю возвратиться ко временам схоластики. Но пренебрежительный взгляд на силлогистику является одним из предрассудков, мешающих распространению у нас такой важной научной дисциплины, как логика. Не говоря уже о том, что без силлогистики понятие умозаключения было бы неясным и индуктивная логика оставалась бы совершенно непонятной, изучение силлогистики является чрезвычайно важным для умственного развития учащихся. Образовательное значение ее основывается на том, что учащийся, знакомясь с разнообразными формами дедуктивного умозаключения, научается более умело обращаться с собственной мыслью. В этом заключается практическая важность логики, как образовательного предмета.

Но изучение логики отнюдь не должно ограничивается теоретическим изучением правил, изложенных в учебнике. Истинное знание логики предполагает не только знакомство с правилами логики, но и умение их применять. Поэтому необходимо, чтобы при изучении логики учащийся упражнялся в практическом применении логических правил. Только в том случае, если он на примерах самостоятельно рассмотрит применение тех или других правил, изучение логики может оказаться целесообразным. Для этой цели в учебнике помещены задачи, которые учащийся обязан решить. Задачи преднамеренно избраны легкие, вполне доступные для начинающего. Если же кто-либо из учащихся пожелает

VII

 

 

испробовать свои силы на более трудных задачах, то он найдет богатый и разнообразный подбор их в приложении к логике Минто, сделанном переводчиками этой книги A. С. Белкиным и H. В. Ивановским, а также в книге Н. О. Лосского «Сборник элементарных упражнений по логике». Спб. 1908.

Предисловие к 3-му изданию,

В настоящем издании частичные поправки введены почти во все главы и прибавлены некоторые задачи. Главы и параграфы, обозначенные звездочками или отделенные скобками, могут быть пропущены при изучении учебника в гимназии.

Предисловие к 4-му изданию.

В настоящем издания прибавлено около 150 задач. Большинство этих задач придумано слушательницами Московских Высших Женских Курсов. Я бы желал, чтобы это послужило доказательством того, что учащиеся могут не только решать задачи, но и самостоятельно придумывать таковые.

Автор.

VIII

 

 

ГЛАВА 1-я.

Определение и задачи логики.

Определение логики. Для того чтобы определить, что такое логика, мы должны предварительно выяснить, в чем заключается цель человеческого познания. Цель познания заключается в достижении истины при помощи мышления, цель познания ест истина. Логика же есть наука, которая показывает, как должно совершаться мышление, чтобы была достигнута истина; каким правилам мышление должно подчиняться для того, чтобы была достигнута истина. При помощи мышления истина иногда достигается, а иногда не достигается. То мышление, при помощи которого достигается истина, должно быть названо правильным мышлением. Таким образом логика может быть определена как наука о законах правильного мышления, или наука о законах, которым подчиняется правильное мышление.

Из этого определения видно, что логика исследует законы мышления. Но так как исследование законов мышления, как известного класса психических процессов, является также предметом психологии, то предмет логики выяснится лучше в том случае, если мы рассмотрим отличие логики от психологии в исследовании законов мышления.

Психология и логика. На мышление мы можем смотреть с двух точек зрения. Мы можем на него смотреть прежде всего как на известный процесс, законы которого мы исследуем. Это будет точка зрения психологическая. Психология описывает, как совершается процесс мышления. С другой стороны, мы можем смотреть на мышление как на средство достижения истины. Эта цель может достигаться, может и не достигаться. Логика исследует, каким законам должно подчиняться мышление, чтобы оно могло привести н истине.

Итак, разкица между психологией и логикой в отношении к процессу мыишгения может быть выражена следующим

1

 

 

образом. Психология рассматривает мышление так, как оно есть; логика так, как оно должно быть. Психология рассматривает безразлично всевозможные роды мыслительной деятельности: рассуждение гения, бред больного, мыслительный процесс ребенка, животного—для психологии представляют одинаковый интерес, потому что она рассматривает только, как осуществляется процесс мышления; логика же рассматривает условия, при которых мысль может быть истинной, достоверной. В этом отношении логика сближается с этикой, или наукой о нравственности, и с грамматикой. Подобному тому, как этика указывает законы, которым должна подчиняться наша жизнь, чтобы быть добродетельной, и грамматика указывает правила, которым должна подчиняться речь, чтобы быть правильной, так логика указывает нам правила, законы или нормы, которым должно подчиняться наше мышление для того, чтобы быть истинным. (Норма от латинского слова norma—есть правило, которое показывает, как что-либо должно совершаться.)

Психология есть наука описательная, потому что она описывает и объясняет, как совершаются в действительности умственные процессы; логика есть наука нормативная, потому что она указывает те нормы, которым мышление должно подчиняться.

Для того, чтобы понять утверждение, что существуют известные правила, которым должно подчиняться мышление, рассмотрим, в чем заключается задача логики.

Задача логики. Есть положения или факты, истинность которых усматривается непосредственно, и есть положения и факты, истинность которых усматривается посредственно, именно через посредство других положений или фактов. Если я скажу: «я голоден», «я слышу звук», «я ощущаю тяжесть», «я вижу, что этот предмет большой», «я вижу, что этот предмет движется» и т. п., то я выражу факты, которые должны считаться непосредственно познаваемыми. Такого рода факты мы можем назвать также непосредственно очевидными, потому что они не нуждаются ни в каком доказательстве: их истинность очевидна без доказательств. В самом деле, разве я нуждаюсь в доказательстве, что передо мною находится предмет, имеющий зеленый цвет; неужели, если бы кто-нибудь стал доказы-

2

 

 

вать, что этот предмет не зеленый, а черный, я поверил бы ему? Этот факт для меня непосредственно очевиден. К числу непосредственно очевидных положений относятся прежде всего те положения, которые являются результатом чувственного восприятия, а также и внутреннего опыта, напр.: «это воспоминание для меня неприятно». К непосредственно очевидным положениям относятся также математические аксиомы и определения.

Все те факты, которые совершаются в нашем отсутствии (например, прошедшие явления, а также и будущие), могут быть познаваемы только посредственно. Я вижу, что дождь идет,—это есть факт непосредственного познания; что ночью шел дождь, есть факт посредственного познания, потому что я об этом узнаю через посредство другого факта, именно того факта, что почва мокрая. Факты посредственного познания или просто посредственное познание является результатом умозаключения, вывода. По развалинам я умозаключаю, что здесь был город. Если бы я тысячу лет тому назад был на этом месте, то я непосредственно воспринял бы этот город. По следам я заключаю, что здесь проехал всадник. Если бы я был здесь час тому назад, то я непосредственно воспринял бы самого всадника.

Посредственное знание доказывается, делается убедительным, очевидным при помощи знаний непосредственных. Этот последний процесс называется доказательством.

Таким образом есть положения, которые не нуждаются в доказательствах, и есть положения, которые нуждаются в доказательствах и очевидность которых усматривается посредственно, косвенно.

Если есть положения, которые нуждаются в доказательствах, то в чем же заключается доказательство? Доказательство заключается в том, что мы положения неочевидные стараемся свести к положениям или фактам непосредственно очевидным или вообще очевидным. Такого рода сведение положений неочевидных к положениям очевидным лучше всего можно видеть на доказательствах математических. Если возьмем, например, теорему Пифагора, то она на первый взгляд совсем не очевидна. Но если мы станем ее доказывать, то, переходя от одного положения к другому, мы придем в конце концов к аксиомам и определениям, которые имеют не-

3

 

 

посредственно очевидный характер. Тогда и самая теорема сделается для нас очевидной.

Таким образом познание посредственное нуждается в доказательствах; познание непосредственное в доказательствах не нуждается и служит основой для доказательства познаний посредственных.

Заметивши такое отношение между положениями посредственно очевидными и положениями непосредственно очевидными, мы можем понять задачи логики. Когда мы доказываем что-либо, т.-е. когда мы сводим неочевидные положения к непосредственно очевидным, то в этом процессе сведения мы можем сделать ошибку: наше умозаключение может быть ошибочным. Но существуют определенные правила, которые показывают, как отличить умозаключения правильные от умозаключений ошибочных. Эти правила указывает логика. Задача логики поэтому заключается в том, чтобы показать, каким правилам должно следовать умозаключение, чтобы оно было правильным. Если мы эти правила знаем, то мы можем определить, соблюдены ли они в том или другом процессе умозаключения.

Из такого определения задач логики можно понять значение логики.

Значение и польза логики. Для выяснения значения логики обыкновенно принято исходить из определения ее. Мы видели, что логика определяется как наука о законах правильного мышления. Из этого определения логики, по-видимому, следует, что стоит изучить законы правильного мышления и применять их в процессе мышления, чтобы можно было мыслить вполне правильно. Многим даже кажется, что логика может указывать средства для открытия истины в различных областях знания.

Но в действительности это неверно. Логика не поставляет своею целью открытие истин, а ставит своею целью доказательство уже открытых истин. Логика указывает правила, при помощи которых могут быть открыты ошибки. Вследствие этого, благодаря логике можно избежать ошибок. Поэтому становится понятным утверждение английского философа Д. С. Милля, что польза логики главным образом отрицательная. Ее задача заключается в том, чтобы предостеречь от  возможных ошибок. Вслед-

4

 

 

ствие этого практическая важность логики чрезвычайно велика. «Когда я принимаю в соображение,—говорит Д. С. Милль,— как проста теория умозаключения, какого небольшого времени достаточно для приобретения полного знания ее принципов и правил и даже значительной опытности в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься с успехом каким-нибудь умственным трудом, упускает это изучение. Логика есть великий преследователь темного и запутанного мышления; она рассеивает туман, скрывающий от нас наше невежество и заставляющий нас думать, что мы понимаем предмет в то время, когда мы его не понимаем. Я убежден, что в современном воспитании ничто не приносит большей пользы для выработки точных мыслителей, остающихся верными смыслу слов и предложений и находящихся постоянно настороже против терминов неопределенных и двусмысленных, как логика».

Многие часто ссылаются на так называемый «здравый смысл» и говорят: «да, ведь, ошибки можно открывать без помощи логики, посредством лишь одного здравого смысла». Это, конечно, справедливо, но часто бывает недостаточно найти ошибку, нужно бывает объяснить ее, уметь точно характеризовать ее и даже обозначить ее. Иной знает, что в том или другом умозаключении есть ошибка, но он не в состоянии сказать, почему это умозаключение нужно считать ошибочным. Это часто возможно сделать только благодаря знанию правил логики.

Логика имеет также значение для определения взаимного отношения между науками. Различие между науками, например, математическими, физическими и историческими, может сделаться ясным только в том случае, если мы рассмотрим различие методов познания с логической точки зрения.

История логики и главное направление ее. Творцом логики, как науки, следует считать Аристотеля (384—322). Логика Аристотеля имела господствующее значение не только в древности, но также и в средние века, в эпоху так называемой схоластической философии. Заслуживает упоминания сочинение последователей философа Декарта (1596—1650), которое называлось La logiqueou l’art depenser (1662). Эта логика, которая называется логикой Port Royale, принадлежит к так называемому формальному направлению. В Англии

5

 

 

Бэкон (1561 — 1626) считается основателем особого направления в логике, которое называется индуктивным, наилучшими выразителями которого в современной логике являются Д. С. Милль (1806—1873) и А. Бэн (1818—1903). Объединителями обоих этих направлений следует считать Джевонса (1835—1888), Зигварта (1830—1904) и Вундта (род. 1832).

Для того, чтобы понять, в чем заключается различие между формальным и индуктивным направлением в логике, заметим, что называется материальной и формальной истинностью. Мы считаем какое-либо положение истинным материально, когда оно соответствует действительности или вещам. Мы считаем то или другое заключение истинным формально в том случае, когда оно выводится с достоверностью из тех или иных положений, т.-е. когда верен способ  соединения мыслей, самое же заключение может совсем не соответствовать действительности. Для объяснения различия между формальной и материальной истинностью возьмем примеры.

Нам даются два положения:

Все вулканы суть горы

Все гейзеры суть вулканы.

Из этих двух положений с необходимостью следует, что «все гейзеры суть горы». Это заключение формально истинно, потому что оно с необходимостью следует из двух данных положений, но материально оно ложно, потому что оно не соответствует действительности: гейзеры н е суть горы. Таким образом умозаключение истинное формально может быть ложным материально.

Но возьмем следующий пример:

Все богачи тщеславны

Некоторые люди не суть богачи

След., некоторые люди не суть тщеславны.

Это заключение истинно материально, потому что действительно «некоторые люди не суть тщеславны», но оно формально ложно, потому что не вытекает из данных положений. В самом деле, если бы было сказано, что только богачи тщеславны, тогда о всяком не-богаче мы сказали бы, что он не тщеславен. Но у нас в первом положении утверждается: «все богачи тщеславны»; этим не исключается, что и другие люди могут быть тщеславными. В таком слу-

6

 

 

чае можно быть небогатым и в то же время быть тщеславным; из того, что кто-нибудь не есть богач, не следует, что он не может быть тщеславным. Из этого ясно, что указанное заключение не вытекает из данных положений необходимо.

Те правила, которые указывают, когда получаются заключения истинные формально, мы можем назвать формальными критериями истинности; те правила, которые определяют материальную истинность, мы можем назвать материальными критериями истинности.

Формальная логика по преимуществу изучает те отделы логики, в которых может быть применяем формальный критерии истинности. Индуктивная логика, в противоположность формальной логике, по преимуществу разрабатывает те отделы, в которых применяется материальный критерий.

Вопросы для повторения. Как определяется логика? Какое различие существует между психологией и логикой? Какие положения нужно считать непосредственно очевидными? Какие положения нужно считать посредственно очевидными? В чем заключается задача доказательства? В чем заключается задача логики? Почему „здравый смысл“ не может заменить логики? Какие существуют основные направления в логике? Что такое формальная истинность и что такое материальная истинность? Что такое формальный и материальный критерий истинности? Какое различие между формальной и индуктивной логикой?

 

Г Л A В А 2-я.

О реальности понятий.

О реальности понятий. В Психологии мы видели, что понятиями называются такие умственные построения, которые относятся к классу, к группе однородных вещей. Мы обладаем известными понятиями, но спрашивается, существует ли какая-либо реальность, которая соответствовала бы нашим понятиям? Вопрос о существовании реальности, соответствующей нашим понятиям, имеет следующее основание. Когда мы имеем представление этого стола, этого дома, этого человека, то мы говорим, что ему во внешнем мире соответствует известная единичная вещь. Если это так, то можно поставить вопрос: а что же соответствует нашему понятию стола, понятию дома, понятию человека? Ведь ни-

7

 

 

чего не соответствовать не может, потому что в таком случае понятия в нашем уме были бы фикциями, т.-е. мы мыслили бы что-то, чему не соответствует ничего реального; у нас в уме было бы понятие человека, но никакой реальности, соответствующей этому понятию, не было бы. Из этого ясно, что вопрос о реальностях, соответствующих нашим понятиям, имеет известное основание.

Рассмотрим вкратце историю вопроса о реальности понятий.

Платон (427—347) признавал объективно-реальное существование понятий, которые он называл идеями. В мире, подлежащем нашему чувственному восприятию, существует этот, другой, третий стол; но кроме этих единичных столов в мире сверхчувственном существует еще идея стола, соответствующая нашему понятию стола. Истинное существование присуще только вещам мира сверхчувственного, за небесного, чувственный же мир, который мы воспринимаем при помощи наших органов чувств, есть только тусклое отражение мира идей. В то время как чувственные вещи представляют нечто скоропреходящее, постоянно изменяющееся, идеи представляют собою нечто вечное и неизменное. Итак, по Платону, понятиям в нашем уме соответствуют те идеи, которые реально существуют в форме вещей, в мире сверхчувственном.

Аристотель, ученик Платона, соглашается с ним в том, что идеи, как их понимал Платон, действительно существуют реально, но он не находит никаких оснований для допущения, что идеи существуют отдельно от чувственно воспринимаемых вещей. То общее, что является предметом понятия, находится в единичных вещах, оно как бы распределяется между единичными вещами.

Таким образом, по Платону, идеи или понятия существуют отдельно от вещей; по Аристотелю, они существуют в самих вещах. Но и по Платону, и по Аристотелю, понятия существуют реально. Поэтому Платон и Аристотель называются реалистами.

В средние века вопрос о реальности понятий появился в новой форме. Назывался он вопросом об универсалиях; универсалии и суть общие представления, понятия, идеи, о реальности которых шла речь. Средневековые философы решали этот вопрос двояко.

8

 

 

Одни говорили: «universalia sunt realia». Для них идеи, понятия, универсалии были реальностью, т.-е., по их мнению, кроме единичных вещей, предметов чувственного восприятия, существуют еще и идеи. Это учение называлось реализмом.

Другие утверждали: «universalia sunt nomina»; понятия, общие представления реально не существуют; они суть только умственные построения, которые обозначаются при помощи одного и того же имени; они суть собственно имена, обозначающие собрание или совокупность сходных единичных вещей. Для этих философов реальны только единичные вещи, универсалии же—не больше, как простые названия, имена (nomina). Это учение называлось номинализмом.

Таким образом к концу средних веков по занимающему нас вопросу мы находим две школы: реалистическую, признававшую реальность понятий или идей, и номиналистическую, отрицавшую эту реальность.

В номинализме выделяется одна школа, которая признавала реальность понятий или общих представлений в нашем уме, и ее приверженцы находили, что универсалии существуют, но только в нашем уме; другие номиналисты, как мы увидим дальше, и это отрицали.

Концептуализм. Те номиналисты, которые признавали существование общих представлений, как психических явлений, называются концептуалистами (от conceptus mentis = понятия). Главный их представитель Локк (1632 — 1704). По его мнению, человек обладает способностью создавать общие представления и выражать эти общие представления при помощи слов. Человек может из ряда сходных представлений абстрагировать или выделить то общее, что в них содержится, отбросивши все случайное, что обусловливается теми или другими обстоятельствами. Посредством этого общего мы можем мыслить множество единичных предметов. Это отвлеченное или абстрактное общее и есть общее представление или понятие, которое существует у нас в уме. Следовательно, по Локку, объективно, реально существуют только единичные вещи, но мы о  единичных вещах имеем общее представление или понятие, которое, разумеется, существует только в нашем уме.

9

 

 

Номинализм. По мнению Беркли (1685—1763), таких абстрактных общих представлений, о которых говорит Локк, в нашем уме нет и быть не может. По его мнению, можно легко показать, что абстрактного общего представления о треугольнике не существует, потому что если бы таковое представление существовало, то оно должно было бы быть в одно и то же время представлением треугольника остроугольного и прямоугольного, равностороннего и равнобедренного, и в то же время ничем из них, потому что, строя общее представление треугольника, мы отвлекаемся от всех этих признаков. Точно так же общее представление или идея о человеке должна была бы быть в одно и то же время идеей о человеке черном, белом и смуглом, прямом и горбатом, большом, маленьком и среднего роста. Следовательно, по мнению Беркли, в нашем сознании нет абстрактных идей или общих представлений.

Но это утверждение вызывает недоумение: ведь общие представления существуют: иначе мы о них не были бы в состоянии говорить. Беркли согласен признать, что они существуют, но совершенно особенным образом. Если мы обратимся к нашему самосознанию, то в нашем уме мы не найдем общих представлений, в нашем уме есть только представления о единичных вещах, но они могут замещать собою общие представления. Для того, чтобы сделать эту мысль Беркли понятной, возьмем в пример геометра, который доказывает, каким образом можно разделить прямую линию на две части. Он проводит, например, чернилами черную линию длиной в один дюйм и на ней показывает, каким образом линия делится пополам. Эта линия есть единичная линия, но тем не менее она п о своему значению является общей, потому что в глазах геометра все то, что доказано относительно данной единичной линии, будет справедливо относительно всех других линий, или, другими словами, относительно линий вообще. Таким образом единичная линия становится общей, потому что она сделана знаком. Вследствие этого и слово «линия», которое есть частное слово, делается общим, благодаря тому, что становится знаком. Представление единичной математической фигуры приобретает общее значение, будучи на самом деле единичным.

10

 

 

Следовательно, по мнению Беркли, в нашем сознании находится представление единичных вещей, которое и играет роль заместителя, так что когда мы о чем-нибудь размышляем, то вместо понятий или общих представлений у нас появляются или единичные представления, или слова, которые замещают понятия, играя ту же роль, какую должны бы играть сами понятия, если бы они существовали.

Это—теория номиналистическая.

Таким образом у нас получаются две теории, именно теория концептуализма и теория номинализма. По номинализму, общих представлений или понятий нет, только слова придают тому или иному умственному построению общий характер. Но когда мы употребляем имена, слова, то в сознании мы имеем только представления о единичных вещах. По концептуализму, наоборот, наши представления могут быть общими; у нас могут быть представления класса вещей. Это — представления общих свойств ряда сходных единичных предметов.

Но какую из двух изложенных теорий нужно считать истинной? Первая теория более вероятна. В нашем уме нет понятий вроде каких-то схем: их замещают какие-нибудь единичные представления. (См. Психологию, гл. 21.)

Общие представления и понятия. Различие между общими представлениями и понятиями соответствует различию между понятиями просто и понятиями логически обработанными. Понятия просто—это те понятия, содержание которых мыслится неопределенным, в логически же обработанных понятиях мы всегда должны мыслить определенное содержание. Возьмем пример. Понятие «растение», «животное» в обиходной жизни употребляется с очень неопределенным содержанием. Вследствие этого простолюдин может быть в затруднении относительно того, есть ли, напр., морская анемона растение или же нет. Т. наз. морская анемона есть животное, по внешнему же виду она похожа на растение. Поэтому она в обиходной жизни и считается растением. Самое название «морские анемоны» или «морские розы» показывает, что популярное сознание не отличает их от растений. По тем же причинам простолюдин считает кита рыбой. Когда простолюдин употребляет слово «свет», то он думает о том общем, которое является результатом сравнения световых явлений,

11

 

 

которые он имел случай наблюдать: «пучок света», «солнечный луч», свет, который возникает в комнате после темноты, и т. п. Понятие света в физике, как научное понятие, употребляется со вполне определенным  содержанием. Физика предписывает нам, чтобы мы мыслили это понятие со вполне определенными признаками. Так как это понятие является со вполне определенным содержанием, то его следует считать логически обработанным понятием.

Таким образом различие между общими представлениями и понятиями сводится к большему совершенству этих последних. Их содержание более устойчиво, более определенно, более постоянно. В то время, как общие представления у различных лиц различны, понятия у всех людей должны быть одинаковыми.

Вопросы для повторения. Какой смысл имеет постановка вопроса о реальности понятий? Изложите взгляд Платона. Изложите взгляд Аристотеля на реальность понятий. Какое различие между учением Платона и Аристотеля? Какие существуют две теории об универсалиях? Что такое концептуализм? Что такое номинализм? Изложите теорию Беркли. Какое различие между концептуализмом и реализмом? Какое различие между общими представлениями и понятиями?

 

ГЛАВА 3-я.

О различных классах понятий.

Понятия и термины. Мы предполагаем начать с рассмотрения различных классов понятий. В сочинениях по логике у английских философов изложение логики обыкновенно начинается с рассмотрения терминов, имен или названий. Они исходят из того, что в логике мы должны трактовать не просто о понятиях, которые представляют известные умственные построения, но мы должны о них трактовать постольку, поскольку они получают выражение в языке, в речи; а так как понятия мы выражаем при помощи слов, названий и т. п., то, по их мнению, гораздо целесообразнее в логике говорить не о понятиях, а о названиях, именах или терминах.

Таким образом мы можем рассматривать или понятия в том виде, как они нами мыслятся, или их выражение при помощи слов.

12

 

 

Но на самом деле между этими двумя рассмотрениями нет существенной разницы. Как мы видели в Психологии, каждое понятие у нас в мышлении фиксируется, приобретает устойчивость, определенность, благодаря тому или другому слову, названию, термину. Когда мы в логике оперируем с понятием, то мы всегда имеем в виду понятие, которое связывается с известным словом. Слово является заместителем понятий. Мы можем оперировать только с теми понятиями, которые получили свое выражение в речи. Таким образом ясно, что все равно, будем ли мы говорить о названиях м терминах, как это делается в английской логике, или же будем говорить о понятиях просто.

V Понятия индивидуальные и общие. Понятия разделяются прежде всего на индивидуальные, или единичные, и общие. Индивидуальными понятиями мы будем называть те понятия, которые относятся к предметам единичным, индивидуальным (в данном случае индивидуальные понятия совпадают с представлениями о единичных вещах). Например, «британский посланник», «высочайшая гора в Америке», «автор Мертвых душ», «эта книга». К числу единичных понятий относятся также и собственные имена, например: «Софийский собор», «Ньютон», «Рим». Понятия, которые относятся к группе или классу предметов или явлений, имеющих известное сходство между собою, называются общими понятиями или классовыми понятиями. Например, понятия: «растение», «животное», «газ», «двигатель», «поступок», «движение», «красота», «гнев», «чувство» и т. п. суть понятия классовые или общие.

Общие, собирательные и разделительные термины. Единичные и общие понятия иногда могут употребляться в особенном смысле, и именно в так называемом собирательном. Если я произнесу предложение: «лес служит для сохранения влаги», то в этом предложении «лес» есть один из множества однородных предметов; в этом предложении понятие «лес» употреблено в общем смысле. Но «лес» может представляться как одно целое, состоящее из однородных единиц. В таком случае понятие «лес» или термин «лес» делается коллективным, или собирательным.

Собирательный термин обозначает одно целое, группу, состоящую из однородных единиц. Например, термины: «полк»,

13

 

 

«толпа», «библиотека», «лес», «парламент», «созвездие», «соцветие», «класс», представляют собою собирательные термины, если мы имеем ввиду, что они служат для обозначения целого, составленного из однородных единиц.

Но эти же самые термины делаются общими, когда мы их мыслим, как отдельные представители известного класса. Например, «полк», «толпа» есть общий термин, когда речь идет о «полках», о «толпах»; в этом случае вещи, обозначенные этими терминами, рассматриваются как известные единицы, входящие в состав известного класса сходных вещей. Если я употребляю термин «Румянцевская библиотека», «Английский парламент», то я употребляю термины собирательные, потому что они выражают известное целое, составленное из однородных единиц. Если же я скажу «европейские библиотеки, парламенты, университеты» и т. д., то это суть общие термины, потому что я говорю о библиотеках, парламентах, университетах как известном классе сходных предметов.

Как легко видеть из приведенных примеров, собирательные понятия представляют собою особую форму индивидуальных понятий.

Так как весьма часто общие понятия можно смешать с собирательными, то следует обратить внимание на следующее различие между ними. То, что мы утверждаем относительно понятия собирательного, относится к известному целому, составленному из единичных предметов, но это утверждение может быть неприложимо к предметам, входящим в это , целое и взятым в отдельности. Наоборот, то, что мы утверждаем относительно общего понятия, может быть приложено к каждому предмету, к которому относится это понятие. Собирательное понятие мыслится как одно целое, состоящее из однородных единиц; общее понятие мыслится как класс, который состоит из сходных предметов. Если мы говорим «парламент издал закон об отмене смертной казни», то мы этим хотим сказать, что известное целое, составленное из известных единиц, издало известный закон, но этого нельзя сказать относительно каждого члена парламента, потому что отдельные члены парламента могут высказаться за сохранение смертной казни. В этом случае понятие «парламент» употреблено в собирательном

14

 

 

смысле. Но я могу употребить выражение «парламенту принадлежит законодательная функция»; в этом случае термин «парламент» употреблен в общем смысле, потому что указанное выражение справедливо относительно всех парламентов.

Иногда мы можем употреблять те или иные понятия таким образом, что наши утверждения будут справедливы относительно каждой отдельной единицы, входящей в ту или другую группу предметов. Такое употребление терминов или понятий мы будем называть употреблением в разделительном смысле. Когда мы употребляем какое-нибудь понятие в собирательном смысле, то мы наше утверждение относим к группе, рассматриваемой в целом; если же мы употребляем его в смысле разделительном, то мы утверждаем что-либо о каждом члене группы раздельно. Если мы, например, говорим: «весь флот погиб во время бури», то мы употребляем понятие «весь» в собирательном смысле, потому что мы говорим о флоте, взятом в целом. Отдельные корабли могут не погибнуть, но флот, как известное целое, перестает существовать. Если мы употребляем выражение «все рабочие утомились», то в нем слово «все» мы употребляем в разделительном смысле, потому что мы имеем в виду утомление каждого рабочего в отдельности.

Абстрактные и конкретные термины. Абстрактные термины это такие термины, которые служат для обозначения качеств или свойств, состояний, действия вещей. Они обозначают качества, которые рассматриваются сами по себе, без вещей. Когда мы употребляем абстрактные термины, то мы совсем не имеем в виду обозначить, что соответствующие этим терминам качества или свойства, состояния вещей существуют где-нибудь в определенном пространстве или в определенный момент времени, а, наоборот, они мыслятся нами б е з  вещей, а потому и без определенного пространства и времени. Примером абстрактныхтерминов могут служить такие термины, как: «тяжесть», «объем», «форма», «цвет», «интенсивность», «твердость», «приятность», «вес», «гуманность». В самом деле, «тяжесть» не есть что-нибудь такое, что имеет существование в данный момент времени: она существует не только

15

 

 

в каком-нибудь определенном месте, но и везде, где только есть тяжелая вещь. Абстрактные термины называются так потому, что свойства или качества, обозначаемые ими, могут мыслиться без тех вещей, к которым они принадлежат: мы можем абстрагироваться, отвлекаться (abstra­here) от представления тех или иных вещей.

Абстрактными, в отличном от этого смысле, иногда называются также и понятия таких вещей, которые не являются предметом чувственного восприятия, т.е. не могут восприниматься нами, как известная определенная вещь, например, «вселенная», «звездная система», «тысячеугольник», «человечество» и т. п. Но в этом случае было бы целесообразнее такие понятия называть понятиями, лишенными наглядности (по-нем. unanschaulich), в противоположность тем понятиям, которые могут являться предметом чувственного восприятия и которые поэтому могут быть названы наглядными или интуитивными.

Конкретными являются понятия вещей, предметов, лиц, фактов, событий, состояний сознания, если мы рассматриваем их имеющими определенное существование, например: «квадрат», «пламя», «дом», «сражение», «страх» *) и т. п. Отношение между абстрактными понятиями и конкретными следующее. Абстрактное понятие получается из конкретного; мы путем анализа выделяем какое-нибудь качество или свойство вещи, например, «белизну» из «мела». С другой стороны, на конкретное понятие можно смотреть как на синтез абстрактно мыслимых качеств. Например, понятие «камень» представляет собою синтез качеств: «тяжесть», «шероховатость», «твердость» и т. п.

Надо заметить, что прилагательные всегда являются терминами конкретными, а не абстрактными; употребляя прилагательное «белый», мы всегда мыслим вещь, свойство же или качество мы мыслим в том случае, когда мы употребляем существительное «белизна».

В языке иногда абстрактные и конкретные термины упо-

*) О чувстве страха можно сказать, что оно имеет известное качество напр. известную силу или интенсивность, что оно обладает свойством парализовать умственную деятельность и т. д. Словом, оно может быть рассматриваемо как нечто, состоящее из совокупности свойств или качеств.

16

 

 

требляются попарно. Например, конкретному термину «белый» соответствует абстрактное понятие «белизна»; конкретному термину «строгий» соответствует абстрактный «строгость»; квадрат—квадратность, человек—человечность.

Термины положительные и отрицательные. Положительные термины характеризуются тем, что они служат для обозначения наличности того или другого качества. Например, употребляя термины «красивый», «делимый», «конечный», мы желаем обозначить, что в предметах имеются налицо качества, означаемые этими словами, соответствующие же им отрицательные термины «некрасивый», неделимый», «бесконечный» будут означать, что указанные качества отсутствуют, не имеются налицо. Другие примеры отрицательных терминов: «вневременный», «сверхчувственный», «ненормальный», «беспечный», «бессмысленный».

Относительные и абсолютные термины. Есть, наконец, термины относительные и абсолютные. Что значит вообще абсолютный? Под абсолютным мы понимаем то, что не находится в связи с чем-либо другим, что не зависит от  чего-либо другого; под относительным мы понимаем то, что приводится в связь с чем-нибудь другим. Абсолютный термин—это такой, который в своем значении не содержит никакого отношения к чему-либо другому, он не принуждает нас мыслить о каких-либо других вещах, кроме тех, которые он обозначает. Например, термин «дом» есть термин абсолютный. Мысля о доме, мы можем не думать ни о чем другом. Относительный же термин—это такой термин, который, сверх того предмета, который он означает, предполагает существование также и другого предмета. Например, термин «родители» необходимо предполагает существование «детей»: нельзя мыслить о родителях без того, чтобы в то же время не мыслить о детях. Если мы говорим о каком-либо человеке, что он «строгий», то мы наше внимание можем ограничить только этим человеком; но если мы говорим о нем, как о «друге», то мы должны подумать еще об одном лице, которое стоит к нему в отношении дружбы. Другие примеры: «компаньон», «партнер», «сходный», «равный», «близкий», «король—подданные», «причина—действие», «северный— южный». Каждый из такой пары терминов называется соотносительным другому термину.

17

 

 

Вопросы для повторения. Какое существует соотношение между рассмотрением терминов и понятий? Какие термины общие и какие индивидуальные? О каких терминах мы говорим, что они употреблены в собирательном смысле и о каких—в разделительном смысле? Какое различие между собирательными терминами и общими? Какие термины называются абстрактными и какие конкретными? Какие термины называются положительными, отрицательными? Какие термины относительные и абсолютные?

 

Г Л A В А 4-я.

Содержание и объем понятий.

Признаки понятий. Понятия, как мы видели в Психологии, получаются из сравнений сходных представлений. Представления, в свою очередь, складываются из отдельных элементов. Составные элементы представления или понятия принято называть признаками. Признаки есть то, чем одно представление или понятие отличается от другого. Напр., признаками золота мы считаем «металл», «драгоценный», «имеющий определенный удельный вес» и т. п. Это все то, чем золото отличается от других вещей, от не-металлов, от недрагоценных металлов и т. п.

Не все признаки нужно считать равноценными. Каждое понятие имеет множество различных прйзнаков, но при мышлении о нем мы прежде всего по преимуществу мыслим только известные признаки. Эти признаки являются как бы основными, около которых группируются другие признаки. Первые признаки называются существенными или основными, а остальные—второстепенными. Основные признаки—это такие признаки, без которых мы не можем мыслить известного понятия и которые излагают природу предмета. Например, для ромба существенным является тот признак, что он есть четырехугольник с параллельными и равными сторонами и т. п.; несущественным для понятия ромба является тот признак, что он имеет ту или другую величину сторон, ту или другую величину углов.

Признаки понятий со времени Аристотеля принято делить на следующие 5 классов:

1) Родовой Признак. Если мы скажем, что «химия» есть «наука», то «наука» будет родовым признаком для понятия «химия»; в числе других признаков, присущих понятию

18

 

 

«химия», есть и признак «наука»; этот признак отличаем химию от всего, что не есть паука. Род (genus) или родовой признак есть понятие класса, в который мы вводим другое рассматриваемое нами понятие.

2) Видовое различие. Если мы скажем, что «химия» есть паука, «занимающаяся изучением строения вещества», то прибавление признака—«занимающаяся изучением строения вещества»—будет служить для обозначения того, чем эта наука отличается от других «наук». Такой признак, который служит для того, чтобы выделять понятие из ряда ему подобных понятий, называется видовым различием (differentia specifica). Возьмем понятия: «моряк русский», «моряк французский», «моряк немецкий». В этом случае «русский», «французский», «немецкий» есть видовое различие; оио служит для того, чтобы выделить моряка одной нации от моряков всех прочих наций.

3) Вид (species). Если к родовому признаку придать видовое различие, то получится вид. Например, «здание для склада оружия»=арсенал; «здание для склада хлеба»= амбар. В этом случае «здание» есть род, «для хранения оружия» есть видовое различие; присоединение к роду видового различия дает вид «арсенал». Присоединение к понятию «здание» видового признака «служащее для хранения хлеба» дает вид «амбар». Вид может быть признаком, потому что его можно приписать понятию. Напр., эта наука есть химия.

Собственный признак (Proprium). Собственный признак—это такой признак, который присущ всем вещам данного класса. Кроме того, это такой признак, который не содержится в числе существенных признаков, но который может быть выведен из них. Напр., существенным признаком человека является его «разумность». Из этого свойства вытекает его способность «владеть речью». Этот последний признак есть собственный признак. Основной признак треугольника—это прямолинейная плоская фигура с тремя сторонами. Что же касается того признака треугольника, что сумма углов его равняется двум прямым, то это есть его собственный признак, потому что вытекает или выводится из основных признаков. Мы этого признака не мыслим, когда думаем о треугольнике; поэтому он является выводным.

19

 

 

5) Несобственный признак (Accidens). Несобственный признак—это такой признак, который не может быть выведен из существенного признака, хотя и может быть присущ всем вещам данного класса. Напр., черный цвет ворона есть accidens. Если бы черный цвет ворона был выводим из основных свойств его, то он мог бы быть назван proprium, но он не выводим, так как мы не знаем, по какой причине вороны имеют черный цвет перьев. Он есть, следовательно, accidens.

Несобственные признаки делятся на две группы: на неотделимые несобственные признаки (accidens inse­parabile) и отделимые несобственные признаки (accidens separabile). Последние суть те признаки, которые присущи только некоторым вещам того или другого класса, по не всем, а первые присущи всем  вещам данного класса. Напр., черный цвет ворона есть accidens inse­parabile. Черный цвет волос для человека есть accidens separabile, потому что есть люди, которые не имеют черного цвета волос. По отношению к отдельным индивидуумам несобственный признак также может быть отделимым и неотделимым. Отделимые это такие признаки, которые в одно время имеются налицо, а в другое время не имеются. Напр.: Бальфур—первый министр Англии. Через некоторое время он может не быть первым министром. Это есть признак отделимый. «Лев Толстой родился в Ясной Поляне». В этом предложении признак «родился в Ясной Поляне» есть неотделимый признак.

Содержание и объем понятия. Понятия могут быть рассматриваемы с точки зрения содержания и объема.

Содержание понятия—это то, что мыслится в понятии. Напр., в понятии «сахар» мыслятся признаки: сладкий, белый, шероховатый, имеющий тяжесть и т. д.; эти признаки в совокупности и составляют содержание понятия сахар. Содержание понятия, другими словами, есть сумма признаков его; поэтому каждое понятие можно разложить на ряд присущих ему признаков. Содержание понятия может быть весьма изменчивым в зависимости от принятой точки зрения, от размера знания и т. п. Напр., в понятии сахар химик мыслит одно содержание, а простолюдин другое.

20

 

 

Объем понятия есть то, что мыслится посредством понятия, т.-е. объем понятия есть сумма тех классов, групп, родов, видов и т. п., к которым данное понятие может быть приложено. Напр., объем понятия животное: птица, рыба, насекомое, человек и т. д.; объем понятия элемент: кислород, водород, углерод, азот и т. д. Объем понятия четырехугольник: квадрат, прямоугольник, ромб, трапеция.

Таким образом различие между объемом понятия и содержанием понятия сводится к следующему. Объем означает ту совокупность предметов, к которым должно прилагаться данное понятие, а содержание обозначает те признаки, которые приписываются тому или другому понятию.

Для более ясного представления объема понятий и отношения объемов существует особый прием, называемый «логическою символикою».

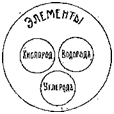
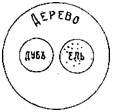На рис. 1-м большой круг символизует собою понятие «элемент», а меньшие круги, в нем находящиеся, символизуют понятия, входящие в его объем. Если мы изображаем какой-нибудь круг внутри другого круга, то мы этим символизуем, что объем одного понятия входит в объем другого. Из рис. 2-го видно, что понятие «дерево» содержит в своем объеме понятия:«дуб», «ель» и т. II. Отдельные точки в круге «ель» символизуют индивидуальные или единичные ели.

Понятие с большим объемом называется родом по отношению к тому понятию с меньшим объемом, которое входит в его объем. Понятие с меньшим объемом в этом случае называется видом. Понятия с большим объемом можно назвать также понятиями более широкими или более общими.

Любой вид может сделаться родом. Например, понятие «пальма» относится к понятию «дерево», как вид к роду; но в свою очередь оно относится уже как род к своим видам—«пальма кокосовая», «пальма фиговая» и т. д. Вообще более общее понятие есть род для менее общего понятия;

21

 

 

 более общее понятие представляет собою родовое понятие для менее общего, менее общее само становится родом для еще менее общего и т. д., пока мы не придем к такому понятию, которое уже не может в своем объеме содержать какие-либо другие виды, а может подразделяться только на отдельные индивидуумы.

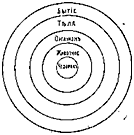
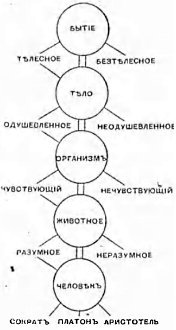Следует упомянуть о попытке греческого философа Порфирия (233—304) при помощи схемы облегчить понимание отношения между обнимающими друг друга понятиями, т.-е. понятиями, из которых одно входит в объем другого. Эта схема называется «деревом Порфирия». В понятие «бытия» (т.-е. того, что вообще существует) входит понятие «телесного бытия» и «бестелесного бытия». «Тело» содержит в своем объеме «одушевленное тело» или «организм» и «неодушевленное тело». Понятие организм содержит в своем объеме «чувствующие» и «нечувствующие организмы» (т.-е. растения). «Чувствующие организмы» содержат в своем объеме разумные и неразумные существа и х. д.

«Бытие» есть высший род, который уже не может быть видом для другого рода. Такой род называется summum genus; «человек»—это есть низший вид. В его объем уже не входят понятия с меньшим объемом, а входят только отдельные индивидуумы. Такое понятие называется infima species (самый низший вид). Ближайший высший класс или род того или другого вида называется proximum genus (ближайший род). Отношение между более широкими и узкими понятиями можно изобразить и иначе, именно поместивши круги, служащие для обозначения понятий с меньшим объемом, внутри кругов, служащих для обозначения понятий с большим объемом. (См. рис. За.)

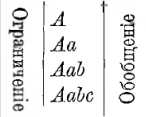
Ограничение и обобщение. Процесс образования менее общих понятий из более общих называется ограничением

22

 

 

(determinatio). Для образования менее общего понятия мы должны к более общему прибавить несколыю признаков, благодаря чему понятие уясняется (determinatur). Например, чтобы из понятия «дерево» получить менее общее понятие «пальма», иадо к признакам «дерева» прибавить специальные признаиш «пальмы»: вид ее листьев, прямизну ствола и т. д. Обрахный процесс образования более общего понятия из менее общего, при котором, наоборот, иекоторое количество признаков от данного понятия отнимается, называется обобщением (generalisatio).

Род образуется из видов при помощи процесса обобщения, и наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы.

Предположим, что у нас есть понятие А (наука). Из него при помощи видового различия а мы можем образовать вид Aа (математика); прибавивши к понятию Aа видовое различие  (определение пространственных отношений), получим геометрию Аа. Прибавив к этому виду признак с (определение пространственных отношений на плоскости), получим планиметрию.

Обратный процесс—получение более общих понятий путем отбрасывания отдельных признаков—будет называться обобщением. И тот и другой процесс можно изобразить при помощи след. схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наоборот, восхождение от менее общих к более общим понятиям.

Отношение между объемом и содержанием понятия. Для того чтобы ответить на вопрос, какое существует отношение между объемом и содержанием понятия, возьмем какой-нибудь пример. Объем понятия «человек» обширнее, чем,

23

 

 

например, объем понятия «негр». Употребляя понятие «человек», мы думаем обо всех людях, мы думаем о людях, живущих во всех пяти частях света, между прочим и в Африке; употребляя понятие «негр», мы думаем только о тех людях, которые живут в Африке. Но о содержании этих двух понятий следует сказать как раз наоборот: содержание понятия негр будет обширнее понятия человек. Когда мы говорим о негре, то мы можем найти в нем все признаки понятия «человек» плюс еще некоторые особенные признаки, как-то: черный цвет кожи, курчавые волосы, приплюснутый нос, толстые губы и т. п.

Итак, по мере увеличения содержания понятия уменьшается его объем и наоборот.

Вопросы для повторения. Что такое признаки понятий? Какие признаки понятий мы отличаем? Что такое родовой признак? Что такое видовое различие? Что такое вид? Что такое собственный признак? Что такое несобственный признак? Что такое содержание понятия? Что такое объем понятия? Что такое summum genas? Что такое infima species? Что такое обобщение? Что такое ограничение? Какое существует отношение между объемом и содержанием понятия?

 

 

ГЛАВА 5-я.

Логические категории и отношения между понятиями.

Категории. Ни один предмет не представляет собою чего-либо совершенно отличного от всех других предметов, но он похож на них в каком-либо отношении: его всегда можно отнести в какой-либо общий класс с другими предметами; все вообще предметы могут быть относимы в общие с другими предметами классы. Есть классы, которые обнимают небольшое количество предметов, но есть классы, которые обнимают небольшое количество предметов, и именно потому, что это суть предметы с самыми общими сходствами. Эти классы вещей в нашем мышлении получают выражение в виде известных понятий. Такие понятия, которые служат для обозначения самых общих сходств между предметами, Аристотель назвал категориями. Слово «категория» происходит от греческого слова κατηγορέω, что значит «высказывать»,

24

 

 

«быть сказуемым». Категории для Аристотеля суть возможные предикаты какого-либо единичного предмета, т.-е. такие понятия, которые можно высказать относительно того или иного единичного предмета или класса предметов. Вот эти категории:

1) Субстанция (substantia).

2) Количество (quantitas).

3) Качество (qualitas).

4) Отношение (relatio).

5) Место (ubi).

6) Время (quando).

7) Положение (situs).

8) Обладание (habitus).

9) Действие (actio).

10) Страдание (passio).

Под эти десять категорий, по мнению Аристотеля, подходит все то, что можно мыслить. Если мы желаем высказать о  тех или других вещах что-либо самое общее, то мы не можем о них высказать ничего другого, кроме того, что они суть или субстанции, или что они обозначают качество, отношение, местои т.п. Других точек зрения, кроме тех, которые содержатся в категориях, не существует. Таким образом можно сказать, что категории представляют собою наиболее общие классы всего мыслимого.

В новейшей философии в качестве наиболее общих классов мыслимого философы различают вещь, свойство, отношение. Все, о чем мы можем мыслить, есть или вещь (субстанция), или это есть свойство (атрибут), или, наконец, это есть отношение.

Под вещами мы понимаем то, что обладает большим или меньшим постоянством формы. Например, таким постоянством обладают камень, дерево, жидкость в сосуде и т. п. Кусок камня сегодня обладает той же формой, какой он обладал вчера: нам представляется, что такое постоянство будет ему присуще и впоследствии.

Вещи мы представляем имеющими известные свойства или качества, или мы представляем их совершающими известные действия, или находящимися в известном состоянии. Например, то, что кусок железа имеет известную тяжесть, есть его свойство или качество. Если кусок

25

 

 

железа накален, то это ость его состояние; если кусок железа плавится или движется, то это есть известный процесс, деятельность. Свойства, действия, состояния мы представляем принадлежащими известной вещи, как известной носительнице их. Но в то же время мы их мыслим, как элементы, из которых состоит вещь: мы мыслим железо, как нечто имеющее известную тяжесть, твердость, способность накаляться, приходить в движение и т. и. Качество, действие, состояние, мы будем называть одним общим именем — свойства вещи.

Одна вещь может мыслиться нами находящейся в различных отношениях к другой вещи. Одна вещь может быть больше, чем другая (пространственное отношение); одна вещь может быть причиной другой вещи (причинное отношение); одна вещь может возникнуть раньше, чем другая (временное отношение), и т. п.

Все, что мы можем мыслить, мы должны мыслить под одной из этих категорий, т.-е. все, что мы мыслим, мы должны мыслить или как вещь, или как свойство вещи, или как отношение. Эти три наиболее общих понятия мы и считаем категориями.

Этим исчерпывается вопрос о категориях.

Отношений между понятиями. Рассмотрим логические отношения, существующие между понятиями.

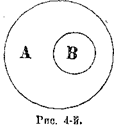1. Подчинение понятий (subordinatio notionum) мы имеем в том случае, когда одно понятие относится к другому, как вид к своему роду, когда одно понятие входит в объем другого, как часть его объема. Для примера возьмем понятие «дерева» А и понятие «березы» В. Это последнее понятие входит в объем первого. (Символ подчинения понятий см. на рисунке 4-м.) Другие примеры: «душевная деятельность» и «ощущение вкуса»; «человек», «математик».

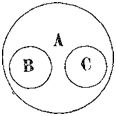
2. Соподчинение понятий (coordinatio notionum) мы имеем в том случае, если в объем одного и того же более широкого понятия входят два или несколько одинаково подчиненных ем низших понятия. Эти низшие понятия называются соподчиненными (координированными). Наприм., «мужество» В,

26

 

 

«умеренность» С, «добродетель» А. Оба первых, понятия входят в объем последнего (см. рис. 5-й).

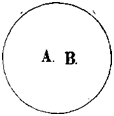
3. Понятия равнозначащие (notiones aequipollentes). Для разъяснения этого отношения возьмем два понятия: «английский народ» и «первые мореплаватели в мире». Когда мы произносим слова «английский народ» и при этом имеем в уме понятие «английский народ», мы думаем об англичанах. Когда мы произносим слова «первые мореплаватели», то мы также думаем об англичанах; следовательно, объем этих двух понятий один и тот же. Раскроем теперь содержание этих понятий. В понятии «английский народ» мы мыслим известное политическое устройство, известную территорию, известную культуру и т. д., в понятии же «первые мореплаватели»— известное искусство в постройке кораблей и управлении ими, известное развитие морской торговли, многочисленность флота и т. д.; следовательно, содержание этих понятий различно. Если у нас есть два понятия с различными содержаниями, но одинаковые объемом, то такие понятия называются равнозначащими. (Другие примеры: «христианин—крещеный», «органический—смертный», «величайший современный писатель» — «автор Войны и мира». Равнозначащие понятия можно символизовать при помощи двух кругов, сливающихся в один, подобно тому как сливаются объемы указанных понятий; различие же содержания символизуется двумя различными буквами, стоящими в этом круге (см. рис. 6-й).

4. Противные и противоречащие понятия. На эти два различных класса понятия, очень сходных по своим внешним свойствам, но в то же время совершенно различных по существу, следует обратить особенное внимание и хорошенько продумать их различие, так как при оперировании с ними легко впасть в ошибку.

Если мы возьмем объем какого-нибудь понятия и будем распределять по степени сходства виды, входящие в него, таким образом, что после каждого вида мы будем

27

 

 

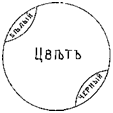брать следующий наименее от него отличный, то в конце концов из этих понятий-видовполучится ряд,в котором первый и последний член очень сильно отличаются друг от друга. Эти-то два понятия, первое и последнее во взятом нами ряде видов, находятся в отношении противности или противоположности. Будем, напр., указанным способом распределять виды понятия «цвет». В его объем входят различные оттенки всевозможных цветов: в его объеме мы можем найти цвета: красный, зеленый, черный, белый, серый и т. п. Если мы указанным выше способом будем размещать виды в ряд по мере сходства их, то мы можем получить приблизительно следующий ряд: белый, беловатый..., светло-серый..., серый..., темно-серый,.., черноватый..., черный. Как видно из этого, наибольшее различие здесь между понятиями «белый» и «черный»; они-то и суть противоположные или противные понятия. Итак, понятия, входящие в один и тот же объем, но очень отличающиеся друг от друга, называются противными (contrariae). Схема: в круге, символизующем объем какого-нибудь понятия, двумя линиями, отделены два крайних отрезка, один против другого (см. рис. 7-й). Другие примеры: добрый, злой; высокий, низкий; красивый, уродливый; громкий, тихий; глубокий, мелкий. Надо заметить, что не все понятия имеют противные им понятия. Напр., понятие «голубой» не имеет противного ему понятия.

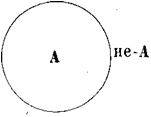Если мы имеем какое-нибудь понятие А и другое понятие В, относительно которого известно только то, что оно не есть А, то такие понятия называются противоречащими (contradictoriae). Например, понятия «белый» и «не-белый» суть понятия противоречащие. Итак, два термина, из которых один получен путем прибавления отрицательной частицы «не» к другому, относятся между собой, как противоречащие. Символически отношение между противоречащими понятиями выражается следующим образом (см. рис. 8-й). Кру-

28

 

 

гом символизуется какое-нибудь одно понятие «А» и вне его ставится другое понятие «В», которое есть «не-А», при чем это понятие В может быть поставлено где угодно, лишь бы не внутри круга, не в его объеме; это второе понятие по своим свойствам называется понятием отрицательным или неопределенным (notio negativa seu indefinita) *).

Если мы возьмем для сравнения два понятия противоречащие и противоположные,

белый—черный.

белый—не-белый.

то мы можем наглядно убедиться, что разница между этими двумя логическими отношениями огромная: тогда как второй член первой пары (черный) имеет вполне определенное содержание, которое можно представить, второй член второй пары (не белый) такого определенного содержания не имеет: его содержание отличается неопределенностью, т. е., употребляя слово «не-белый»_; мы можем под ним понимать и красный, и зеленый, и синий, и даже большой, красивый, добрый и т. п.

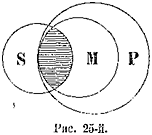
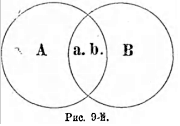5. Скрещивающиесяпонятия (notiones inter se convenientes). Если мы имеем два понятия, содержание которых различно, по объемы некоторыми своими частями совпадают, то таких два понятия называются скрещивающимися. Возьмем два понятия, напр.: А—негры и В—рабы. В объеме понятия «негры» заключается часть объема понятия «рабы», ибо некоторые негры суть рабы; и с другой стороны, в объеме понятия «рабы» заключается некоторая часть объема понятия «негры», ибо некоторые из рабов суть негры. Это мы могли бы изобразить при помощи схемы на рис. 9.

Так как та часть объема понятия «негры», которая состоит из рабов, и та часть объема понятия «рабы», которая состоит из негров, логически между собою равны, то

*) Сюда же относятся понятия, которые вообще получены отрицательным путем, напр., бесконечный, бесспорный и т. п., если эти понятия могут быть символизованы только что указанным способом.

29

 

 

символически их можно представить равными частями двух кругов, которые при наложении могли бы совпасть. Поэтому схемой скрещивающихся понятий могут служить два скрещивающихся круга, причем круги символизуют объемы данных понятий, а место их совпадения совпадающие, логически равные части этих объемов. Другой пример: «прямоугольные фигуры» и «параллелограммы», ибо некоторые прямоугольные фигуры суть параллелограммы, и некоторые параллелограммы суть прямоугольные фигуры.

6. Понятия несравнимые (notiones disparatae). Возьмем два понятия: «душа» и «треугольник». Для этих двух понятий нет общего ближайшего родового понятия, в объем которого они могли бы оба войти, как координированные. Между ними нет ничего такого общего, что могло бы для них явиться посредствующим, связывающим элементом, на основании которого их можно было бы сравнить. Такие два понятия находятся в логическом отношении несравнимости. Для того, чтобы можно было сравнить два понятия, необходимо нечто третье, что объединяло бы эти понятия—это именно ближайшее общее понятие, в объем которого они входили бы. Это третье понятие называется tertium compara­tionis.

Следует заметить, что речь идет об отсутствии ближайшего родового понятия. Если мы возьмем, напр., два таких понятия, как «корабль» и «чернильница», то при всем различия их они имеют нечто общее (и то, и другое есть вещь), но нет ближайшего родового понятия, в объем которого они входили бы.

Вопросы для повторения. Что такое категория? Какие категории признавал Аристотель? Какие следует признавать категории? Что такое вещь, свойство, отношение? Что такое подчинение понятий? Приведите примеры. Что такое соподчинение понятий? Приведите примеры. Какие понятия называются равнозначащими? Приведите примеры. Какие понятия называются противными или противоположными? Приведите примеры. Какие понятия называются противоречащими? Приведите примеры. Что такое скрещивающиеся понятия? Приведите примеры. Какие понятия несравнимые? Что необходимо для того, чтобы понятия можно было сравнивать?

30

 

 

ГЛАВА 6-я.

Об определении.

Цель определения. Когда мы произносим какое-либо слово, соответствующее известному понятию, и хотим сделать его понятным для всех, то мы должны раскрыть содержание понятия, соответствующего указанному слову, а так как содержанием понятия называется совокупность его признаков, то «раскрытие» содержания понятия можно обозначить как перечисление признаков, присущих данному понятию. Какое-либо понятие А содержит признаки а,  b, с, d; если мы перечислим эти признаки, то тем самым точно обозначим, раскроем содержание понятия А; это значит, другими словами, что мы определим его.

Следует заметить, что не все понятия могут быть определены.

Понятия по своему содержанию бывают весьма различны: содержание одних понятий больше, других меньше. Такие понятия, которые имеют сложное содержание, т.-е. такие, которые имеют много признаков, могут быть определены. Но есть понятия, которые имеют настолько простое содержание, что не могут быть определены, потому что, как было сказано, для определения необходимо раскрытие содержания понятия; если же содержание понятия не может быть раскрыто, то оно не может быть и определено. Такие понятия называются простыми. Например, понятие «пунцового цвета» не подлежит определению: цвет этот нужно видеть, чтобы знать, что он такое. Все же определения, которые мы попытались бы дать в данном случае, были бы ложными в логическом отношении. Точно так же определять, что такое тон известной высоты, бесполезно; это усваивается, понимается непосредственным восприятием этого тона. Сюда же относятся такие понятия, как, например, понятия «равенства», «тождества», «тяжести», «протяжения» «сознания» и т.п. Точно так же не могут быть определяемы индивидуальные понятия, потому что при определении их пришлось бы перечислить бесконечное множество признаков. Напр., «этот бриллиант».

31

 

 

Итак, определить то пли иное понятие значит перечислить его признаки. Но это представляется иногда задачей трудной, потому что количество признаков того или другого понятия может быть очень велико, поэтому перечислить даже большинство этих признаков не окажется возможным. Если бы, например, определяя понятие «прямоугольника», мы сказали, что прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырехугольная с прямыми углами и т. д., то это определение было бы правильно, но практически оно неудобно потому, что перечисляется целый ряд признаков. Вследствие этого принят другой способ определения понятий, который имеет целью избежать полного перечисления признаков. Он заключается в следующем.

Дадим определение прямоугольника. Для этой цели мы воспользуемся понятием параллелограмма. Когда мы употребляем термин параллелограмм, то мы под ним понимаем прямоугольник, ромб, квадрат. Зная это, мы не будем говорить: «прямоугольник есть геометрическая фигура, плоская, ограниченная прямыми линиями, четырехугольная» и т. д., а просто скажем, что это есть «параллелограмм, в котором все углы прямые», ибо, произнося слово параллелограмм, мы предполагаем, что всякий разумеет под ним геометрическую фигуру, ограниченную четырьмя прямыми, попарно параллельными линиями; прибавляя, что все углы ее прямые, мы окончательно завершаем определение ее, именно тем, что мы отличаем прямоугольник от ромба и от квадрата, которые тоже суть параллелограммы. Таким образом, определяя понятие прямоугольника, мы указали род данного понятия (параллелограмм) и присоединили к нему видовое различие его (четыре прямых угла), отличающие его от других видов, входящих в тот же род, т.-е. от ромба и квадрата. Руководствуясь тем же правилом, мы скажем, что ромб есть параллелограмм, в котором все стороны «равны», «квадрат есть параллелограмм, в котором стороны и углы равны».

Итак, определение заключается в указании рода данного понятия с присоединением видового различия его. Это в логике принято обозначать при помощи формулы: Defiinitio

32

 

 

fit per genus et differentiam specificam», т.-е. определение совершается при помощи рода и видового различия *).

Если нам нужно определить какое-либо понятие, то мы выражаем наше определение при помощи суждения, содержащего подлежащее и сказуемое. Подлежащее этого суждения называется определяемым (definiendum), сказуемое называется определяющим (definiens). Эти термины важны потому, что, благодаря им, мы можем указать те правила, при соблюдении которых получается правильное определение. Таких правил четыре.

1) Определение должно быть соразмерным, т.-е. таким, в котором объемы определяемого и определяющего тождественны, т.-е. одинаково велики. Если правило это нарушено, то определение неадекватно, или несоразмерно. В таком случае определение делается или слишком широким, или слишком узким, именно, если объем определяющего становится слишком широким или слишком узким в сравнении с объемом определяемого. Возьмем в пример определение лошади. Если сказать, что «лошадь есть домашнее животное», то это определение будет слишком широким; в нем объем определяющего будет более широким, чем объем определяемого понятия (в объем домашнего животного, кроме лошади, входят еще коровы, собаки и т. п.). Относительно такого определения можно также сказать, что в него не входит указание существенного признака данного понятия. Если в определении опущены существенные признаки понятия, тогда оно окажется слишком широким, как в только что приведенном примере.

Возьмем определение, которое погрешает в противоположном направлении. Если бы мы сказали, что «треугольник есть плоская прямолинейная фигура, имеющая три равных стороны, то это определение было бы слишком узким. В нем объем определяющего понятия меньше объема определяемого понятия. Именно, между тем как в объем определяющего понятия входят только равносторонние треугольники, в объем определяемого входят как равносторонние, так и неравносторонние.

*) Другие в этой формуле прибавляют к genus термин proximum, „Definitio fit per genus proximum et differentiam specificam“, желая этим указать на то, что следует пользоваться ближайшим родовым понятием.

33

 

 

2) Определение не должно делать круга. Это правило требует, чтобы определяемое понятие не-определялось посредством понятия, которое само делается понятным, только посредством определяемого. Возьмем, например, определение: «вращение есть движение вокруг оси». Это определение понятия «вращения» посредством понятия «оси» делает круг, ибо само понятие оси определяется только через понятие вращения (как известно, ось—это прямая, вокруг которой происходит вращение). Таким образом ясно, что в нашем определении получается круг: понятие «вращения» определяется посредством понятия оси», а понятие «оси»—посредством понятия «вращения».

В определении определяющее и определяемое должны быть двумя различными и притом самостоятельными понятиями. Если это не соблюдается, то получается ошибка, которая называется idemperidem, или тавтологией, именно, в определении получается только повторение того же слова, т.-е. употребляются слова, имеющие то же самое значение. Например, «свет есть то, чему присущ свет»; «величина есть то, что способно уменьшаться и увеличиваться». Последнее определение представляет собою тавтологию потому, что уменьшение есть убавление величины, увеличение же есть прибавление величины, а потому, если мы определяем величину посредством того, что способно увеличиваться или уменьшаться, то очевидно, что в определяющем понятии содержится определяемое понятие.

3) Определение не должно быть отрицательным, оно должно указывать признаки, присущие данному понятию, а не чуждые ему, ибо эти последние для нас неважны и, кроме того, их можно указать очень много. Например, возьмем определение: «театр есть здание, не служащее для жилья». Если А будет здание служащее для жилья, то не-А,. или зданий, не служащих для жилья, будет бесчисленное множество. Таким образом это определение делается для нас непригодным. К числу таких определений, которые вследствие отрицательного характера непригодны, нужно отнести: «жидкость есть то, что не твердо и не газообразно», «точка есть то, что не имеет частей и не имеет никакой величины». Отрицательные определения не раскрывают содер-

34

 

 

жания понятия, они оставляют содержание понятия неопределенным. Поэтому отрицательные определения не отвечают главной цели определения—раскрыть содержание определяемого понятия, сделать содержание понятия определенным.

Отрицательные определения могут быть употребляемы только тогда, когда определяемое понятие имеет отрицательный характер. Напр., «чужестранец»—это человек, не принадлежащий к данной стране.

4) Определение должно быть ясным, т.-е. в определении нельзя пользоваться выражениями двусмысленными, метафорическими и вообще мало понятными. Нарушение этого правила приводит к попытке сделать понятным неизвестное через посредство еще менее известного (ignotum per ignotius). Например, если сказать, что «архитектура есть застывшая музыка», «нужда есть мать изобретения», то это суть образные выражения, которые не объясняют значения термина. Если же сказать, что «эксцентричность есть своеобразная идиосинкразия», то мы непонятное пытаемся объяснить посредством непонятного же.

Приемы, заменяющие определения. Итак, чтобы наши определения были точны, они должны удовлетворять указанным четырем условиям. Но не следует думать, что все наши понятия могут быть всегда определяемы указанным способом. Есть случаи, когда нам приходится знакомиться е содержанием понятия не через посредство определения, а иными способами. Можно указать следующие способы, заменяющие определение.

1) Указание. Если, например, мы кого-нибудь желаем познакомить с тем, что такое тот или другой цвет, звук и х. п., то это мы будем в состоянии сделать только в том случае, если приведем его в соприкосновение с данным цветом, т. е. заставим его воспринимать то, с чем мы желаем его ознакомить. Такой способ ознакомления с известным понятием называется указанием. Указание употребляется во всех случаях, когда нам приходится знакомить с предметами непосредственного восприятия.

2) Описание употребляется при ознакомлении с индивидуальными предметами или при ознакомлении со свойствами, принадлежащими какой-либо вещи. В таком случае приводятся возможно точно и полно признаки этой вещи, напр., описание

35

 

 

Днепра у Гоголя, Рейнского водопада у Карамзина и т. п. В ботанике описывается строение того или иного цветка, процесс опыления и т. п., в химии описывается та или иная реакция.

3) Характеристика приводит выдающиеся признаки какого-либо предмета или явления. Если нам нужно познакомить с тем, что такое «воображение построительное» и «воображение воспроизводящее», то мы вместо определения предлагаем какую-нибудь существенную черту, присущую тому или другому виду воображения, когда мы, например, говорим, что для построительного воображения существенным является новизна сочетания,—а для воспроизводящего точность. Какое-нибудь свойство является характерным для того или другого лица: для воина мужество, для врача гуманность и т. п. Характерной особенностью семейства крестоцветных растений являются «цветы с четырьмя листочками чашечки и четырьмя лепестками венчика, расположенными крест-накрест, с двумя короткими и чехырьмя длинными тычинками».

4) Сравнение употребляется в том случае, когда мы знакомим с тем или иным понятием при помощи сравнения его с другими понятиями, похожими на него. Мы можем дать понятие о теплопрозрачности какого-либо тела при помощи сравнения ее со светопрозрачностью, например, если скажем, что теплопрозрачность по отношению к тепловым лучам есть то же самое, что прозрачность по отношению к световым лучам. Сравнение употребляется главным образом тогда, когда одно понятие уясняется при помощи другого понятия более ясного, напр., когда какое-либо абстрактное понятие уясняется при помощи какого-либо конкретного. Напр., «жизнь есть школа опыта». «Право есть воплощение нравственной идеи». «Совесть есть внутренний суд».

5) Различение употребляется в том случае, когда мы знакомим с, содержанием какого-либо понятия, указывая на то различие, которое существует между данным понятием и другими. Например, если мы говорим, что «энтузиазм» отличается от «фанатизма» тем, что он вызывается чем-либо благородным и не переходит за пределы умеренности.

Вопросы для повторения. Что такое содержание понятия? Что такое сложные и простые понятия? Какие понятия не могут быть определены? Что такое определение? Перечислите условия правильности определения. Какие определения будут слишком узкие и какие слишком широкие? Когда

36

 

 

определение делает круг? Почему признаки, входящие в определение, не должны иметь отрицательного характера? Назовите приемы, заменяющие определение, и укажите особенности каждого приема.

 

ГЛАВА 7-я.

О делении.

Задача деления. От процесса определения отличается процесс деления (divisio). Различие между ними заключается в том, что определение раскрывает содержание понятия, а деление раскрывает его объем. Задача деления заключается в том, чтобы указать все виды, совокупность которых составляет объем данного понятия. Так, напр., понятие «треугольник» мы могли бы делить следующим образом:

У нас было понятие треугольника А и мы перечислили все частные понятия: В, С и D, входящие в объем этого более общего понятия, которое относихся к ним, как род к своим видам.

То понятие, объем которого мы раскрываем, называется делимым (totum dividendum), а те виды, которые получаются от деления, называются членами деления (membra divisionis).

Основание деления. Когда мы производим деление рода на виды, то мы обращаем внимание на те признаки, которыми обладают одни виды и не обладают другие. Тот признак, который дает нам возможность разделить род на виды, называется основанием деления (fundamentum divisionis). Основанием вышеприведенного деления понятия треугольник была «величина углов» в треугольнике. Но можно это же самое понятие делить по какому-нибудь другому основанию; например, положить в основание деления «отношение сторон треугольника по величине». Тогда деление представится в следующем виде:

37

 

 

Процесс несколько усложняется, если полученные от деления виды в свою очередь делить на подвиды. (Этот процесс называется подразделением.) Так, напр., под понятия треугольник, именно тупоугольный треугольник (или какой-нибудь другой), можно в свою очередь подразделить на подвиды: равнобедренный и разносторонний; разумеется, деление и подразделение будут относиться к одному понятию.

Дихотомия. В процессе деления иногда употребляется прием, который называется дихотомией и который заключается в делении данного понятия А на противоречащие понятия  и не-b. Берем какое-нибудь понятие, которое нам надо разделить, например, понятие «человек»; выделяем в одну группу какой-нибудь из видов, заключающихся в этом понятии, например, вид «славянин», а в другую группу «не-славянин» относим все прочие виды. Затем с этим вторым отрицательным понятием поступаем точно таким же образом: подразделяем понятие «не-славянин» на две группы; в одну из них относим, например, подвид «германец», а в другую—все прочие остающиеся подвиды, соединяя их в одно понятие «не-германец»; затем с этим понятием поступаем точно так же, как и с предыдущим, и продолжаем наше деление до тех пор, пока оно не окажется исчерпанным.

Этот прием имеет тот недостаток, что оставляет каждый раз крайне неопределенной часть объема делимого понятия, именно ту часть, которая обозначается частицей не, но, с другой стороны, значительно облегчает самый процесс деления потому, что придает ему исчерпывающий характер, почему его иногда называют исчерпывающим делением. Что оно имеет исчерпывающий характер, можно объяснить при помощи след. примера. Если мы разделим всех обитателей Европы и Азии на расы арийскую, семитическую и туранскую, то может случиться, что впоследствии будут открыты какие-нибудь племена, которые не подойдут ни под одну из этих рас и которых мы не будем в

38

 

 

состоянии поместить в нашем делении, но этого не будет в том случае, если мы будем делить дихотомически.

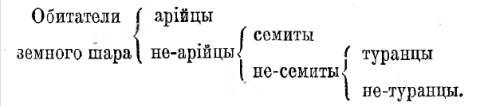
При таком делении всякое новое племя должно будет войти в последнюю группу, которая не будет ни арийской, ни семитской, ни туранской. В этом заключаются преимущества дихотомического деления.

Правила деления. Деление должно подчиняться следующим правилам:

1) Деление должно быть адекватно или соразмерно. Это значит, что если мы перечисляем по какому-нибудь основанию или принципу виды данного родового понятия, то мы должны точно перечислить все виды, не уменьшаая и не увеличивая их количество, т.-е. сумма видов должна равняться делимому роду.

Если при делении мы не перечислим всех видов, т.-е. если эта сумма будет меньше, то у нас получится деление неполное; если же мы в объем делимого понятия введем виды, которые в нем на самом деле не содержатся, то у нас получится деление слишком обширное, т.-е. указанная сумма будет больше. Например, положив в основание деления понятия «треугольник» величину его углов, мы могли бы получить такое деление:

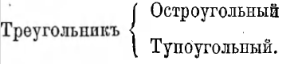
Ясно, что это деление неполное, ибо здесь не хватает одного члена деления, потому что в объеме понятия треугольник находится еще один вид, который при делении нами пропущен, именно прямоугольный треугольник.

Неполным было бы деление людей на порочных и добродетельных, деление научных теорий на истинные и ложные, потому что в этих делениях упускаются промежуточные ступени. Кроме людей порочных и добродетельных, есть люди, о которых нельзя сказать, что они порочны, но нельзя также сказать, что они добродетельны; кроме истинных и

39

 

 

ложных теорий, существуют еще теории частью истинные и частью ложные.

Обратная ошибка будет получаться в том случае, если мы, деля какое-либо понятие, вводим в его объем такой вид, который не входит в действительности в его объем. Если бы мы, например, разделили понятие «дерево» на «дуб», «ель», «фиалка», то очевидно, что вид фиалка относится к объему совсем другого понятия и что при делении понятия дерева он попал в число членов его неправильно.

2. Члены деления долины исключать друг друга. Это требование станет ясным, если мы возьмем для примера следующее деление:

Это деление неправильно, ибо понятие, например, «французские книги» и понятие «словари книги» не исключают друг друга: книга может быть и французскою, и словарем в одно и то же время. Или возьмем в пример также другое деление понятия «книги»:

Здесь один вид книг не исключает из своего объема других видов: полезная книга может быть в одно и то же время и понятною, и интересною. Ошибки как в первом, так и во втором из предложенных примеров деления произошли потому, что не было выдержано четвертое требование правильного деления, именно:

3) Деление должно иметь одно основание. При делении понятий чаще всего повторяется ошибка, заключающаяся в том, что в процессе деления меняется основание деления.

Произведем деление народов Европы:

40

 

 

Это деление неправильно, ибо мы, взявши сначала основанием деления, понятие «религия», затем меняем это основание на другое именно на понятие «национальности».

Или другой пример:

Это деление также неправильно, так как у нас здесь скрещиваются такие различные основания деления, как: число сторон, направление сторон, величина углов. Такое деление называется п е р е к р е с т н ы м .

Итак, четвертое условие правильности деления заключается в том, чтобы при последовательном перечислении видов делимого понятия было выдержано одно основание деления. Но следует заметить, что одно основание деления должно быть выдержано только при первом делении понятия; уже при вторичном делении, т.-е. при подразделении, основание деления должно измениться. Так, напр., если мы разделили понятие треугольник, взявши основанием деления величину углов, на такие виды, как остроугольный, прямоугольный и тупоугольный, то, желая далее продолжать деление какого-нибудь из этих членов деления, мы уже должны основание деления изменить. Так, понятие «остроугольный треугольник» мы можем делить еще далее, если возьмем основанием деления уже не величину углов, а отношение сторон повеличине.

4) Деление должно быть непрерывным, т.-е. при делении какого-либо понятия нужно переходить к ближайшему низшему роду, в проливном случае будет получаться то,  что называется скачком в делении. Если бы мы понятие «природа» разделили на 1) животные, 2) растения, 3) минералы, то в этом делении был бы слишком внезапный переход от понятия природы к понятиям «минералы», «животные». Чтобы исправить ошибку, следует вставить между понятием

41

 

 

«природы» и членами вышеприведенного деления еще два посредствующих звена, именно: понятие «мир органический» и «мир неорганический». Тогда деление приняло бы следующий вид:

Вопросы для повторения. Какова задача деления? Что называется делимым понятием? Что называется членами деления? Что такое основание деления? Что такое подразделение? Что такое дихотомия? Его преимущества и недостатки. Перечислите правила деления. Приведите примеры на каждое правило и укажите применение каждого правила.

 

ГЛAВА 8-я.

О суждении,

Познание и суждение. Если бы у нас были одни только представления и понятия, но не было бы их соединения или с в я з и, то могли ли бы мы сказать, что у нас есть познание? Конечно, нет. Познание может быть только в том случае, если мы имеем дело с истинностью или ложностью; а вопрос об истинности или ложности возникает только тогда, когда между понятиями устанавливается известная связь; это бывает именно тогда, когда мы судим о чем-нибудь. Например, когда я произношу слово «дом», то в понятии, выражаемом этим словом, нет ничего ни истинного, ни ложного. Когда же я говорю «дракон существует», «дракон имеет крылья», то я утверждаю нечто истинное или ложное. Следовательно, об истинности и ложности может быть речь только в том случае, когда мы имеем дело с суждением. Как мы видели в Психологии, суждение всегда имеет дело с какой-либо объективной реальностью.

Суждение есть известное умственное построение, но, будучи выражено в словах, оно называется предложением.

Грамматический анализ предложения. В предложении мы всегда высказываем что-нибудь относительно чего-нибудь. То, относительно чего мы высказываем, называется подлежащим, субъектом, а то, что мы о нем высказываем, называется предикатом, сказуемым. Типом простого предложения

42

 

 

является предложение «А есть В», «А не есть В». В этих предложениях А есть субъект (subjectum), В есть предикат (praedicatum); «есть» и «не есть» называется связкой (copula), потому что она служит для связывания подлежащего с сказуемым. Подлежащее обыкновенно обозначается символом S, а сказуемое—символом Р (начальные буквы слов subjectum, praedicatum).

Следует заметить, что когда мы говорим о суждении, то мы имеем в виду логическую точку зрения, когда же мы говорим о предложении, то мы имеем в виду грамматическую точку зрения.

[Форма суждений. Суждения, каковы бы они ни были, всегда представляют собою соединение субъекта с предикатом, но они видоизменяются в зависимости от изменения субъекта, предиката и связи между ними, Поэтому нам для ознакомления с возможными формами суждений следует рассмотреть возможные изменения субъекта, предиката и связи между ними.

I. Прежде всего рассмотрим особенность суждений в зависимости от изменения субъекта.

Субъект может быть или определенным, или неопределенным. Суждения с неопределенным субъектом суть так. назыв. безличные суждения, например: «светает», «мне скучно», «грустно», «больно». Между суждениями с определенным субъектом мы отличаем суждения единичные, частные и общие. Единичными суждениями называются такие, в которых подлежащим является какое-либо индивидуальное понятие. Например: «Ньютон открыл закон тяготения». Частное суждение — в котором подлежащим суждения является понятие, взятое в части своего объема, напр., суждение: «Некоторые S суть Р». Общие суждения—это те, в которых подлежащее служит для выражения класса вещей или явлений. Напр.: «Пауки суть суставчатоногие».

ΙΙ. Суждения по формам предиката можно разделить на повествовательные, описательные и объяснительные. Надо заметить, что субъект всегда является выражением понятия вещи, предмета, события, между тем как предикат служит для обозначения тех изменений, которые может подвергаться вещь.

43

 

 

Вещь мы рассматриваем как нечто пребывающее, постоянное, отличающееся от своих признаков именно тем, что она остается неизменной в то время, как эти последние изменяются. Это пребывающее принято называть субстанцией, а то, что в нем изменяется, принято называть акциденцией. Акциденция может выступать или в качестве состояния или свойства; в этом смысле предикат выражает ими состояние вещи, или свойство какой-либо вещи, но иногда он может выражать также и вещь.

В зависимости от этих особенностей предиката и суждения могут принимать толькочто указанные формы.

а) Повествовательные суждения содержат в своем предикате высказывание относительно событий, состояний, процессов или деятельности; предикат здесь всегда является понятием состояния, причем о повествуемых вещах высказываются состояния по преимуществу скоропроходящие. Эти суждения действительны только для определенного промежутка времени. Например: «Цезарь перешел Рубикон», «Роза в нашем саду цветет». «Этот огоньгорит». Эти суждения можно назвать повествовательными потому, что они употребляются по преимуществу в рассказах.

b) Описательные суждения. В описательных суждениях одному или многим предметам приписывается какое-нибудь свойство или множество свойств, при чем имеются в виду более или менее постоянные свойства. Субъектом всегда является какой-либо определенный предмет или вещь. Например, в суждении «огонь горяч» предикат выражает понятие свойства или признака субъекта. То же самое следует сказать относительно предикатов в следующих суждениях: «Снег бел». «Движения паровоза быстры». «Роза красива». «Кит дышит легкими». «Небо голубое». Обозначение суждений этого рода описательными про исходит вследствие того, что они применяются по преимуществу в описаниях.

c) Объяснительное суждение подводит какую-либо вещь под родовое понятие, причем в этом случае предикат выражает понятие вещи. Например, «Золото есть металл». «Кит есть млекопитающее». «Это есть железо». «Горение есть химический процесс». «Парабола есть коническое сечение».

44

 

 

III. Наконец, третий класс суждений это те суждения, в которых выражается определенное отношение между понятиями подлежащего и сказуемого. В них мы отличаем:

а) Суждения тождества. В суждениях этого рода понятиясубъекта и предиката имеют один и тот же объем, т.-е. в них подлежащее и сказуемое суть понятия равнозначащие. Например, «всякий равносторонний треугольник есть равноугольный треугольник»; «Петр I-й был первый русский император». В математике часто применяются суждения, выражающие тождество, именно сюда относятся суждения, которые выражаются уравнениями. Например:

(а+b)² =a² + 2ab + b²; а^т. а^п = а^т+^п.

b) Суждения подчинения совпадают с объяснительными суждениями. Здесь понятия субъекта и предиката не являются тождественными, так как их объемы отличаются друг от друга. Именно, здесь понятия с менее широким объемом подчиняются понятию с более широким объемом. Поэтому подобные суждения могут быть названы суждениями подчинения. Например: «Солнце есть неподвижная звезда». «Это есть правильный пятиугольник». «Собака есть домашнее животное».

c) Суждения отношения пространства, времени и причинности. В предложении «дом находится на улице» дело идет об известном пространственном отношении между «домом» и «улицей»; «находящийся на улице» образует содержание предиката. В суждении «Платон жил до Рождества Христова» предикатом является «живущий до Рождества Христова» и выражает собою временное отношение. «Солнце производит теплоту» (суждение причинности).]

Суждения существования. Если мы возьмем какое-нибудь суждение, в котором относительно S высказывается какое-либо Р, то в таком суждении мы по большей части не утверждаем прямо, что S существует вне человеческого мышления, потому что в этом случае только устанавливается известное логическое отношение между Sи Р. Если мы, напр., возьмем суждение: «ни одна часть окружности не есть прямая», то мы не ставим вопроса о том, существует ли что-либо вроде круга в строго геометрическом смысле. Если бы у нас даже не было убеждения в том, что такого рода круги

45

 

 

существуют, то все-таки мы могли бы произнести указанное суждение, потому что в них мы только устанавливаем известное отношение между подлежащим и сказуемым. Наоборот, такие суждения, как «Бог существует», «солнце существует», «существует любовь к родине, которая способна на великие жертвы», «существуют антиподы», имеют только ту цель, чтобы утверждать бытие или существование логического субъекта. Такие суждения, которые приписывают понятию субъекта только лишь существование, называются суждениями существования или экзистенциальными суждениями. Легко видеть, что слово «есть» в этих суждениях является не связкой, а предикатом и обозначает «существует».

Аналитические и синтетические суждения. Суждение, в котором мы относительно субъекта высказываем нечто такое, что в нем уже содержится, называется аналитическим. Например, в подлежащем суждения: «всякое тело протяженно», признак протяженности уже содержится. Мы не можем мыслить понятие «тело» без того, чтобы не мыслить его протяженным. Поэтому если мы говорим, что тело протяженно, то мы только раскрываем, анализируем то, что уже содержится в подлежащем. Оттого самое суждение называется аналитическим.

От аналитических суждений отличаются суждения, в которых предикат не находится в содержании субъекта, в которых предикат привносит нечто новое к содержанию субъекта. Такие суждения называются синтетическими. В них не раскрывается содержание подлежащего, а присоединяется нечто новое. Эти суждения называются также суждениями расширяющими познание, между тем как суждения аналитические называются суждениями объясняющими познание, потому что настоящее знание приобретается только благодаря синтетическим суждениям, аналитические же суждения только уясняют то знание, которое у нас уже имеется. Это разделение суждений принадлежит Канту.

Существовало мнение, что различие между суждениями синтетическими и аналитическими имеет абсолютный характер, т.-е. что некоторые суждения имеют всегда только аналитический характер, а другие суждения имеют только синодический характер. На самом же деле, если рассматривать суждения

46

 

 

с точкизрения их происхождения, то различие между синтетическими суждениями и аналитическими нужно считать относительным, потому что иногда признаки, которые мы считаем связанными аналитически, в действительности бывают связаны синтетически. Например, если мы произносим суждение «лев есть животное плотоядное», то это суждение должно быть признано, конечно, аналитическим, потому что признак плотоядности уже содержится в понятии лев. Но это суждение является аналитическим теперь, когда мы уже хорошо знакомы с содержанием понятия «лев». Когда же мы не были знакомы с содержанием понятия «лев», то это суждение имело характер синтетический, потому что тогда признак плотоядности присоединялся к понятию «льва». От постоянного совместного употребления понятия «лев» с признаком плотоядности это суждение сделалось аналитическим.

В английской логике этому разделению суждений на аполитические и синтетические до некоторой степени соответствует разделение предложений на словесные и реальные. Д. С. Милль следующим образом разъясняет различие между словесными предложениями и реальными. Словесные предложения это те, в которых содержание предиката заключается частью или целиком в содержании субъекта; словесное предложение утверждает о вещи только то, что мы уже предполагали, когда мы произносили название этой вещи; поэтому словесные предложения только раскрывают понятие подлежащего. Например, предложение «человек есть животное» есть предложение словесное, потомучто «животное» входит частью в содержание понятия «человек». Из этого ясно, что словесные предложения не утверждают чего-либо о вещах, но они нам дают знать только лишь о значении имен. Реальные предложения это те, в которых содержание предиката не составляет никакой части содержания субъекта. Предложение «три угла треугольника, вместе взятые, равны двум прямым» есть предложение реальное, потому что понятие субъекта (три угла треугольника) не содержит в себе понятия предиката (равенство двум прямым).

Но, кроме приведенной в этой главе классификации суждений, существует еще одна классификация, с которой нам

47

 

 

необходимо ознакомиться, потому что она лежит в основе всех дальнейших логических построений.

Вопросы для повторения. Какое существует отношение между познанием и суждением? Какое различие между суждением и предложением? Что кладется в основу деления суждения? Какие существуют суждения в зависимости от изменения субъекта и какое между ними различие? Какие существуют суждения в зависимости от изменения предиката и какое между нимн различие? Какие существуют суждения отношения? Какие суждения называются суждениями существования? Какое различие между аналитическими и синтетическими суждениями?

 

ГЛАВА 9-я.

Деление суждений.

Деление суждений. В логике принято делить суждения с четырех точек зрения: 1) количества, 2) качества, 3) отношения и 4) модальности.

Количество суждения. Когда суждения рассматриваются с точки зрения количества, то обращается внимание на то, в каком объеме берется подлежащее, во всем объеме или в части, т.-е., другими словами, справедливо ли то, что утверждается сказуемым, по отношению к подлежащему, взятому во в с е м  объеме, или оно справедливо только по отношению к подлежащему, взятому в части объема. Если я говорю: «все растения живут», то в этом суждении предикат «живут» справедлив относительно всех  растений, относительно всего класса растений, относительно понятия растения, взятого во всем объеме. Если я скажу: «некоторые растения суть хвойные», то предикат «хвойные» справедлив только относительно части объема растения. Первые суждения называются общими, а вторые—частными.

Формула общего суждения:

Все S суть Р.

Формула частного:

Некоторые S суть Р.

От частных суждений нужно отличать так называемые единичные или индивидуальные суждения. Например, суждение «Гутенберг — изобретатель книгопечатания» есть единичное

48

 

 

суждение. Индивидуальные суждения обыкновенно относят к общим  суждениям, так как в них предикат относится к субъекту, взятому во всем объеме, или, другими словами, в  них предикат действителен по отношению ко всему объему субъекта. То же самое следует сказать относительно всяких суждений, в которых подлежащее выражается понятием единичной вещи. Возьмем в пример суждение: «самообладание есть добродетель». Очевидно, в этом суждении предполагается, что дело идет о всяком самообладании.

Качество суждения. С точки зрения качества, суждения делятся на утвердительные и отрицательные. Формулы их таковы:

S есть Р.

S не есть Р.

Если мы предикат придаем субъекту, то это будет утвердительное суждение; если мы предикат отнимаем от субъекта, то суждение будет отрицательное. Например, суждение «люди пристрастны к самим себе» будет суждением утвердительным, потому что известный предикат мы приписываем субъекту (признаем входящим в содержание субъекта), а, например, суждение «люди не поддаются лести» будет отрицательным суждением, потому что предикат «поддаваться лести» мы отнимаем от людей, т. е. признаем не входящим в содержание субъекта «люди». Следовательно, с точки зрения качества мы определяем, придается ли предикат субъекту или обнимается от него.

Мы можем классы, получаемые от разделения суждений с точки зрения количества, соединить с классами, получаемыми от разделения суждений с точки зрения качества, и тогда мы получим суждения: обще-утвердительные и частно-утвердительные, обще-отрицательные и частно-отрицательные.

Формулы этих суждений будут следующие:

1) Обще-утвердительное суждение: «все Sсуть Р». Наприм.: «все люди боятся смерти».

2) Частно-утвердительное суждение: «некоторые S сути, Р». Наприм.: «некоторые люди имеют черный цвет кожи».

3) Обще-отрицательное суждение: «ни одно Sне есть Р». Напр.: «ни один человек не всеведущ».

4) Частно-отрицательное суждение: «некоторые S не суть Р». Наприм.: «некоторые люди не имеют черного цвета кожи».

49

 

 

Вот все четыре вида суждений. Для краткости их обозначения в логике принято употреблять следующие символы. Для обще-утвердительного суждения берут символ А, первую гласную глагола affirmo=утверждаю; для частно-утвердительного—I, вторую гласную того же глагола. Для обще-отрицательного—Е, первую гласную глагола nego = отрицаю; для частно-отрицательного О, вторую гласную того же глагола.

Таким образом символы суждений мы можем обозначить при помощи следующей таблицы:

А Все S суть Р

IНекоторые S суть Р

Е Ни одно S не есть Р

0 Некоторые S не суть Р.

Отношение между подлежащим и сказуемым. Суждения различаются также по отношению, какое устанавливается между субъектом и предикатом. С этой точки зрения суждения разделяются на категорические, условные и разделительные. Если я говорю «все люди смертны», то здесь я беру отношение между субъектом и предикатом безусловно. Это будет категорическое суждение. Категорическое суждение есть такое, в котором сказуемое утверждается или отрицается относительно субъекта без какого-либо ограничения во времени, в пространстве или вообще в каких-либо обстоятельствах. Когда я ограничиваю отношение каким-либо условием, тогда получается условное суждение; а когда в суждении оставляется место неопределенности, тогда получается разделительное суждение.

Категорические суждения. Схема категорического суждения:

S есть Р.

Пример: «земля вращается вокруг солнца».

Условные или гипотетические суждения. Схема условных суждений:

Если А есть В, то С есть D.

Пример условного суждения: «если дождь пойдет, то почва будет мокрая». Здесь во втором суждении сказуемое может быть приписано подлежащему при условии допущения истинности первого суждения. Другой пример условного суждения:

50

 

 

«если луна становится между солнцем и землею, то солнце затмевается». Из этих примеров можно видеть, что условие, которое поставляется в одном из суждений, делает отношение между подлежащим и сказуемым другого суждения не категорическим, а условным. Первое суждение принято называть основанием, а второе—следствием. В условных суждениях, таким образом, мы имеем два суждения, которые находятся друг к другу в отношении основания к следствию. Суждение, которое содержит условие, называется также предыдущим (antecedens); суждение, которое содержит следствие, называется последующим (consequens).

Разделительные суждения. Раздельные суждения имеют двоякий вид:

1) S ест или -А, или В, или С

2) или А, или В, или С есть Р.

Разница между этими двумя видами разделительных суждений, как это легко видеть, сводится к следующему. В первом случае возможны два, три или больше сказуемых при одном подлежащем; во втором возможны два, три или больше подлежащих при одном сказуемом. Эта возможность нескольких подлежащих при одном сказуемом, или нескольких сказуемых при одном подлежащем делает суждение неопределенным. Возьмем суждение: «треугольник есть или остроугольный, или тупоугольный, или прямоугольный»; в этом суждении одно подлежащее и три сказуемых.

Придавая подлежащему одно какое-нибудь сказуемое, мы исключаем все остальные. Вследствие этого, если одно суждение истинно, то остальные должны быть ложны. Если я говорю, что треугольник есть прямоугольный, то это значит, что он не остроугольный и не тупоугольный. Примером второго вида разделительных суждений может служить следующее суждение: «или Бэкон, или Шекспир, или человек, равный им по таланту, написал произведения, приписываемые Шекспиру».

Условия правительности разделительных суждений те же самые, что и условия правильности деления. Именно, они состоят в том, чтобы члены деления были приведены полностью и чтобы члены деления исключали друг друга. Против этого правила погрешают, наприм., такие суждения: «треугольники бывают или прямоугольные,

51

 

 

или тупоугольные»; «человек бывает или образованный, или бедный» (Какие ошибки?).

Условно-разделительные суждения. Из соединения условных суждений с разделительными образуются условно-разделительные суждения. Схема их:

Если А есть В, то C есть D или Е есть F,

или в более общей форме эту схему можно изобразить так:

Если есть А, то есть или а, или b, или с,

например: «если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии».

Модальность суждений, Остается рассмотреть четвертое отношение между суждениями, именно с точки зрения модальности. Сэтой точки зрения рассматривается, с какой квалификацией, т.-е. каким образом (cummodo), в суждении сказуемое приписывается подлежащему. Таких квалификаций можно признать три, а отсюда получается деление суждений по модальности на три разряда:

1) Проблематические — «S вероятно есть Р». «Илиада есть вероятно продукт; коллективного творчества». В проблематическом суждении соединение подлежащего со сказуемым и разъединение подлежащего от сказуемого выставляется просто, как известное предположение.

2) Ассерторические — «S есть Р». «Киев стоит на Днепре», «вода состоит из водорода и кислорода».

3) Аподиктические — «S необходимо должно быть Р». Например: «две прямые линии не могут замыкать пространства».

Анализируя приведенные примеры, мы видим, что проблематическое суждение характеризуется некоторым ограничением связи между подлежащим и сказуемым (утверждается вероятность, в о з м о ж н о с т ь); в ассерторическом суждении связь подлежащего со сказуемым утверждается решительно, без колебания (утверждается действительность какого-либо факта); в аподиктическом—утверждение получает характер необходимости.

На первый взгляд различие между суждениями ассерторическими и аподиктическими не совсем ясно. Кажется, что оба они обладают одинаковой достоверностью и что поэтому

52

 

 

между ними нет различия; на самом же деле между ними различие очень большое. Суждения ассерторические утверждают нечто действительно существующее, в этом смысле нечто вполне достоверное, но всегда можно мыслить и обратное тому, что утверждается в ассерторическом суждении; что же касается аподиктических суждений, то никоим образом нельзя мыслить противоречащих им суждений. Например, если я возьму ассерторическое суждение: «Киев стоит на Днепре», я могу мыслить Киев стоящим не на Днепре, а, например, на Неве; если же я возьму аподиктическое суждение: «две прямые линии не могут замыкать пространства», то я не могу мыслить иначе, я не могу мыслить, чтобы две прямые замыкали пространство. Аподиктическое суждение имеет характер необходимый. Другие примеры аподиктических суждений. «Если две величины равняются одной и той же третьей, то они равны между собою». «Если обвиняемый во время совершения преступления, которое имело место в х, находился в месте у, то он не совершил преступления».

Эти три признака: возможность, действительность, необходимость, и характеризуют собою три вида указанных суждений, т.-е. если в суждении выражается или возможность, или действительность, или необходимость, то получается или суждение проблематическое, или ассерторическое, или аподиктическое.

Но следует заметить, что некоторые логики отношение между аподиктическими и ассерторическими суждениями понимают несколько иначе. По их мнению, ассерторические суждения это такие, в истинности которых мы убеждены, но только не знаем, почему так должно быть, как мы утверждаем. В аподиктических суждениях эта причина нам известна. Например, суждение «Юпитер имеет четыре спутника»—ассерторическое. Суждение «скорость полета ружейной пули должна постепенно уменьшаться» (именно вследствие сопротивления воздуха)— аподиктическое.

Вопросы для повторения. Как делятся суждения по количеству и по качеству? На какие четыре класса делятся суждения и как они обозначаются? Как различаются суждения по отношению между подлежащим и сказуемым? Какова схема суждений категорических, условных, разделительных? Как делятся суждения по модальности и какое между ними различие? Каково отношение между ассерторическими и аподиктическими суждениями?

53

 

 

 

ГЛАВА 10-я.

Отношение между подлежащим и сказуемым. Объемы подлежащего и сказуемого.

Мы видели, что суждения бывают обще-утвердительные, обще-отрицательные, частно-утвердительные и частно-отрицательные. Теперь выясним отношение между подлежащим и сказуемьш во всех этих классах суждений.

Суждения А. Возьмем обще-утвердительное суждение: «все рыбы суть позвоночные» (все S суть P.). В этом суждении мы утверждаем, что всякая рыба входит в объем класса позвоночных, другими словами, что в класс вещей, который мы обозначаем при помощи сказуемого (позвоночные), входит целиком класс вещей, обозначаемых подлежащим. Но так как в классе позвоночных, кроме рыб, есть еще и другие животные, то объем класса позвоночных будет

 

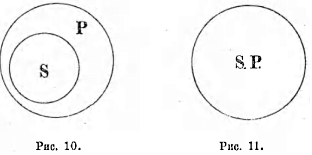
больше класса рыб. Если понятие S содержится в объеме понятия Р, то символически мы можем это представить при помощи круга S, который находится внутри круга Р. Поэтому те обще-утвердительные суждения, в которых объем подлежащего меньше объема сказуемого, можно символически изобразить, как это представлено на рис. 10.

Но если в обще-утвердительных суждениях подлежащее и сказуемое будут понятиями равнозначащими, то символ их будет иной. Возьмем пример: «все квадраты суть параллелограммы с равными сторонами и равными углами». В этом суждении S и Р суть понятия равнозначащие и, как таковые, совпадают друг с другом своими объемами. Поэтому мы не можем круг S поместить в середине Р, как это мы сделали в предыдущем суждении, а должны

54

 

 

представить отношение S к Р в виде двух совпадающих кругов (см. рис. 11).     -

Суждения Е. Возьмем обще-отрицательное суждение: «ни одно насекомое не есть позвоночное». В этом суждении мы отрицаем всякое, совпадение между подлежащим и сказуемым; один класс находится вне другого класса. Мы в мышлении совершенно отделяем класс подлежащего от класса сказуемого. Символически отношение S к Р в таких суждениях может быть обозначено посредством двух

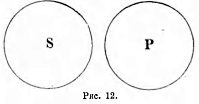
отдельно стоящих и несвязанных друг с другом кругов (см. рис. 12).

Суждения I. Возьмем частно-утвердительное суждение: «некоторые книги полезны». В этом суждении часть класса S входит в объем класса Р, т.-е. совпадает с классом Р. Если какая-нибудь часть S совпадает с Р, то круги S и Р должны иметь общую часть, т.-е. должны пересекаться. Символически отношение между подлежащим и сказуемым в частно-утвердительных суждениях можно изобразить так,

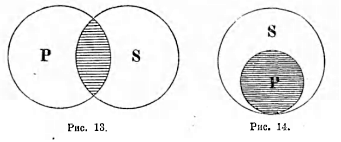
как это сделано на рис. 13. Та часть S, о которой утверждается Р, на рис. заштрихована.

Некоторые частно-утвердительные суждения можно символизовать иначе. Возьмем пример: «некоторые животные суть позвоночные». Если мы станем рассматривать объем понятий

55

 

 

«животные» и «позвоночные», то увидим, что последнее понятие подчинено первому, т.-е. в объем понятий «животные» входит, как часть, понятие «позвоночные». Поэтому символ такого частно-утвердительного суждения будет таков, как он изображен на рис. 14. Он показывает, что мы из S (животные) выделяем часть, которая и есть Р. Та часть S, о которой идет речь, на рис. заштрихована.

Суждения О. Возьмем частно-отрицательное суждение: «некоторые книги не суть полезны». Это суждение означает, что некоторые книги не входят в класс полезных вещей, другими словами, некоторая часть S не входит в объем Р. Если мы представим подлежащее и сказуемое суждение О в виде кругов (см. рис. 15), то эти круги должны иметь и общие и не общие

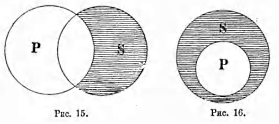
части, т.-е. они должны пересекаться. Заштрихованная часть круга означает, что об этой части субъекта идет речь в этом суждении и, именно, что она не входит в объем понятия Р, что она находится в н е понятия Р. Таким образом для суждения О мы получаем тот же символ, что и для класса суждений 1. Разница между их символами та, что в суждениях I мы обращаем внимание на то, что есть совпадающего между S и Р, а в суждениях О на то, что есть несовпадающего меледу ними.

К некоторым суждениям класса О применим другой символ. Возьмем, например, суждение: «некоторые змеи не имеют ядовитых зубов». Здесь опять понятие сказуемого подчинено понятию подлежащего. Так как «змеи, имеющие ядовитые зубы» (Р), составляют только часть класса змей, то Р входит как часть в объем понятия S (см. рис. 16). В суждении: «некоторые змеи не имеют ядовитых зубов», мы из объема S выделяем часть, которая ограничивается кругом Р. Эта часть S, которая находится в кругу Р, обозначает

56

 

 

тех змей, которые имеют  ядовитые зубы. Та часть, которая находится вне круга Р, будет обозначать змей, которые не имеют ядовитых зубов. Если мы заштрихуем ту часть круга S, которая находится вне Р, то мы покажем, о какой части всего класса идет речь.

Объемы подлежащего и сказуемого. Теперь нам следует рассмотреть суждения с точки зрения  объема их подлежащих и сказуемых. Если мы будем рассматривать суждения с этой точки зрения, то увидим, что в некоторых суждениях мы берем подлежащее или сказуемое во всем объеме, а в других не во всем. Если подлежащее и сказуемое берутся в суждениях во всем объеме, то говорят, что они распределены; если они взяты не во всем объеме, то говорят, что они не распределены.

В суждениях А подлежащее распределено, потому что в них предикат утверждается относительно в с е х  представителей того или другого класса, но сказуемое не распределено, что легко видеть из вышеприведенного примера: «все рыбы суть позвоночные». В этом примере мы приписываем известное свойство, в данном случае принадлежность к известному классу, всем  рыбам; что же касается до позвоночных, то мы приобретаем знание только о некоторой части их, но не о всех. Суждение А, поэтому, распределяет свое подлежащее, но не распределяет своего сказуемого.

Но в тех суждениях А, в которых подлежащее и сказуемое суть понятия равнозначащие, сказуемое взято во всем объеме. Напр., в суждении «все амальгамы суть ртутные сплавы».

В суждениях Е и подлежащее, и сказуемое распределены. Если мы возьмем суждение «ни одно насекомое не есть позвоночное», то в этом суждении мы утверждаем нечто как обо всех насекомых, что они не суть позвоночные, так и обо всех позвоночных, что они не суть насекомые. Из этого суждения мы узнаем, что ни один из предметов, находящихся в сказуемом, не может быть найден между предметами, находящимися в подлежащем. Таким образом обще-отрицательное суждение распределяет как подлежащее, так и сказуемое, потому что мы из него узнаем нечто как обо всем классе подлежащего, так и обо всем классе сказуемого.

57

 

 

В суждении I ни подлежащее, ни сказуемое не распределены. Если мы возьмем пример: «некоторые книги полезны», то мы из него не выносим никакого знания ни обо всем классе «книг», ни обо всем классе «полезных вещей». Из этого суждения мы только узнаем о некоторых книгах, что они полезны, но мы не узнаем, что входит во весь объем полезных вещей, т.-е. мы не узнаем, какие вещи полезны. Другими словами, из данного суждения мы ничего не узнаем обо всем классе полезных вещей. Мы об этом знаем из других источников, а не из данного суждения. Если же мы не узнаем ничего определенного относительно всего объема сказуемого частно-утвердительного суждения, то это значит, что эти суждения не распределяют своего сказуемого.

В суждении О подлежащее не распределено, ибо, когда мы говорим, что «некоторые животные не суть позвоночные», то мы берем подлежащее не во всем объеме, мы говорим о некоторых, а не обо всех животных. Сказуемое в суждении О распределено, так как мы S исключаем из всего объема сказуемого. Исключить вещь из какого-нибудь пространства, напр., из дома, значит удалить не из какой-нибудь части, но из всякой части, из всего пространства, из всего дома. Хотя часть животных входит в класс позвоночных, однако остальная часть исключается и притом из всех частей сказуемого.

На рис. 17 распределенность подлежащего и сказуемого обозначается при помощи более широких линий:

58

 

 

Случаи, когда субъект распределен или не распределен, не трудно помнить, потому что на это указывают «все», «некоторые», «ни один». Что же касается предиката, то вышеприведенная схема показывает, что отрицательные распределяют, а утвердительные не распределяют  своего предиката.

Вопросы для повторения. Изобразите символически отношение между подлежащим и сказуемым в суждениях A, Е, I, О. Когда говорится о подлежащем или сказуемом, что оно распределено? Какой признак для различения распределенности или нераспределенности? Рассмотрите суждения A, Е, I, О с точки зрения распределенности их подлежащих и сказуемых.

 

ГЛАВА 11-я.

О противоположении суждений.

Постановка вопроса. Мы видели, что существуют различные классы суждений в зависимости от того, какое им принадлежит количество и качество. Суждения, в которых одно и то же подлежащее и сказуемое, но которые имеют разные качества или количества или и то, и другое, будут противоположными друг другу. Например, суждение А и I, суждения Е и А противоположны друг другу.

Вопрос о противоположности суждений имеет важное значение. Если я, возражая кому-нибудь, не признаю истинности его утверждения, то я все-таки нечто могу признавать истинным. Например, кто-нибудь утверждает, что «все люди мудры», и я это отрицаю, то я в то же время сознаю, что я могу признать истинность суждения «некоторые люди мудры». Эти два суждения совместимы друг с другом. Если я утверждаю, что «все люди смертны», то я не могу в то же время признавать, что «некоторые люди не суть смертны». Одно суждение оказывается несовместимым с другим суждением. Отсюда возникает необходимость рассмотреть все суждения с точки зрения их противоположности, чтобы показать, какие суждения совместимы или несовместимы друг с другом.

Для выяснения этого вопроса мы воспользуемся схемой, известной под именем «логического квадрата» (см. рис. 18).

59

 

 

Схема эта наглядно показывает взаимное отношение суждений всех четырех классов.

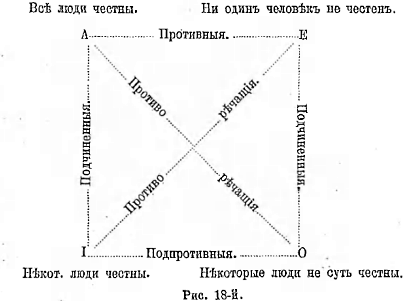
Возьмем квадрат и проведем в нем диагонали. У вершин четырех его углов поставим буквы А, Е, I, О, т.-е. символы четырех классов суждений. Возьмем какое-нибудь суждение и представим его в формах суждений всех четырех классов: А—«все люди честны», Е—«ни один человек не честен», I—«некоторые люди честны», О—«некоторые люди не суть честны».

Между суждениями А и О, Е и I существует отношение, которое называется противоречием. Эти суждения отличаются и по количеству, и по качеству.

Отношение между А и Е называется противностью. Эти общие суждения отличаются друг от друга по качеству.

Между А и I, Е и О есть отношение подчинения. Здесь суждения отличаются по количеству.

Между I и О отношение подпротивности. Здесь два частных суждения отличаются по качеству.

Рассмотрим каждую пару этих суждений в отдельности.

Противоречие (А—О, Е—I). Я высказываю суждение А «все люди искренни». Вы находите, что это суждение ложно. В таком случае вы должны признать истинным суждение О «некоторые люди не искренни». Если вы не допустите истинности этого последнего суждения, то вы не можете признать ложно-

60

 

 

сти моего утверждения. Следовательно, при ложности А—О должно быть истинным.

Возьмем суждение О «некоторые люди не суть смертны». Это суждение мы должны признать ложным, потому что мы признаем истинным суждение А «все люди смертны». Следовательно, при ложности О, А истинно.

Если я утверждаю, что «все люди смертны», и вы со мной соглашаетесь, т.-е. находите, что это суждение истинно, то вы должны будете признать, что при допущении истинности этого суждения нельзя признать истинности суждения О «некоторые люди не смертны», и, наоборот, если признать истинность суждения О—«некоторые люди не суть честны», то никак нельзя будет признать истинности суждения А— «все люди честны».

Таким образом из двух противоречащих суждений при истинности одного суждения другое оказывается ложным; при ложности одного суждения другое является истинным. Из этого следует, что из противоречащих суждений одно должно быть истинным, а другое ложным. Два противоречащих суждения не могут быть в одно и то же время оба истинными, но не могут быть и оба ложными.

Противность (A—Е). Если признать суждение А «все металлы суть элементы» истинным, то никак нельзя допустить, что «ни один металл не есть элемент». Следовательно, если А истинно, то Е ложно. Если мы признаем суждение Е «ни один человек не всеведущ» истинным, то мы, конечно, не будем иметь никакого права утверждать А «все люди всеведущи». Следовательно, если Е истинно, то А ложно. Таким образом из истинности одного из противных суждений следует ложность другого.

Но следует ли из л о ж н о с т и А истинность Е или из ложности Е истинность А? Отнюдь нет. В этом мы можем убедиться из следующих примеров. Возьмем суждение А «все бедняки порочны» и признаем, что это суждение ложно. Можно ли в таком случае утверждать Е «ни один бедняк не порочен». Конечно, нельзя, потому что в действительности может оказаться, что только некоторые бедняки не порочны, а некоторые порочны. Если я выскажу суждение Е «ни один алмаз не драгоценен» и вы станете отрицать истинность этого суждения, то сочтете ли вы себя в праве утверждать, что «все алмазы драгоценны»? Конечно,

61

 

 

нет. Отрицая мое утверждение, вы, в свою очередь, можете только утверждать, что «некоторые алмазы драгоценны», допуская в тоже время, что «некоторые алмазы не драгоценны». Следовательно, при ложности одного из противных суждений нельзя признать истинности другого, потому что между ними всегда может быть нечто среднее.

Итак, из двух противных суждений из истинности одного следует ложность другого, но из ложности одного не следует истинности другого; оба суждения не могут быть истинными (потому что, если одно истинно, то другое ложное), но оба могут быть ложными (потому что при ложности одного ложным может быт и другое).

Подчинение (A—I, Е—0). Если А истинно, то I тоже истинно. Например, если суждение А «все алмазы драгоценны» истинно, то истинно суждение I «некоторые алмазы драгоценны». Если Е истинно, то О тоже истинно. Если «ни один человек не всеведущ», то, конечно, это предполагает, что «некоторые люди не всеведущи». От истинности общих суждений, следовательно, зависит истинность частных.

Hoможно ли сказать, наоборот, что от истинности частных суждении зависит истинность общих суждений? Нельзя. В самом деле, если I истинно, то А может не быть истинным. Например, суждение I «некоторые люди мудры» истинно; будет ли вследствие этого истинным суждение А «все люди мудры»? Нет. Если О истинно, то Е может быть не истинно. Если мы признаем О «некоторые люди не искренни», то можем ли мы вследствие этого признать истинным суждение Е «ни один человек не искренен»? Конечно, нет.

Ложность общего суждения оставляет неопределенной ложность и истинность подчиненного частного. При отрицании истинности А мы не можем сказать, будет ли I истинным или ложным. При отрицании истинности Е мы не можем ни утверждать, ни отрицать О. Если мы, напр., отрицаем истинность А «все люди честны», то мы можем признавать истинным суждение I «некоторые люди честны». Если ми отрицаем суждение Е «ни один человек не есть мудр», то мы можем признавать истинность О «некоторые люди не суть мудры».

62

 

 

Ноложность частного приводит к ложности общего. Если I ложно, то А ложно. Если нельзя сказать: «некоторые люди всеведущи», потому что это ложно, то тем более нельзя сказать: «все люди всеведущи». Если О ложно, то Е ложно. Если нельзя сказать: «некоторые люди не суть смертны», то нельзя сказать, что «ни один человек не есть смертен», потому что, если чего-нибудь нельзя утверждать относительно части класса, то этого же тем более нельзя утверждать относительно всего класса.

Таким образом истинность частного суждения находится в зависимости от истинности общего суждения, но не наоборот; ложность частного приводит к ложности общего, но не наоборот.

Подпротивная противоположность (I-О). Если I истинно, то О может быть истинно. Если истинно суждение «некоторые люди мудры», то что сказать о суждении «некоторые (другие) люди не суть мудры»? Это суждение может быть истинным, потому что одни люди могут быть мудрыми, а другие немудрым. Если О истинно, тоI может быть истинно. Если мы скажем, что «некоторые люди не суть искренни», то мы в то же время можем предполагать, что «некоторые люди суть искренни»; одно суждение не исключает другого. Таким образом суждения I и О могут быть в одно и то же время истинными.

Если I ложно, то О истинно. Если нельзя сказать «некоторые люди всеведущи», то это происходит от того, что истинно противоречащее суждение Е «ни один человек не есть всеведущ», а если это суждение истинно, то истинно подчиненное суждение О «некоторые люди не суть всеведущи».

Если О ложно, то I истинно. Если ложно, что «некоторые люди не суть смертны», то это происходит от истинности противоречащего суждения «все люди смертны», а из истинности этого суждения следует истинность подчиненного суждения «некоторые люди смертны».

Следовательно, оба подпротивных суждения могут быть в одно и то же время истинными, но оба не могут быть ложными (потому что при ложности одного суждения другое является истинным).

Наиболыпая противоположность. Мы рассмотрели пары суждений противных и противоречащих. Спрашивается, ка-

63

 

 

кия суждения представляют наибольшую противоположность? Нужно думать, что таковыми являются суждения А и Е; между этими суждениями возникает наибольшая противоположность, когда мы их сопоставляем друг с другом. Если кто-нибудь скажет: «все книги содержат правду», и мы на это замечаем: «ни одна книга не содержит правды», то противоположность между первым суждением и вторым чрезвычайно велика. Не так велика будет противоположность в том случае, если на утверждение «все книги содержат правду», мы заметим, что «некоторые книги не содержат правды». Из этих примеров видно, что противоположность между А и Е больше, чем между А и О, т.-е. несогласие больше в первом случае, чем во втором. Таким образом наибольшая противоположность содержится в суждениях противных. Эха противоположность называется диаметральной.

Но хотя наибольшая противоположность существует между суждениями противными, однако при опровержении суждений обще-утвердительных и обще-отрицательных гораздо удобнее пользоваться суждениями противоречащими, а не противными, потому что гораздо меньше риска в утверждении I или О, чем в утверждении А или Е. Положим, кто-нибудь утверждает: «все книги полезны». Это утверждение можно отвергнуть, показав, что «ни одна книга не полезна», но можно отвергнуть, показав, что «некоторые книги не полезны». Этот второй способ опровержения предпочтительнее по следующей причине. В самом деле, если мы покажем, что «некоторые книги не полезны», то этого вполне достаточно для того, чтобы отвергнуть положение «все книги полезны». Между тем гораздо легче показать бесполезность только некоторых книг, чем показать, что ни одна книга не полезна. Гораздо меньше риска утверждать О, чем утверждать Е. По этой причине мы редко опровергаем общеутвердительные суждения при помощи обще-отрицательного, по гораздо чаще при помощи противоречащего частно-отрицательного. То же самое справедливо относительно другой пары противоречащих суждений.

Все сказанное выше об отношении суждений можно изобразить при помощи след. таблицы:

64

 

 

Эту таблицу учащийся не должен знать наизусть, но должен уметь ее вывести.

Вопросы для повторения. Какие суждения называются противоположными? Изобразите логический квадрат. Какие суждения называются противоречащими? Какое отношение противоположения существует между противоречащими суждениями? Какие суждения противные? Какое отношение противоположения существует между противными суждениями? Какие суждения называют суждениями подчинения? Какое отношение противоположения существует между суждениями подчинения? Какие суждения называются суждениями подпротивными? Какое отношение противоположения существует между суждениями подпротивными? Между какими суждениями существует наибольшая противоположность? Почему обще-утвердительное суждение лучше опровергать частно-отрицательным, чем обще-отрицательным?

 

ГЛАВА 12-я.

О законах мышления.

Понятие закона мышления, Под законами мышления понимаются такие законы, которым наше мышление должно подчиняться для того, чтобы оно было логическим, т.-е. истинным. Если сказать, что существуют такие законы, которым должно подчиняться мышление для того, чтобы сделаться истинным, то многим кажется, что нужно только знать, в чем заключаются эти законы, и применять их в процессе мышления для того, чтобы избежать ошибок мышления. Но такое мнение совершенно несправедливо, потому что так называемые законы мышления не суть законы, которые мы должны применять сознательно, преднамеренно, а это—законы, которыми мы пользуемся бессознательно.

Так как преднамеренное пользование законами мышления невозможно, то многие думают, что эти законы не имеют никакого практического значения для нашего мышления. По их мнению, они могли бы иметь значение только в том случае, если бы мы могли ими пользоваться для достижения

65

 

 

истины, а раз они такой цели служить не могут, то их следует отвергнуть, как совершенно бесполезные,

Чтобы определить действительное значение законов мышления, нам следует вспомнить то, что было сказано выше о различии между психологией и логикой. Мы видели, что психология, как и естественные науки, имеет целью описывать процессы мышления так, как они совершаются в действительности. В этом смысле естествознание формулирует общие положения, которые и называют законами природы; таким же образом и психология формулирует общие положения, служащие для выражения того, как совершается мышление, и эти общие положения можно назвать законами мышления. Логические законы мышления не поставляют своею целью изобразить, как совершается мышление вообще, но имеют целью изобразить, как должно совершаться то мышление, которое приводит и достижению истины. Поэтому законы мышления мы должны называть законами мышления не в том смысле, в каком обыкновенно закон природы называется законом, именно как формулирование того, что совершается фактически, но они суть законы в том смысле, что представляют собою известные требования, нормы, которым мысль наша должна подчиняться; мысль, чтобы быть правильной, должна следовать этим нормам, этим требованиям.

Обыкновенно признают четыре закона мышления, именно: «закон тождества», «закон противоречия», «закон исключенного третьего» и «закон достаточного основания».

Закон тождества. Закон тождества можно формулировать: „А есть A“, т.-е. всякий предмет есть то, что он есть. На первый взгляд кажется, что эта формула содержит в себе нечто само собою разумеющееся и потому практически не имеющее никакой цены. Но в действительности этот закон содержит весьма важное требование, именно чтобы в процессе нашего мышления каждая мыслимая вещь, или представление мыслимой вещи, которое мы обозначим символически при помощи А, сохраняло свое тождество. Если в нашем мышлении возникает представление какой-либо вещи (А), то оно и в дальнейших процессах мышления должно мыслиться с тем же содержанием, с каким мыслилось вначале. То, что мы мыслим в данный момент о той или другой вещи, мы должны мыслить и спустя известное

66

 

 

время, т.-о. мы должны мыслить с тем же самым содержанием, с каким мыслили раньше. Логическая мысль не могла бы осуществиться, если бы я, высказавши, что А есть В, при повторении этого суждения думал уже не об A, а о чем-нибудь другом. Если бы я, например, высказывая суждение: «поваренная соль состоит изхлора и натрия», думал о поваренной соли, при повторении же суждения стал думать о какой-нибудь другой соли, то процесс мышления привел бы меня к ложным результатам. Необходимо, чтобы я вторично, при повторении суждения «поваренная соль состоит из хлора и натрия», думал именно о поваренной соли, а не о какой-либо другой соли. Нужно, чтобы в процессе мышления каждая мыслимая вещь оставалась тождественной самой себе. Без соблюдения этого требования не может осуществиться логическое мышление, т.-е. истинное мышление.

Таким образом, по закону тождества, все то,  что мы мыслим, должно оставаться тождественным самому себе. Этот закон применяется, главным образом, к понятиям и представлениям. Они в процессе мышления должны оставаться тождественными самим себе, иначе будет нарушена правильность мышления.

Когда же мы начинаем соединять представления, другими словами, когда мы начинаем составлять суждения, то является необходимость применять еще три закона, именно: закон противоречия, закон исключенного третьего и закон достаточного основания.

Закон противоречия. Закон противоречия формулируется так: „А не может в одно и то же время быть В и не-B“, или: „Из двух суждений, из которых одно утверждает то, что другое отрицает, одно должно быть ложным". Смысл этого закона заключается в том, что ничто не может в одно и то же время, в одном и том же отношении иметь противоречащие качества. Мы, например, никак не можем себе представить, чтобы бумага была в одно и то же время и белая, и не-белая, напр., красная; мы никак не можем себе представить, чтобы дом в одно и то же время был и большим, и не-большим. Ни одно качество не может в одно и то же время и присутствовать, и отсутствовать. Вещь, совмещающая в себе противоречащие

67

 

 

качества, невозможна, да и суждение, которое заставляет нас мыслить присущность противоречащих качеств какой-либо вещи, будет ложным. Таким образом, закон противоречия требует, чтобы мы одной и той же вещи, в одно и то же время, в одном и том же отношении не приписывали противоречащих предикатов В и не-В.

Закон исключенного третьего. Закон исключенного третьего формулируется следующим образом: „при двух суждениях, из которых одно утверждает то, что другое отрицает („А есть B“ и „А есть не-B“), не может быть третьего, среднего суждения“.

Закон исключенного третьего лучше всего может объяснить, если сказать, что, согласно этому закону, о всяком качестве вещи мы можем только утверждать, что оно или принадлежит вещи или не принадлежит; в этом случае не может быть ничего третьего, среднего, что-либо третье в этом случае исключается. Когда мы приписываем какой-либо вещи какой-либо предикат, то мы можем приписывать только или В или не-В. Вещь должна быть или черной или не-черной. Растения могут быть или хвойные или не-хвойные; животные могут быть или позвоночные или не-позвоночные; третьего ничего быть не может (tertium non datur).

Закон достаточного основания. Четвертый закон мышления называется «законом достаточного основания» (lex rationis sufficientis). Этот закон обыкновенно определяется так: „мы все должны мыслить на достаточном основании“, т.-е. всякая мысль, всякое суждение должно иметь определенное логическое обоснование. Ближе это можно так пояснить. Если у нас есть суждение, истинность которого для нас не непосредственно очевидна, то мы должны найти основание(ra­tio) для этого суждения, мы должны дать логическое обоснование его. Но что такое логическое обоснование?

Мы видели при рассмотрении условных суждений, что называется основанием и что называется следствием, ипотому для нас должно быть понятно, что значит, что «мысль должна иметь известное обоснование». Если у нас есть какая-нибудь мысль, которая является причиной другой мысли, то мы говорим, что первая мысль обосновывает вторую мысль. С другой стороны, если у нас возникает какая-либо мысль, то мы всегда стараемся найти ту мысль,

68

 

 

которая является ее причиной, ее обосновывает, благодаря которой она только и может существовать. Мы видели в первой главе, что все положения должны быть сводимы на непосредственно очевидные положения; такое сведение предполагает, что между суждениями есть связь такого рода, что одни суждения опираются на другие, обосновываются другими. Например, если мы говорим, что «погода изменится», потому что барометрическое давление падает, то суждение: «барометрическое давление падает», является основанием для суждения: «погода изменится». Если мы находим, что «треугольник имеет две равных стороны», то это суждение есть основание для суждения: «два угла данного треугольника равны».

Когда одна мысль является причиной другой мысли, то. говорят, что между ними есть отношение основания и следствия. Когда какое-либо событие является причиной другого события, то говорят, что между ними есть отношение «причины» и «действия». Обыкновенно в логике основание и причина обозначаются одним и тем же термином ratio; но только основание называют ratio cognoscendi, а причину называют ratio fiendi. Чтобы видехь разницу между этими двумя ratio, везьмем пример. Я произношу суждение: «в комнате сделалось теплее». Логическое обоснование этого суждения может находиться в суждении: «ртуть термометра расширилась». Причинное обоснование теплоты комнаты получится в том случае, если мы скажем: «затопили печку, и оттого в комнате сделалось теплее».

Формальный характер законов мышления. Рассмотренные нами законы мышления в логике имеют такое же значение, какое в математике имеют аксиомы. Они так же непосредственно очевидны, как эти последние, как например, аксиомы: «целое больше части», «между двумя точками можно провести только одну прямую».

Эти законы называются также формальными законами мысли, потому что они не касаются содержания мысли. Закон тождества не указывает, какие именно представления, понятия, суждения должны оставаться тождественными; закон противоречия также не указывает, какие именно мысли не должны сами себе противоречить; закон исключенного третьего ничего не говорит, между какими именно противоречащими

69

 

 

суждениями не может быть ничего третьего, но они не говорят этого потому, что их утверждение справедливо по отношению ко всякому представлению, ко всякому суждению: всякая мысль должна подчиняться этим законам, совершенно так, как алгебраические формулы не показывают, в применении к каким числам они справедливы, и именно потому, что в них можно подставлять какие угодно числа или величины.

Вопросы для повторения. Что называется законами мышления? Какое отличие законов мышления от законов природы? Какие существуют законы мышления? Как формулируется закон тождества? Как формулируется закон противоречия? Объясните применение закона противоречия. Как формулируется закон исколоченного третьего? Объясните применение закона исключенного третьего. Как формулируется закон достаточного основания? Какое различие между основанием и причиной? Почему законы мышления называют формальными законами?

 

ГЛАВА 13-я.

О непосредственных умозаключениях.

Определение умозаключения. Теперь мы рассмотрим умозаключение или рассуждение, которое представляет собою наиболее совершенное логическое построение. Умозаключение получается из суждений, и именно таким образом, что из двух или больше суждений с необходимостью выводится новое суждение. Это последнее обстоятельство, именно выведение нового суждения, особенно характерно для процесса умозаключения.

Итак, умозаключение есть вывод суждения из других суждений, которые в таком случае называются посылками, или предпосылками (praemissae). Вообще умозаключение является результатом сопоставления ряда посылок. Но есть вид умозаключений основывающихся на одной посылке; это так называемые умозаключения в несобственном смысле или умозаключения непосредственные. Например, у меня есть суждение: «ни один металл не есть сложное тело»; имея такое суждение, я могу сделать вывод, что «ни одно сложное тело не есть металл». Это есть непосредственное умозаключение. Умозаключение это есть потому, что, допустив одно суждение, мы из него выводим  другое.

70

 

 

В зависимости от числа посылок умозаключения делятся на две группы: 1) умозаключения в несобственном смысле или непосредственные умозаключения; 2) умозаключения в собственном смысле. К этой последней группе относятся следующие виды умозаключений: 1) индукция, 2) дедукция, 3) аналогия и т. п.

Непосредственные умозаключения. Непосредственные умозаключения делятся на следующие группы:

I. Умозаключения противоположности, которые в свою очередь делятся на пять групп:

1) Умозаключение    от подчиняющего к подчиненному (ad subordinatam). Мы знаем, что если дано обще-утвердительное суждение, например, «все люди подвержены заблуждениям», то от истинности его мы заключаем е истинности частно-утвердительного: «некоторые люди подвержены заблуждениям». Как легко видеть, это есть умозаключение от суждения подчиняющего к суждению подчиненному. Мы рассмотрели случай умозаключения от А к I; к этой же группе относятся умозаключевия от Е к 0.

2) Умозаключение от подчиненного к подчиняющему (ad subordinantem). Например, дано частно-утвердительное суждение: «некоторые лошади суть животные плотоядные», от ложности его заключаем к ложности общеутвердительного: «все лошади суть животные плотоядные».

3) Ad contradictoriam (A—О, Е—I). От ложности обще-утвердительного суждения: «все люди читают газеты», заключаем к истинности частно-отрицательного:—«некоторые люди не читают газет». Подобное же отношение возможно между суждениями Е и I. (Перечислите, какие именно возможны случаи умозаключения ad contradictoriam.)

4) Ad contrariam (A—E). От истинности обще-утвердительного суждения «все растения суть организмы» заключаем к ложности противного суждения: «ни одно растение не есть организм». Случаев умозаключения ad contrariam два: от истинности А к Е и от истинности Е к А.

5) Ad sub contrariam(I—О). Дано частно-утвердительное суждение: «некоторые люди всеведущи»; от ложности этого суждения заключаем к истинности частно-отрицательного:—«некоторые люди не суть всеведущи».

Обратимся к следующей группе непосредственных умо-

71

 

 

заключений, получающейся при изменении суждений, которое называется превращением,

II. Превращение (obversio). Этот процесс состоит в изменении формы суждений: утвердительные суждения превращаются в отрицательные и наоборот; при этом смысл суждения не изменяется.

Например, возьмем суждение, данное нам в утвердительной форме: «эти ученики прилежны». Это суждение можно превратить в равнозначащее ему суждение отрицательное. Для этого должно поставить перед связкой и сказуемым отрицание. Тогда у нас получится суждение: «эти ученики не суть не-прилежны».

Отрицательное суждение превращается в равнозначащее ему утвердительное тем, что отрицание от связки переносят на сказуемое. Например, «ученики не суть прилежны»; превращение этого отрицательного суждения дает утвердительное суждение: «ученики суть неприлежны». Принято говорить, что второе суждение есть вывод из первого.

Вот, например, превращения одних суждений в другие:

Превращение А. «Все. металлы суть элементы» превращается в Е «все металлы не суть не-элементы или «ни один металл не есть не-элемент», или «ни один металл не есть сложное тело».

Превращение Е. «Ни один человек не бывает совершенен» превращается в суждение А «все люди суть несовершенны».

Превращение I. Суждение «некоторые люди надежны» превращается в суждение О «некоторые люди не суть ненадежны».

Превращение О. Суждение «некоторые люди не суть надежны» превращается в суждение I «некоторые люди суть ненадежны».

Таким образом мы видим, что есть определенный закон превращения одних суждений в другие: А всегда превращается в Е, Е в А, I в О, О в I.

Общая схема превращения:

72

 

 

Третий класс непосредственных умозаключений называется обращением (conversio).

III. Обращение (conversio). В этом процессе происходит перемещение подлежащего на место сказуемого и наоборот.

Попробуем обратить суждение А «все птицы суть животные» по только что указанному способу. Тогда получится суждение: «все животные суть птицы», но это неверно, так как в класс животных входят и рыбы и млекопитающие; следовательно, есть животные, которые не суть птицы. Ошибка в этом обращении получилалась вследствие того, что не принято в соображение то обстоятельство, что в обще-утвердительных суждениях сказуемое не распределено, а потому при обращении сказуемое нужно брать не во всем объеме. Поэтому суждение «все птицы суть животные» обращается в суждение «некоторые животные суть птицы». Необходимость изменения количества сказуемого в процессе обращения обще-утвердительного суждения можно сделать ясной при помощи схемы (рис. 10), которая указывает отношение объемов подлежащего и сказуемого. Подлежащее «птицы» (S) составляет только часть объема предиката Р; поэтому при обращении предикат нужно взять не во всем его объеме. Такое обращение, когда суждение изменяет свое количество, называется обращением посредством ограничения (Conversio per limitationem или peraccidens).Таким образом суждение А обращается в I.

Но иногда подлежащее и сказуемое обще-утвердительного суждения суть понятия разнозначащие, т.-е. имеют одинаковый объем, то суждение после обращения сохраняет свое количество; тогда говорят, что обращение происходит чисто. Например, суждение «все обезьяны суть четверорукие» обращается в суждение «все четверорукие суть обезьяны». Такое обращение называется простым или чистым обращением (Conversio simplex).

Суждение I обращается чисто. Например, суждение «некоторые металлы драгоценны» обращается в суждение «некоторые драгоценные вещества суть металлы».

Суждение Е обращается в суждение Е также чисто. Например, суждение «ни один честный свидетель не подкуплен» обращается в суждение «ни один подкупленный человек не есть честный свидетель».

73

 

 

Но возьмем суждение О: «некоторые люди не суть богаты»; по обращении должно было бы получиться: «все богатые не суть люди». Но это не может быть потому, что в обращенном суждении сказуемое взято во всем объеме, между тем как в обращаемом суждении оно было взято не во всем объеме. Частно-отрицательное суждение вообще не обращаемо, а именно оттого, что в обращенном суждении должно получиться отрицательное суждение, след. сказуемое в нем должно быть распределено, между тем в обращаемом суждении оно в качестве подлежащего частного суждения не распределено.

Часто говорят, что эта теория обращений не имеет никакого смысла, но в действительности она имеет практическое значение. При обращении обще-утвердительных суждений у нас всегда имеется стремление обращать их без ограничения. Например, когда произносят суждение «все великие люди имеют большие черепа», то есть тенденция думать также, что «все, имеющие большой череп, суть великие люди».

* IV Противопоставление. Четвертый класс непосредственных умозаключений называется противопоставлением. Это собственно есть соединение превращения с обращением. В процессе противопоставления мы сначала производим превращение какого-либо суждения, а затем превращенное суждение обращаем. Например, возьмем суждение А: «все металлы суть элементы», произведем превращение, получится суждение: «все металлы не суть не-элементы». Обращая же это суждение, получим Е «все неэлементы не суть металлы», или, что то же, «все сложные тела не суть металлы».

Возьмем противопоставление обще-отрицательного суждения Е «ни один лентяй не заслуживает успеха». Это суждение превращается в суждение «все лентяи суть не заслуживающие успеха». Это суждение в свою очередь при обращении дает: «некоторые люди, не заслуживающие успеха, суть лентяи».

Наконец, возьмем противопоставление частно-отрицательного суждения О: «некоторые несправедливые законы не отменены». Это суждение превращается в I «некоторые несправедливые законы суть неотмененные законы»; а это суждение при обращении дает: «некоторые неотмененные законы суть несправедливы». Суждение I, как это легко понять, не допускает противопоставления.

74

 

 

Таблица противопоставления:

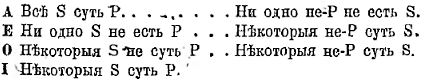
Вопросы для повторения. Как определяется умозаключение? Какие виды умозаключений мы различаем? Какие умозаключения называются непосредственными? Какие умозаключения называются умозаключениями подчинения? Противоположности? Что такое превращение? Как превращаются суждения A, Е, I, О? Что такое обращение? Как обращаются суждения А, Е, I, О ? Что такое противопоставление?

 

ГЛАВА14-я.

Дедуктивные умозаключения, Силлогизм.

Определение силлогизма. Мы рассмотрели непосредственные умозаключения, теперь перейдем к рассмотрению посредственных умозаключений и из них прежде всего рассмотрим дедуктивные умозаключения. Дедуктивные умозаключения принимают формы силлогизма. Силлогизм есть такая форма умозаключения, в которой из двух суждений необходимо вытекает третье, при чем одно из двух данных суждений является обще-утвердительным или обще-отрицательным. Силлогизм, таким образом, представляет собою умозаключение от общего. Полученное суждение ни в коем случае не будет более общим, чем суждение, из которых оно выводится.

Например, нам даются два суждения:

Все растения суть организмы

Сосны суть растения.

Из них следует, что „Сосны суть организмы“.

Этот пример показывает, что если нам даются два суждения, из них необходимо получается новое суждение. Мы не входим в рассмотрение того, истинны ли эти суждения или нет, но раз только мы допустим их, то тотчас же необходимо следует новое суждение.

Части силлогизма. Данные суждения называются предпосылками или посылками (praemissa), а новое суждение, которое получается из сопоставления посылок, называется заключением (conclusio). Те понятия, которые входят в заключеиие и пред-

75

 

 

посылки, называются терминами (termini), Подлежащее заключения (сосны) называется меньшим термяном (terminus minor)? сказуемое заключения (организмы) называется большим термином (terminus major), а термин (растение), который не входит в заключение, называется средним термином (terminus medius).

Обозначение терминов большими или меньшими находится в зависимости от того, какой объем  им присущ в одном из типичных случаев силлогистического вывода, как в только что приведенном. Самый больший объем приходится на долю сказуемого (организма), самый меньший—на долю меньшого термина, подлежащего заключения (сосны), а средний — на долю среднего термина (растение), который не входит в заключение. Это наглядно обнаруживается, если изобразить отношение между терминами схематически. На рис. 19 S  обозначает меньший термин, М—средний, Р—больший. 

Средний термин называется средним также потому, что он служит посредствующим связующим элементом между большим и меньшим термином. Средний термин служит для сравнения большого термина с меньшим. Сами по себе эти термины не могут быть сравниваемы.

Сравнение может происходить через посредство среднего термина. Мы не могли бы связать термина «сосны» с термином «организмы», если бы у нас не было термина «растения», который связывается с одной стороны с термином «организм», с другой стороны с термином «сосны» и таким образом служит связующим звеном между термином «сосны» и термином «организмы».

Суждение, в которое входит бблыпий термин, называется большей посылкой; суждение, в которое входит меньший термин, называется меньшей посылкой.

Форма и материя силлогизма. В силлогизме нужно отличать материю от формы. Материя—это термины, которые имеются налицо. Форма есть связь, которая придается нами термины посылок. В силлогизме, как уже было сказано выше, мы можем не обращать никакого внимания на истинность или ложность посылок. Для нас важно только сделать

76

 

 

правильный вывод, совершить правильное умозаключение, правильдо связать больший термия с меньшим, а этс и есть форма силлогизма. Поэтому иногда посылки могут быть ложными, а заключепие будет все-таки истинным, как это можно видеть из следующего силлогизма, посылки которого состоят из очевидно ложных суждений.

Львы суть травоядные

Коровы суть львы

____________________

Коровы суть травоядные.

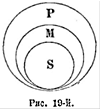Аксиома силлогизма. Силлогистическое умозаключение таково, что раз мы допустили посылки, то из них необходимо будет вытекать заключение. Но почему же происходит то, что при наличности известных посылок заключение вытекает из них необходимо? Такого рода отношение между посылками и заключением объясняется следующим положением: «если одна вещь находится в другой, а эта другая находится в третьей, то первая находится в третьей», или «если одна вещь находится в другой, а эта другая находится вне третьей, то и первая также находится вне третьей». Это положение, которое называется аксиомой силлогизма, можно иллюстрировать при помощи следующей схемы:

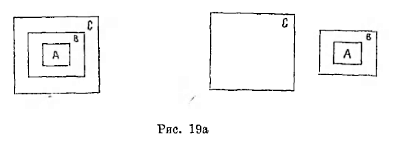
Если А находится в В, a В находится в С, то след. А находится в С. Далее, если А находится в В, но В находится вне С, то А также находится вне С.

Наиболее общая формула этой аксиомы называется в логике dictum de omni et de nullo. Полное выражение этой аксиомы будет: «quidquid de omni valet, valet etiam de quibusdam et de singulis. Quidquid de nullo valet, nec de quibusdam va­let, nec de singulis». Смысл этой аксиомы заключается в следующем. Все, что утверждается относительно целого класса, утверждается и относительно каждой вещи, которая содержится в этом клас-

77

 

 

се, и наоборот: все, что отрицается относительно целого класса, отрицается относительно всего, что содержится в этом классе. Это положение называется аксиомой, потому что оно очевидно; аксиомой же силлогизма оно называется потому, что на нем основывается необходимость вывода заключения силлогизма из данных предпосылок.

Правила силлогизма. Рассмотрим, какие правила мы должны соблюсти при построении силлогизма, чтобы он был правилен, или, другими словами, каким условиям должен удовлетворять силлогизм, чтобы заключение было правильно.

Первое правило:

1) Во всяком силлогизме должно быть не менее и не более трех терминов.

Если дается более трех терминов, то силлогистического соединения получиться не может. Если мы возьмем такой пример:

Все ораторы тщеславны

Цицерон был государственный человек,

то в данных двух суждениях четыре термина, и вывода сделать нельзя. Если бы второе суждение было: «Цицерон оратор», то можно было бы сделать вполне определенный вывод, потому что тогда в силлогизме было бы три термина.

Иногда в силлогизме бывает четыре термина, а на первый взгляд кажется, что их только три. Это происходит вследствие двусмысленности терминов.

Вот пример:

Лук есть оружие дикарей

Это растение есть лук__________

Это растение есть оружие дикарей.

Ошибка в этом случае происходит вследствие того, что средний термин в большей посылке употреблен не в том же смысле, в каком он употреблен в меньшей посылке. Таким образом в силлогизме вместо трех терминов получается четыре. Такая погрешность называется quaternio terminorum (учетверение терминов.)

Второе правило силлогизма формулируется следующим образом:

2) Во всяком силлогизме должно быть не более и не менее трех суждений.

78

 

 

Это оттого, что при трех терминах может быть только три суждения. В самом деле, если у нас есть три термина, два из которых должны входить в состав того или другого суждения, при чем одна и та же пара терминов не должна повторяться, то ясно, что из т р е х  терминов можно получить только три суждения.

3) Средний термин должен быть взят по крайней мере в одной из посылок во всем объеме.

Для пояснения этого правила возьмем пример:

Все французы суть европейцы

Все парижане суть европейцы.

Из этих двух посылок нельзя сделать никакого заключения. Но если бы средний термин мы взяли хоть в одной посылке во всем объеме, то заключение было бы возможно сделать. Например:

Все французы суть европейцы

Все европейцы суть культурны

След. все французы суть культурны.

Возьмем еще пример:

Все натуралисты наблюдательны

NN наблюдателен._______________

След. NN натуралист.

, Так как термин «наблюдательный» взят не во всем объеме, то в класс наблюдательных, кроме натуралистов, могут входить и историки, и художники и т. п. След. NNможет быть наблюдателен и в то же время находится вне круга натуралистов, как это можно видеть на прилагаемой схеме.

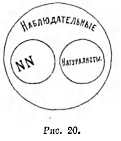
Если бы было сказано

Все наблюдательные люди суть натуралисты

NN наблюдателен_______________________

След. NN натуралист,

то такой вывод был бы правилен.

79

 

 

В первом случае средний термин ни в одной из посылок не взят во всем объеме. Вследствие этого получается неопределенность. Именно может случиться, что мы один раз берем одну часть среднего термина, а другой раз—другую, как это можно видеть на схеме. Между тем, если средний термин взят хоть один раз во всем объеме, то мы и в большей и в меньшей посылке будем иметь дело с одним и тем же.

Если вообще средний термин взят хоть в одной посылке во всем объеме, тогда имеется налицо то, что связывает больший термин с меньшим термином. Если же он не входит ни в большую посылку, ни в меньшую во всем объеме, то он не может выполнять своего назначения—быть соединительным звеном, потому что в таком случае больший или меньший термин относятся к чему-либо неопределенному, как в приведенном выше случае: NN может быть внутри круга натуралистов, но может быть и вне этого круга. Вследствие этого не может получиться определенного заключения. Поэтому средний термин хоть в одной из посылок должен быть взят во всем объеме.

4) Термины, не взятые в посылках во всем объеме, не могут быть и в заключении взяты во всем объеме.

Для пояснения этого правила возьмем следующий пример:

Все преступники застукивают наказания

Некоторые англичане суть преступники_

Все англичане заслуживают наказания.

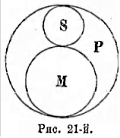Очевидная ошибка в этом силлогизме получается вследствие того, что мы в заключении термин «англичане» берем во всем объеме, между тем как в посылке этот термин взят не во всем объеме. Мы бы сделали правильно заключение, если бы сказали: «некоторые англичане заслуживают наказания».

Возьмем другой пример, где ошибка не так очевидна?

Все историки беспристрастны

Натуралисты не суть историки

Натуралисты не суть беспристрастны.

Чтобы видеть, правилен ли этот вывод, изобразим силлогизм символически (см. рис. 21). Историки (М) находятся в Р (беспристрастные). О натуралистахсказано, что они не

80

 

 

суть историки. Мы, следовательно, не имеем права помещать их в круге М; поэтому натуралистов мы можем поместить где угодно, лишь бы не в круге М, а если так, то, помещая S вне М, мы можем его поместить все-таки в кругу Р. Вследствие этого может оказаться, что «натуралисты беспристрастны». В большей посылке термин «беспристрастный»  взят не во всем объеме, так что историки должны составлять только ч а с т ь тех, которые беспристрастны, а потому мы не имеем права исключать из числа беспристрастных и натуралистов. Ошибка в этом силлогизме получилась оттого, что в большей посылке термин «беспристрастный», как сказуемое обще-утвердительного суждения, взят н е во всем объеме, между тем как в заключении, как сказуемое обще-отрицательного суждения, он взят во всем объеме. Другими словами, мы один раз говорим не обо всех, а другой раз обо всех. Такая ошибка называется ошибкой illiciti processi, недозволительное расширение большего термина, как в данном примере; недозволительное расширение меньшого термина мы имели в первом примере.

5) Из двух отрицательных суждений нельзя вывести никакого заключения.

Возьмем пример, чтобы пояснить это правило:

Химия не есть гуманитарная наука

Математика не есть химия.

 

 

Что следует из этих посылок? Обозначим (рис. 22) «химия» посредством М, «гуманитарные науки» посредством Р, «математика» посредством S; М должно быть вне Р, S должно быть вне М. Как легко видеть, средний термин в этом

81

 

 

силлогизме не связывает больший термин с меньшим, потому что оп находится вне большого и меньшего термина. Если М не соединено с Р, a S не соединено с М, то S не может быть соединено с Р, т.-е. через средний термин нельзя установить никакой связи между большим и меньшим термином.

6) Если одна из посылок отрицательна, то заключение должно быть также отрицательно, и наоборот, для получения отрицательного заключения необходимо, чтобы одна из посылок была отрицательна.

Возьмем пример:

Ни одно М не есть Р

Все S суть М.

Раз Р находится вне среднего термина М, то, очевидно, S, которое находится в М, не свяжется с Р, а потому получится отрицательное заключение.

Таким образом, если у нас есть две посылки, из которых одна отрицательна, то мы не можем сделать утвердительного заключения.

7) Из двух частных суждений нельзя сделать никакого заключения.

Это ясно из предыдущих правил. Предположим, что эти частные суждения будут I и I; тогда окажется, что средний термин в обеих посылках будет не распределен, как подлежащее и сказуемое частно-утвердительного суждения. Если мы будем стараться вывести заключение, то мы нарушим третье правило. В самом деле, пусть эти посылки будут:

Некоторые М суть Р

Некоторые S суть М.

В обоих этих суждениях средний термин не распределен. Следовательно, заключение не следует необходимо. Если мы возьмем суждение I и О, например:

Некоторые М суть Р

Некоторые S не суть М.

Так как здесь одна посылка отрицательная, то и сказуемое Р заключения должно быть распределено, между тем как в данных посылках Р, как сказуемое частно-утвердительного суждения, не распределено. След., попытка сделать заключение нарушала бы правило 4-е.

82

 

 

Наконец восьмое правило так формулируется:

8) Если одна из посылок есть суждение частное, то и заключение также должно быть частным.

Если мы желаем получить общее заключение в том случае, когда в силлогизме одна из посылок частная, то нарушается третье или четвертое правило.

В самом деле пусть мы имеем силлогизм:

Все М суть Р

Нек. S суть М

Все S суть Р.

В этом силлогизме нарушается правило 4-е.

Или пусть мы имеем силлогизм:

Нек. М суть Р

Все S суть М_____

Все S суть Р.

В этом силлогизме нарушается правило 3-е.

Вопросы для повторения. Как определяется силлогизм? Какие части мы различаем в силлогизме? Какое различие между формой и материей силлогизма? В чем заключается аксиома силлогизма? Перечислите правила силлогизма и объясните при помощи примеров их применение.

 

ГЛАВА 15-я.

Силлогизм. Фигуры и модусы силлогизма.

Возможные сочетания суждений в силлогизме. В предыдущей главе мы рассмотрели условия правильности силлогизмов. Рассмотрим теперь на примерах приложение этих правил. Мы будем брать по три суждения, которые могли бы составить силлогизм. Эти суждения должны быть или А, или I, или О, или Е. При чем само собой разумеется, что для образования силлогизма они могут комбинироваться самыми различными способами. Напр., мы могли бы иметь сочетание суждений ААО, ЕАI и т. п. Но мы должны исследовать, пользуясь вышеизложенными правилами, какие из этих сочетаний или соединений дают правильные силлогизмы.

Для того, чтобы решить вопрос, какие сочетания дают правильные силлогизмы, мы должно предварительно решить вопрос, какие вообще возможны сочетания. Для этого мы посту-

83

 

 

пим след. образом. Возьмем сочетания АА, AE, AI, АО 4 раза и прибавим к этим сочетаниям А, Е, I, J, получим:

Действуя аналогичным способом, мы можем получить 64 возможных сочетания.

Составивши полную таблицу таких сочетаний, мы рассмотрим, руководясь правилами, приведенными в прошлой главе, какие из этих сочетаний должны быть отброшены, как несоответствующие этим правилам, и какие из этих сочетаний должны быть оставлены, как дающие правильные силлогизмы.

Берем первое сочетание ААА. Это сочетание не противоречит всем 8 правилам.

Сочетание ААЕ противно 6-му правилу, потому что в заключении находится отрицательное суждение Е; а чтобы это было возможно, нужно, чтобы одна из посылок была суждением отрицательным, между тем в нашем силлогизме ААЕ обе посылки положительны. Следовательно, данное сочетание оказывается невозможным.

Сочетание ААО противоречит правилу 6-му, потому что заключение отрицательно, в то время как посылки утвердительны.

Если таким способом исследовать все 64 случая, то останется только 11 сочетаний, которые дают правильные силлогизмы. Эти сочетания след.: ААА, ААI, АЕЕ, АЕО, AII, AOO, EAE, ЕАО, ЕIО, IАI, ОАО.

Мы поставили своей задачей решение вопроса, сочетание каких суждений может давать правильные силлогизмы. Казалось бы, что указанным способом мы разрешаем тот вопрос, который нас интересует, но в действительности это не так, потому что при составлении этих сочетаний нужно принять в соображение еще положение среднего термина в посылках. В том силлогизме, который мы до сих пор рассматривали, средний термин в большей посылке является подлежащим, а в меньшей посылке сказуемым. Но среднему термину мы можем придавать произволь-

84

 

 

ное положение: мы можем средний термин сделать сказуемым в обеих посылках или подлежащим в обеих посылках, или, наконец, сказуемым в большей посылке и подлежащим в меньшей. Сообразно с этим мы получаем так наз. четыре фигуры силлогизма, которые и изображены на прилагаемой схеме.

 

Эта схема дает возможность помнить положение среднего термина. Горизонтальные линии соединяют посылки, а наклонные и вертикальные линии соединяют средний термин в обеих посылках. Если обратить внимание на то, что наклонные и вертикальные линии, соединяющие средний термин, расположены симметрично, то легко помнить положение среднего термина.

Фигуры и модусы силлогизма. В первой фигуре средний термин является подлежащим в большей посылке, сказуемым в меньшей. Во второй фигуре он является сказуемым в большей посылке, сказуемым же в меньшей посылке. В третьей фигуре он является подлежащим и в большей, и в меньшей посылке, и, наконец, в четвертой фигуре он является сказуемым в большей посылке и подлежащим в меньшей.

Теперь мы возьмем те 11 возможных сочетаний и предположим, что каждое сочетание изменяет положение среднего термина указанными четырьмя способами, тогда получится 44 сочетания.

Нам опять предстоит рассмотреть, какие из них возможны. Чтобы показать, как производится такого рода исследование, возьмем для примера сочетание АЕЕ, изобразим его по первой фигуре.

А Все М суть Р

Е Ни одно S не есть М__

Е Ни одно S не есть Р.

Если мы обратим внимание на термин Р, то окажется, что в большей посылке, как сказуемое обще-утвердительного суждения, он не распределен, между тем как в заключении, как сказуемое обще-отрицательного суждения, он

85

 

 

распределен. Это противоречит четвертому правилу, а следовательно, такое сочетание невозможно. Рассмотрим далее, какой вид может принять это сочетание по второй фигуре:

А Все Р суть М

Е Ни одно S не есть М___

Е Ни одно S не есть Р.

Здесь нет нарушения правил силлогизма, а потому заключение правильно. Но если это заключение мы рассмотрим по третьей фигуре, то заключение будет нарушать 4-е правило. Именно силлогизм примет такой вид:

А Все М суть Р

Е Ни одно М не есть S

Е Ни одно S не есть Р.

По четвертой фигуре это сочетание будет правильно.

Если мы указанным только что способом исследуем все 44 сочетания, то получим следующих 19 правильных видов силлогизма или модусов, распределенных по фигурам:

Всякий изучающий логику должен все эти модусы знать наизусть. Для облегчения же заучивания придумали следующее стихотворение, написанное гекзаметром:

Здесь каждое слово, напечатанное курсивным шрифтом, означает отдельный модус, посылки и заключение которого легко определить, если^; изъять гласные буквы. Напр., Barbara означает модус первой фигуры, в котором обе посылки и заключение суть ААА, Gelarent означает модус ЕАЕ. Значение остальных букв этих слов будет изложено в следующем примечании.

86

 

 

* Если бы учащийся сам захотел по указанному выше способу определить, какие сочетания суждений дают правильные силлогизмы, то он может воспользоваться след. указаниями.

Если он, руководясь правилами гл. 14-й, станет отбрасывать те сочетания, которые противоречат правилам, то у него должно остаться след. 12 сочетаний: AAА AAJ АЕЕ АЕО AJJ AOO EAE ЕАО EJO JAJ ОАО JEO. Из них последнее сочетание JEO следует также отбросить, потому что оно противоречит четвертому правилу, именно в заключении больший термин берется во всем объеме, как сказуемое отрицательного суждения, в то время как в большей посылке, как сказуемое или как подлежащее частно-утвердительного суждения, он взят не во всем объеме. Таким образом остается всего 11 сочетаний.

Если затем он проведет остающиеся 11 сочетаний до четырем фигурам, то у него, кроме тех 19 сочетаний, которые приведены выше, останутся еще 5 сочетаний, именно по 1-й фигуре AAJ и ЕАО, по 2-й фигуре ЕАО и АЕО и по 4 й фиг. АЕО. Хотя эти 5 сочетаний дают правильное заключение, но их все-таки следует отбросить, потому что они дают ослабленное или подчиненное заключение, именно они дают частное заключение, в то время как могут давать и общее. В самом деле, возьмем сочетание AAJ по первой фигуре:

Все научные сведения полезны.

Химические сведения научны

Некоторые химич. сведения полезны

Хотя это заключение правильно, но при данных посылках можно получить и общее заключение: „все химические сведения полезны“. Поэтому данное сочетание следует считать практически бесполезным.

Таким образом, если мы отбросим эти 5 сочетаний, дающих ослабленные заключения, то у нас останутся те 19 сочетаний, которые приведены выше.

Возьмем для иллюстрации фигур и модусов примеры. Фигура 1-я.

Barbara

А Все хищные животные питаются мясом

А Тигры суть хищные животные

А Тигры питаются мясом.

Этот силлогизм символически можно изобразить следующим образом. «Хищные животные», как средний термин обозначим при помощи М; «питающиеся мясом», как больший термин, посредством Р, а «тигры» посредством S; тогда силлогизм изобразится при помощи схемы на рис. 23.

Gelarent

Е Ни одно насекомое не имеет более трех

пар ножек

А Пчелы суть насекомые______________

Е Пчелы не имеют более трех пар ножек.

87

 

 

Схема этого модуса изображена на рис. 24.

 

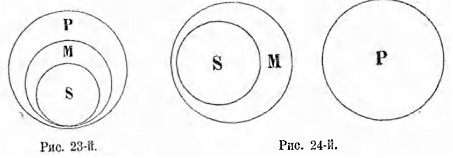
Darií

А Все хищные животные питаются мясом

I Некоторые домашние животные суть хищные животные

I Некоторые домашние животные питаются мясом.

(См. рис. 25-й).

                Ferio

Е Ни один невменяемый не наказуем

I Некоторые преступники невменяемы  

О Некоторые преступники не наказуемы.

(См. рис. 26-й).

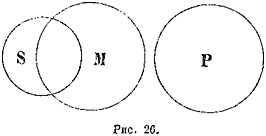
Cesare

Е Ни один справедливый человек не завистлив

А Всякий честолюбивый завистлив

Е Ни один честолюбивый человек не есть справедлив.

(См. рис. 27.)                                 

 

88

 

 

Camestres

A Преступник действует из злого намерения

ЕN не действовал из злого намерения

ЕN не есть преступник.

Festino

Е Ни один благоразумный человек не суеверен

I Некоторые хорошо образованные люди суеверны

О Некот. хорошо образован. люди неблагоразумны.

Baroko

А Все истинно моральные действия совершаются

из правильных мотивов

О Некоторые действия, благодетельные для других, не совершаются из таких мотивов

О Некоторые благодетельные для других действия не суть истинно моральные.

Фигура 3-я.

Darapti

А Все киты суть млекопитающие

А Все киты живут в воде

I Некоторые живущие в воде животные суть млекопитающие.

Данное умозаключение относится к третьей фигуре, где средний термин в обеих посылках является подлежащим. Меньший термин «живущие в воде существа» взят в меньшей посылке не во всем объеме; следовательно, и в заключении должен быть взят не во всем объеме (см. рис. 28).

Felapton

Е Ни один глухонемой не может говорить

А Глухонемые суть духовно-нормальные люди

О Некоторые духовно-нормальные люди не могут говорить

(Схему см. на рис. 29.)

 

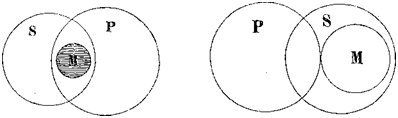
рис. 28   рис. 29 

89

 

 

Disamis

IНекоторые романы поучительны

А Все романы суть вымышленные рассказы

I Некот. вымышленные рассказы поучительны.

Ferison

Е Ни одна наступательная война не может быть оправдана

IНекот. наступательные войны были успешны

O Некоторые успешные войны не могут быть оправданы.

Фигура 4-я. Возьмем силлогизм:

Bramantip

А Все металлы суть материальные вещи

А Все материальные вещи имеют тяжесть

I Некотор. тела, имеющие тяжесть, суть металлы.

В этом силлогизме средний термин взят сказуемым в большей и подлежащим в меньшей посылке. Сказуемое в меньшей посылке взято не во всем объеме, потому и в заключении оно должно быть взято не во всем объеме. Таким образом получается заключение: «некоторые тела, имеющие тяжесть, суть металлы». Эта фигура называется Галеновской от имени Галена (200 после Р. Хр.); ее не было у Аристотеля.

Еще пример для иллюстрации четвертой фигуры.

Camenes

А Все квадраты суть параллелограммы

Е Ни один параллелограмм не есть треугольник

Е Ни один треугольник не есть квадрат.

Характеристика фигур. Характеризуем в общих чертах все четыре фигуры силлогизма в отношении их познавательного значения.

1-я фигура. В ней меньшая посылка утвердительная, а большая общая(sit minor affirmans, nec major sit specialis). Эта фигура упохребляехся в тех случаях, когда нужно показать применение общих положений (аксиом, основоположений, законов природы, правовых норм и т. п.) к частным случаям; это есть фигура подчинения.        

90

 

 

2-я      фигура. В этой фигуре одна из посылок должая быть отрицательною и большая посылка должна быть общею(una negans esto, nec major sit spe­cialis). Посредством этой фигуры отвергаются ложные дедукции или ложные подчинения. Например, кто-нибудь утверждает относительно испытуемого газа, что он есть кислород. Нам стоит указать на какой-нибудь признак, который не присущ испытуемому газу, для того чтобы убедиться в том, что это не есть кислород. Тогда у нас получится следующий силлогизм:

А Кислород поддерживает горение

Е Этот газ не поддерживает горения

Е Этот газ не есть кислород.

Кто-нибудь утверждает, что данное лицо больно лихорадкой; утверждая это, он производит подчинение. Нам нужно отвергнуть это подчинение. Тогда ми составляем следующий силлогизм:

А Все больные лихорадкой испытывают жажду

Е Этот больной не испытывает жажды

Е Этот больной ие болен лихорадкой.

Таким образом по второй фигуре отвергаются ложные подчинения и именно потому, что одна из посылок отрицательна. Юридические приговоры строятся по этой фигуре. Например:

А Этот смертельный удар нанесен человеком, обладающим огромной силой

Е Обвиняемый не есть человек, обладающий огромной силой___________________________________________

Е Обвиняемый не нанес смертельного удара.

3-я      фигура. В третьей фигуре меньшая посылка должна быть утвердительной, а заключение должно быть частным(sit minor afiirmans, conclusio sit specialis). Поэтому в третьей фигуре обыкновенно отвергается мнимая общность утвердительных и отрицательных суждений или доказывается исключение из общего положения. Положим, нам нужно доказать, что утверждение «все металлы тверды» допускает исключение, что оно не всеобще. Тогда мы строим силлогизм по третьей фигуре:

91

 

 

Е Ртуть не тверда

А Ртуть есть металл

О Некоторые металлы не тверды.

4-я фигура имеет искусственный характер и обыкновенно не употребляется.

Характер посылок и заключений каждой фигуры может быть наглядно представлен, если мы буквы модусов каждой фигуры расположим по вертикальным линиям таким образом, что буквы больших посылок будут идти по горизонтальной, буквы меньших посылок по второй горизонтальной и буквы заключений по третьей горизонтальной.

Вопросы для повторения. Чем обусловливается различие между фигурами силлогизма? Какие существуют фигуры силлогизма и какое различие между ними? Перечислите модусы всех четырех фигур. Какое различие между фигурами в отношении познания?

 

ГЛАВА 16-я.

* Сведение фигур силлогизма.

Мы видели, что существуют различные фигуры и модусы силлогизмов. Спрашивается, равноценны ли они? все ли равно, если мы будем умозаключать по первой, второй или третьей фигуре? Оказывается, нет, и именно предпочтение следует отдать модусам первой фигуры. Доказательства по этой фигуре имеют особенно очевидный характер.

Для проверки истинности силлогистического вывода, выраженного при помощи какого-либо модуса той или иной фигуры, следует этот модус свести к какому-либо модусу первой фигуры, и именно потому, что очевидность заключения

92

 

 

по первой фигуре можно доказать, показавши применимость аксиомы силлогизма к модусам первой фигуры. В символических обозначениях модусов, которые мы привели в предыдущей главе, есть указание на то, каким образом должно происходить это сведение к модусам 1-й фиг.

Буква s показывает, что суждение, обозначенное предшествующею ему гласною, должно подвергнуться чистому обращению (coversio simplex).

Буква р показывает, что суждение, обозначенное предшествующею ему гласной, нужно обращать per accidens или посредством ограничения.

Буква m показывает, что посылки силлогизма нужно переместить, т.-е. большую посылку нужно сделать меньшей в новом силлогизме, а меньшую большей (нужно произвести metathesis или mutatio praemissarum).

В, С, D, F,начальные согласные названий, показывают модусы первой фигуры, получающиеся от сведения. Так, Cesare, Camestres и Camenes второй и четвертой фигуры можно свести к Celarent первой фигуры; Darapti, Disamis третьей фигуры можно свести к Darii, Fresison к Ferio.

k показывает, что данный модус может быть доказан через посредство какого-либо модуса первой фигуры при помощи особого приема, который называется reductio per deduc­tionem ad impossibile, или короче reductio ad impossibile. Этот прием сведеяия называется таише reductio ad absurdum.

Разсмотрим несколько примеров сведений.

Модус Cesare второй фигуры, как показывает начальная буква, сводится к модусу Gelarentпервой фигуры. Буква s в обозначении этой фигуры показывает, что в суждении Е должно произвести простое обращение. Сведение Cesareк Celarentможно сделать ясным при помощи сопоставления схем этих модусов.

Cesareсводится к Celarent

Из сопоставления схем видно, что произошло только чистое обращение в большей посылке.

Модус Daraptiсводится к Dariiпервой фигуры и именно

93

 

 

следующим образом. Меньшую посылку нужно обратить посредством ограничения, т.-е. из суждения «все М суть S» должно получиться суждение: «некоторые S суть М».

Daraptiсводится к Darii

Пример.

Bramantip сводится к Barbara путем перестановки посылок:

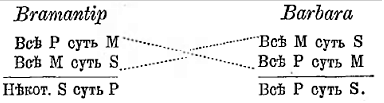
После того как сделано заключение, в нем необходимо сделать обращение, па что указывает буква р; тогда получится: «Некоторые S суть Р».

Пример.

Рассмотрим еще сведение Camestresк Celarent.Для осуществления такого сведения необходимо произвести перестановку посылок, обративши меньшую посылку чисто, а равным образом сделавши чистое обращение в заключении.

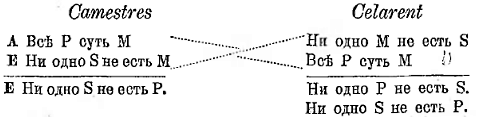
94

 

 

Reductio adabsurdum. Наконец, рассмотрим еще один способ сведения, это именно сведение посредством reductio ad absurdum = приведение к нелепости; он применяется, как уже было сказано, во всех тех модусах, в которых есть буква k.

К таким модусам относятся Baroko и Bokardo. Буква В в начале обозначения показывает, что для сведения необходимо воспользоваться модусом Barbara. Этот способ называется reductio adabsurdum (сведение к нелепости) по следующей причине. Мы, имея две посылки, приходим к известному выводу. Кто-нибудь утверждает, что наш вывод неверен. Тогда наша задача заключается в том, чтобы показать нелепость его утверждения. Для этого мы стараемся показать, что нельзя, признавая данные посылки, не признавать нашего заключения или вывода.

Возьмем умозаключение по модусу Baroko:

А Все Р суть М

О Некоторые S не суть М

О След., некоторые S не суть Р.

Будем отрицать справедливость заключения: «Некоторые Sне суть Р». Если мы не признаем истинным заключение, то мы должны признать истинность противоречащего ему суждения. Поэтому, если ложно, что «некоторые S не суть Р», то должно быть истинным, что «все S суть Р». Поэтому примем, что «все S суть Р». Сделавши принятое положение меньшей посылкой, как это показывает буква k*), мы получаем следующий силлогизм по Barbara с Р в качестве среднего термина:

Все Р суть М

Все S суть Р

Все S суть М.

*) Именно k показывает, что посылка, обозначение которой предшествует букве к, должна быть замещена положением, противоречащим заключению.

95

 

 

Итак, если отрицать первоначальное заключение, то мы должны будем прийти к заключению, что «все S суть М». Но это заключение находится в противоречии с меньшей посылкой, которая была принята за истинную. Таким образом ясно, что тот, кто нам возражал, пришел к противоречию, принимая наши посылки, но не принимая нашего заключения. Это значит, что мы показали нелепость его возражения, мы привели его возражение adabsurdum.

Рассмотрим еще пример сведения Bokardo при помощи применения reductio ad absurdum. Схема Bokardo.

Некот. М не суть Р

Все М суть S

Некот. S не суть Р.

Отрицая истинность заключения: «некоторые Sне суть Р», мы должны признать истинность суждения, противоречащего ему, именно: «все S суть Р». Соединяя эту посылку с посылкой «все М суть S», принятой нами за истинное, мы получим силлогизм Barbara с S в качестве среднего термина:

Все S суть Р

Все М суть S

Все М суть Р.

Таким образом в заключении у нас получается, что «все М суть Р», а это противоречит посылке «некоторые М не суть Р», принятой за истинное. «Все М суть Р» не может быть истинным, если мы уже ранее допустили, что «некоторые М не суть Р».

Рассмотрим на примере сведение Bokardo.

О Некоторые искусства не суть подражание природе.

А Все искусства представляют прекрасное.

О Некоторые прекрасные вещи не есть подражание природе.

Если мы станем думать, что заключение этого силлогизма ложно, то истинным должно быть противоречащее ему суждение, именно: «все прекрасное есть подражание природе». Поставим это суждение на место большей посылки и соединим с меньшей посылкой, тогда получится след. силлогизм Barbara:

Все прекрасное есть подражание природе.

Все искусства изображают прекрасное.

Все искусства суть подражание природе.

96

 

 

Но это заключение находится в противоречии с допущенным нами положением. Такого рода противоречие получилось вследствие того, что мы допустили положение, противоречащее нашему заключению. Если мы пришли к нелепости, благодаря этому последнему допущению, то очевидно, что мы не можем делать его и что наше первоначальное заключение правильно.

Мы рассмотрели таким образом, как сводятся различные модусы второй, третьей и четвертой фигур к модусам первой фигуры. Но для чего нужно такое сведение? Ответ на этот вопрос будет следующий. Так как на первой фигуре особенно ясно можно видеть применимость аксиомы силлогизма dictum de omni, то очевидно, что при помощи сведения к первой фигуре становится ясным также правильность и модусов остальных фигур, потому что раз при помощи аксиомы силлогизма мы убеждаемся в очевидности модусов первой фигуры, то мы убеждаемся также и в очевидности других фигур, которые равнозначны модусам первой фигуры.

Вопросы для повторения. Что такое сведение силлогизмов? Что обозначают буквы s, р, m, k в обозначении силлогизмов? Что такое reductio ad absurdum? Покажите применение этого способа на сведении Bokardo и Baroko. Для чего нужно сведение?

 

ГЛАВА 17-я.

Условные, разделительные и условно-разделительные силлогизмы.

Условные или гипотетические силлогизмы. До сих пор мы рассматривали силлогизм, в котором посылками служат категорические суждения, но мы видели, что, кроме категорических суждений, есть еще условные и разделительные суждения. Поэтому могут быть такие силлогизмы, в посылки которых входят суждения условные или разделительные или и те и другие.

Как мы видели, схема условного суждения будет такова:

Если А есть В, то С есть D.

Первое суждение, как мы видели, называется «основанием», второе называется «следствием». Можно составить такой сил-

97

 

 

логизм, в котором одна из посылок будет условным суждением; тогда у нас получится условный силлогизм»

Есть два типа условных силлогизмов:

Модус ponens или конструктивный.

Если А есть В, то С есть D

_____А есть В__________

След., С есть D

Пример:

Если дождь идет, то почва мокрая

Дождь идет

След., почва мокрая.

Этот тип умозаключения называется modus ponens, потому что в нем основание полагается, утверждается (от ponere ставить); в нем в меньшей посылке содержится утверждение основания. Вследствие того, что утверждается основание, утверждается также и следствие, потому что в данном случае основание есть причина следствия.

Второй тип условных силлогизмов называется:

2) Модус tollens или деструктивный. Он называется modus tollens потому, что меньшая посылка содержит отрицание, и именно следствия(tollere = уничтожать).

Если А есть В, то С есть D

_____С не есть D________

След., А не есть В.

Пример:

Если дождь идет, то почва мокрая

Но почва не мокрая

След., дождь не идет.

В этом силлогизме в меньшей посылке отрицается следствие, вследствие этого в заключении отрицается основание.

Таким образом получаем два типа условного силлогизма. Первый называется также модус конструктивный, потому что в нем получается утвердительное заключение (от construo = строю, созидаю), второй тип называется модус деструктивный, потому что в нем получается отрицательное заключение (от destruo = разрушаю).

Следует заметить, что в условных силлогизмах можно умозаключать только лишь от утверждения основания к утверждению следствия и от отрицания следствия к отрицанию основания, но нельзя умозаключать от утверждения следствия к утверждению основания и от отрицания основания к отрицанию

98

 

 

следствия. Это оттого, что одно и то же действие может созидаться различными причинами. В самом деле, если я отрицаю, что данная причина произвела то или другое действие, то из этого не следует, что его не могла произвести какая-нибудь другая причина; если я утверждаю, что данное действие произошло, то это не значит, что оно порождено данной причиной, потому что могло быть множество других причин, которые могли его породить.

Для пояснения этого возьмем следующий условный силлогизм:

Если кто-нибудь читает хорошие книги, то он приобретает познания.

NN приобрел познания.

Мы здесь утверждаем следствие. Можем ли мы утверждать основание? Следует ли отсюда, что NN читал хорошие книги? Нет, так как он эти познания мог приобрести при помощи различных других способов, например, при помощи общения с учеными людьми, слушания лекций и т. п. Приобретение познаний имеет своей причиной не одно только чтение хороших книг, но и многие другие причины.

Попробуем отрицать основание, возьмем тот же силлогизм.

Если кто-нибудь читает хорошие книги, то он приобретает познания.

NN не читает хороших книг.

Следует ли отсюда, что он не приобретет познания? Нет, не следует до тем же соображениям, которые только что были приведены.

Разделительные силлогизмы называются так потому, что в одну из посылок их (именно в большую) входит разделительное суждение. Как мы видели, общая форма разделительного суждения будет:

А есть или В, или С, или D, или Е.

Каждый член разделительного суждения называется альтернативой.

Существует следующих два типа разделительного силлогизма:

1) Modus ponendo tollens. В этом силлогизме в меньшей посылке утверждается один из членов деления боль-

99

 

 

шей посылки, или одна альтернатива; в заключении же вследствие этого все остальные члены отрицаются.

Его форма:

А есть или В, или С, или D, или Е.

А есть В.

След., А не есть ни С, ни D, ни Е.

Пример:

Треугольники бывают или остроугольные, или тупоугольные или прямоугольные.

Данный треугольник есть остроугольный.

След., он не есть ни прямоугольный, ни тупоугольный.

Для правильности этого вида умозаключения необходима правильность большей, посылки, т.-е. необходимо, чтобы члены деления были перечислены сполна и чтобы они исключали друг друга.

2) Modus tollendo ponens. В этой форме, в противоположность предыдущей, в меньшей посылке отрицаются все члены деления, за исключением одного, который и утверждается в заключении.

Его схема:

А есть или В, или С, или D.

А не есть ни В, ни С.

След., А есть D.

Пример:

Треугольники бывают или остроугольные, или тупоугольные, или прямоугольные.

Данный треугольник не есть ни остроугольный, ни тупоугольный.

След., он не есть прямоугольный.

Этот вид разделительных умозаключений употребляется в геометрии под именем непрямого доказательства. Напр.:

Известная сумма должна быть или больше, или меньше, или равна тому-то.

Но она ни больше, ни меньше.

След., она равна.

Условие правильности разделительного силлогизма, как это легко видеть, сводится к правильности разделительных суждений, входящих в качестве посылки в состав разделительного силлогизма.

Условно-разделительные силлогизмы. Наконец, последняя группа умозаключений— это условно-разделитель-

100

 

 

ные или лемматические. Это такие умозаключения, в которых бóльшая посылка состоит из двух или больше условных суждений, а меньшая состоит из разделительного.

Здесь мы различаем следующие четыре формы умозаключений:

1) Простой модус ponens или конструктивный. Он называется ponens потому, что меньшая посылка утвердительная: конструктивным он называется потому, что заключение утвердительное. Его схема:

Если А есть В, то С есть D; если Е есть F, то C ест D.

Но или А есть В, или Е есть F.

След., С есть D.

Пример:

Если кому-нибудь суждено выздороветь, то лекарство бесполезно.

Если кому-нибудь не суждено выздороветь, то лекарство бесполезно.

Но человеку, может быть суждено или выздороветь или не выздороветь.

След., и в том и в другом случае лекарство бесполезно.

Заметим, что в этой форме умозаключения в меньшей посылке утверждаются основания.

От этого простого модуса сложный отличается тем, что в нем в условных суждениях нет одного общего основания или общего следствия, как это мы имеем в простом модусе, и самое заключение выражается при помощи разделительного суждения.

2) Сложный модус ponens или конструктивный. Его схема:

Если А есть В, то С есть D; и если Е есть F, то G есть Н.

Но или А есть В, или Е есть F.

След., или С есть D, или G есть Н.

Пример:

Если я брошусь из окна, то я получу ушибы.

Если я пойду по лестнице, то я сгорю.

Но я должен или броситься из окна, пли пойти по лестнице.

След., я или ушибусь или сгорю.

Заметим, что в этой форме умозаключения в меньшей посылке также утверждается основание.

3) Простой модус tollens или деструктивный:

Если А есть В, то С есть D; и если А есть В, то Е есть F.

Ho С не есть D и Е не есть F.

След., А не есть В.

101

 

 

Пример:

Если бы мы захотели начать войну, то мы должны были бы или сделать заем, или увеличить налоги.

Мы не можем сделать ни того, ни другого.

След., мы не можем предпринять войны.

В этой форме силлогизма в меньшей посылке отрицаются следствия, а потому отрицаются и основания.

4) Сложный модус tollens или деструктивный:

Если А есть В, то С есть D; и если Е есть F, то G есть Н.

Ho С не есть D и G не есть Н.

След., А не есть В и Е не есть F.

Пример:

Лицо, желающее иметь автомобиль, может так рассуждать:

Если бы я был богат, то я автомобиль купил бы,

Если бы я был бесчестен, то я украл бы таковой.

Но я не куплю и не украду.

След., я не богат и не бесчестен.

Лемматические умозаключения по количеству следствий называются дилеммой, трилеммой и т. д. *).

Достоверность лемматического умозаключения находится в зависимости от правильности условных суждений в большей посылке и от полноты членов деления в меньшей. Так как эти условия часто не соблюдаются, то лемматическое умозаключение делается источником ошибок.

Источником ошибок является чаще всего неполное перечисление членов деления. Двумя альтернативами иногда нельзя исчерпать всего возможного числа случаев. Весьма часто дилемматическое умозаключение строят таким образом, что из всех возможных альтернатив берут только две альтернативы, вследствие чего и получается ошибка.

Пример:

Если какой-либо ученик любит учиться, то он не нуждается ни в каком поощрении. Если же он чувствует отвращение к учению, то всякое поощрение окажется бесполезным.

*) Альтернативы лемматического умозаключения назывались в средние века „рогами“ силлогизма; сам силлогизм назывался syllogismus cornutus. Это название получилось от употребления дилеммы в спорах. Как легко видеть, особенность дилемматического умозаключения состоит в том, что какую бы альтернативу мы ни избрали, мы приходим к одному и тому же неприятному заключению. Противник может избрать какую угодно альтернативу он все равно поймается, «очутится в рогах дилеммы».

102

 

 

Но ученик может или любить учение, или чувствовать к нему отвращение.

След., поощрение или излишне, или бесполезно в деле обучения.

Эта дилемма ложна, потому что «любовь к учению» и «отвращение к учению» не суть единственно возможные альтернативы, так как могут быть такие ученики, которые не питают любви к учению, но не питают и отвращения к нему; для таких учеников поощрение в виде награды может быть действительным.

Вопросы для повторения. Какие силлогизмы называются условными и какие типы условных силлогизмов мы различаем? Какие силлогизмы мы называем разделительными и какие типы их мы различаем? От чего зависит достоверность разделительных силлогизмов? Что называется альтернативой? Какие силлогизмы называются условно-разделительными? Какие четыре типа их мы различаем и чем они отличаются друг от друга? Что такое дилемма, трилемма? От чего зависит достоверность лемматического умозаключения?

 

ГЛАВА 18-я.

Сокращенные и сложные силлогизмы.

Сокращенные силлогизмы. Перейдем к рассмотрению тех силлогизмов, которые называются сокращенными и сложными силлогизмами; они по форме отличаются от обыкновенных. Некоторые утверждали, что мы в мышлении никогда не пользуемся силлогизмами. Но это неправильно, потому что в обиходной жизни мы пользуемся весьма часто силлогизмом, но только он не всегда бывает выражен полно, и именно оттого, что некоторые части его бывают выпущены. Эти силлогизмы называются сокращенными или также энтимемами. Это название происходит от слова ἐνθύμημα. Энтимема—это такой силлогизм, часть которого мы держим в уме (ἐνθυμῷ), а часть выражаем. Мы можем выбрасывать каждую часть силлогизма и мыслить все-таки силлогистически. Напр., если мы относительно кого-нибудь употребим выражение: «нужно быть дурным человеком, чтобы делать подобные вещи», то это выражение представляет собою силлогизм, который, если мы ему придадим полную форму, приобретет след. вид:

Все люди, которые делают подобные вещи, дурны

Этот человек делает подобные вещи

След., он дурной человек.

103

 

 

Для того, чтобы пояснить, как происходит этот пропуск частей силлогизма, возьмем какой-нибудь полный силлогизм, напр.:

Всякий порок заслуживает порицания

Скупость есть порок

След., скупость заслуживает порицания.

Этим примером можно воспользоваться для того, чтобы иллюстрировать след. три вида энтимемы:

1-й    вид:

Скупость заслуживает порицания, потому что она есть порок. (Здесь пропущена большая посылка.)

2-й    вид:

Скупость заслуживает порицания, потому что всякий порок заслуживает порицания. (Здесь пропущена меньшая посылка.)

3-й    вид;

Всякий порок заслуживает порицания, скупость же есть порок... (Здесь пропущено заключение и именно потому, что оно очевидно.)

Эпихейрема. Есть, наконец, еще один вид сокращенных силлогизмов, который называется эпихейремой. Это такой силлогизм, в обе из посылок которого входят энтимемы. Схема эпихейремы:

М есть Р, так как оно есть N.

S есть М, так как оно есть 0.

След., S есть Р.

Первая посылка должна была бы быть так выражена:

Все N суть Р.

Все М суть N.

След., М есть Р.

Вторая посылка должна была бы быть выражена так:

Все О суть М.

Все S суть О.

След., все S суть М.

Пример:

Ложь заслуживает презрения, так как она безнравственна.

Лесть есть ложь, так как она есть умышленное извращение истины.

След., лесть должна быть презираема.

104

 

В этом силлогизме, как это легко видеть, каждая из посылок есть суждение, которое представляет собою заключение со средним термином; если же дать заключение со средним термином, то этого вполне достаточно для того, чтобы восстановить весь силлогизм.

Теперь рассмотрим те силлогизмы, которые называются сложными.

Полисиллогизмы. Может случиться, и собственно в научной мысли весьма часто бывает, что мы несколько силлогизмов соединяем в один, и тогда получается то, что называется цепью силлогизмов—полисиллогизмом.

Соединение силлогизмов происходит таким образом, что заключение одного силлогизма является посылкой для другого. Тот силлогизм, который предшествует, называется просиллогизмом; тот силлогизм, который следует после, называется эписиллогизмом.

Схема полисиллогизма будет следующая:

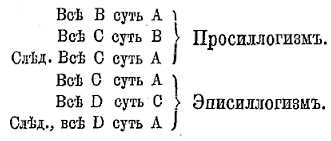
Есть два типа просиллогизмов, В первом умозаключение идет от более общего к менее общему, во втором, наоборот, умозаключение идет от менее общего к более общему. Первый тип называется прогрессивным, второй—регрессивным.

Пример прогрессивного полисиллогизма.

Все позвоночные имеют красную кровь

Все млекопитающие суть позвоночные

Все млекопитающие имеют красную кровь.

Все млекопитающие имеют красную кровь

Все хищные суть млекопитающие

Все хищные имеют красную кровь.

Все хищные имеют красную кровь

Тигры суть хищные животные

Тигры имеют красную кровь.

Здесь умозаключение идет от более общего к менее общему (позвоночные, млекопитающие, хищные, тигры), т.-е.

105

 

 

шествует вперед по отношению к содержанию, так как в частных понятиях содержание больше.

Пример регрессивного полисиллогизма.

Позвоночные суть животные

Тигры суть позвоночные

Тигры суть животные.

Животные суть организмы

Тигры суть животные

Тигры суть организмы.

Организмы разрушаются

Тигры суть организмы

Тигры разрушаются.

Здесь умозаключение идет от менее общего к более общему (позвоночное, животное, организм, разрушимое).

* Сориты. Иногда при соединении нескольких силлогизмов для плавности мысли мы можем пропускать некоторые посылки. В таком случае получается то, что называется соритом. Существует два вида соритов: 1) Аристотелевский, когда выбрасывается меньшая посылка каждого отдельного силлогизма, и 2) Гоклениевский, когда выбрасывается большая посылка отдельных силлогизмов.

Возьмем примеры:

1) Аристотелевский сорит.

Буцефал есть лошадь

Лошадь есть четвероногое

Четвероногое есть животное

Животное есть субстанция

Буцефал есть субстанция.

Если бы этому сориту мы придали полную форму, т.-е. восстановили бы опущенные посылки, то у нас получилось бы следующих три силлогизма:

1) Лошадь есть четвероногое

Буцефал есть лошадь

Буцефал есть четвероногое.

2) Четвероногое есть животное

[Буцефал есть четвероногое]

Буцефал есть животное.

3) Животное есть субстанция

[Буцефал есть животное]

Буцефал есть субстанция.

2) Гоклениевский сорит:

Животное есть субстанция

Четвероногое есть животное

106

 

 

Лошадь есть четвероногое

Буцефал есть лошадь

Буцефал есть субстанция.

Это есть Гоклениевский сорит, потому что выпущены большие посылки.

Если бы мы восстановили пропущенные посылки, то у нас получился бы следующий ряд силлогизмов:

1) Животное есть субстанция

Четвероногое есть животное

Четвероногое есть субстанция.

2) [Четвероногое есть субстанция]

Лошадь есть четвероногое

Лошадь есть субстанция.

3) [Лошадь есть субстанция]

Буцефал есть лошадь

Буцефал есть субстанция.

Вопросы для повторения. Что такое энтимема и сколько типов энтимем мы различаем? Что такое эпихейрема? Что такое полисиллогизм? Что такое просиллогизм и эписиллогизм? Какое различие между просиллогизмом прогрессивным и регрессивным? Что такое сорит? Какое различие между соритом аристотелевским и гоклениевским?

 

ГЛАВА 19-я.

*Силлогизм и его значение.

Мы рассмотрели различные формы силлогизма и его применение; но спрашивается, какое он имеет познавательное значение? Этот вопрос следует поставить потому, что относительно познавательного значения силлогизма высказывались два противоположных взгляда.

Аристотель считал силлогизм орудием достоверного познания, т.-е., по Аристотелю, только то познание следует считать истинно-научным познанием, которое можно облечь в силлогистическую форму. Такой взгляд Аристотеля обусловливался тем, что, по его мнению, понятия находятся в вещах или воплощаются в единичных вещах. Силлогизм же является орудием достоверного познания потому, что процесс силлогизации приводит к соединению понятий. Сущность наших научных построений заключается в том, чтобы отыскать среднее понятие, т.-е. то понятие, благодаря которому осуществляется процесс силлогизации. Результатом

107

 

 

силлогизации является известная связь понятий, которая показывает связь реальных вещей потому, что отношение между понятиями в нашем уме соответствует отношениям между понятиями, существующими реально. Следовательно, из формального в нашем уме мы можем познавать реальное в природе. Вот почему раскрытие этой связи понятий имело такую большую цену в глазах Аристотеля и его последователей в древности и в средние века. Они думали, что силлогизм есть главное орудие для открытия научных истин, для развития науки. Поэтому в средневековой науке и философии силлогизм и играл такую важную роль.

Бэкон. Но такое значение силлогизма подверг сомнению английский философ Бэкон, который находил, что силлогизм не может быть орудием научного познания по следующим причинам. Силлогизм состоит из суждений; суждения состоят из понятий, которые являются результатом обобщения. Следовательно, понятие есть то,  на чем основывается силлогизм. Если понятия составляются не точно, то и силлогизм будет не точен. Поэтому в научном познании самым главным является процесс образования понятий. Вследствие этого не силлогизм есть главное орудие познания, а индукция, при помощи которой получаются понятия. Индукция таким образом является главным средством научного познания.

Д. С. Милль. Но самые сильные возражения против силлогизма были представлены Д. С. Миллем. Он находил, что в силлогизме существенный недостаток заключается в том, что он не дает ничего нового. Силлогизм поставляет целью доказать заключение, признав за истинное большую посылку. Но имеет ли он право делать это последнее? Нет, потому, что достоверность большей посылки уже предполагает достоверность заключения, т. е. мы не имеем права признать достоверности большей посылки, если мы не признаем достоверности заключения. В самом деле, когда мы строим силлогизм:

Все люди смертны

Сократ человек

След., Сократ смертен,

то наше заключение «Сократ смертен» уже предполагается в суждении: «Все люди смерены». Мы не можем утверждать,

108

 

 

что «все люди смертны», до тех пор, пока мы не убедились, что каждый человек в отдельности смертен, а в том числе и Сократ. Следовательно, если мы в большей посылке утверждаем, что все люди смертны, то это потому, что мы уверены, что и Сократ смертен. Если же это так, то спрашивается, что же мы доказываем при помощи силлогизма? Очевидно, что при помощи силлогизма мы можем получить в заключении только то суждение, которое уже предполагается большей посылкой. Следовательно, силлогизм доказывает только то, что уже заранее известно. Силлогизм сам по себе ничего не доказывает, потому что из большей посылки мы можем вывести не всякие частные случаи, а только те, которые и большей посылкой принимаются за известные. В таком случае, по-видимому, силлогизм никакого научного значения не имеет, потому что он не дает ничего нового. Заключение содержит только то, что уже есть в посылках.

Но, с другой стороны, по мнению Милля, несомненным является то обстоятельство, что в некоторых случаях мы при помощи силлогизма получаем новые истины. Например, «мы убеждены, что герцог Веллингтон, который еще не умер, смертен». Но мы не знаем этого из прямого наблюдения, так как он еще не умер. Если бы кто-нибудь спросил нас, почему мы знаем, что герцог Веллингтон смертен, то мы, вероятно, ответили бы: потому что все люди таковы. Следовательно, мы приходим здесь к познанию истины, (пока) недоступной наблюдению, посредством умозаключения, которое может быть представлено в следующем силлогизме:

Все люди смертны

Герцог Веллингтон человек

След. герцог Веллингтон смертен.

Если же путем силлогизации мы можем получать новые истины, то как это обстоятельство можно примирить с вышеприведенным утверждением Милля, что в процессе силлогизации мы в заключении не получаем ничего больше того, что содержится в большей посылке?

По мнению Милля, выход из этого противоречия заключается в следующем. Обыкновенно неправильно выражаются, когда говорят, что в силлогизме заключение получается из

109

 

 

общего предложения, как если бы заключение содержалось в большей посылке; заключение получается не из общего предложения, а только лишь согласно общему предложению. Чтобы это понять, надо заметить, что, по Миллю, не существует вывода от общего к частному. Дедуктивное умозаключение есть только видимость. В действительности существует только индуктивное умозаключение, которое является в двух формах, или 1) как заключение от частного к общему, которое и называется собственно индукцией, или 2) как заключение от частных к частным. Мы можем заключать от частных к частным или прямо, или не прямо, через посредство общего предложения. Этот второй случай и представляет собою дедукцию. Таким образом, умозаключение от частных к частным, но через посредство общего составляет дедукцию.

Чтобы сделать этот взгляд вероятным, Милль старается показать, что вообще в процессе познания мы весьма часто прибегаем к умозаключению от частного к частному «Мы не только,говорит он, можем умозаключать от частных кчастным, не обращаясь к общему, но и беспрестанно так умозаключаем. Дитя, которое, обжегши палец, избегает совать его снова в огонь, сделало умозаключение или вывод, хотя оно отнюдь не имело в мысли общего предложения: «огонь жжет». «Я убежден, говорит Милль, что в действительности, заключая от своих личных опытов, а не из правил, сообщаемых нам книгами или преданием, мы заключаем от частных кчастным чаще прямо, чем через посредство Какого-нибудь общего предложения». Если мы, напр., переводим что-либо на иностранный язык,то мы можем воспользоваться тем или иным правилом, т.-е. чем-либо общим, но мы чаще переводим, умозаключая от частного к частному, без посредства общего правила, на основании применения какого-либо частного примера. Таким образом, даже научно-образованные люди не всегда обращаются е общим предложениям.

[Так как дедукция, по определению Милля, есть умозаключением от частного к частному через посредство общего, то какова же роль общего предложения в процессе силлогизации? На этот вопрос Милль отвечает следующим образом. Когда мы составляем какое-нибудь общее предложе-

110

 

 

ние, то, мы, как это легко понять, только в краткой форме суммарно, выражаем множество наблюденных нами фактов. Но в тот самый момент, когда мы производим обобщение, мы сознаем, что мы приобретаем право прилагать его к частным случаям. Когда мы из наблюдения смертности Ивана, Петра, Фомы, т.-е. наблюдения частных случаев, высказали общее суждение «все люди смертны», то, произнося это общее суждение, мы как бы говорим себе, что это обобщение мы имеем право прилагать ко всем  людям. Когда мы теперь при помощи приведенного выше силлогизма приходим к выводу о смертности Сократа, то это есть вывод от наблюденных нами частных случаев к частному, но через посредство общего предложения «все люди смертны». Таким образом, когда мы строим силлогизм, то мы только истолковываем наше общее предложение, которое мы тогда составили. Мы как бы спрашиваем себя, на какие выводы мы уполномочивали себя в то время, когда мы производили обобщение «все люди смертны».

Так объясняет Милль то обстоятельство, что дедукция, получающая свое выражение в силлогизме, в сущности есть умозаключение от частного к частному, но только через посредство общего предложения, при чем посредство этого общего предложения совсем не имеет важного значения для большей достоверности.]

Таким образом Милль приводит два возражения против силлогизма: 1) силлогизм не содержит ничего нового: он сводится только к раскрытию того, что уже содержится в наших общих предложениях; 2) силлогистический процесс есть на самом деле умозаключение от частного к частному.

Недостатки теории Милля, Что дедукция, т.-е. умозаключение от общего к частному, имеет весьма важное значение, что без общего предложения нельзя было бы умозаключать, что вставка общего предложения имеет весьма существенное значение,—можно объяснить следующим образом. Когда мы, обобщая на основании наблюдения смертности только некоторых людей, произносим суждение: «все люди смертны», то в этом процессе обобщения мы выходим далеко за пределы того, что мы наблюдаем. В нашем утверждении заключается убеждение, что оно справедливо по отношению ко

111

 

 

всем людям, где бы и когда бы они ни существовали. Свойство смертности нам представляется необходимым свойством человека; где бы и когда бы мы ни встретили существо, которое обладает такой природой, что мы его можем назвать человеком, то такому существу мы припишем свойство смертности. В процессе силлогизации мы применяем общее положение к частному случаю, и это именно является весьма существенным для силлогизма. Существенной составной частью силлогизма является меньшая посылка, которая показывает, что данный частный случай именно подходит под общее положение. Если мы умозаключаем, что, например, президент Соединенных Штатов умрет, то только на том основании, что мы при помощи меньшей посылки удостоверяем, что он человек, а из этого следует, что его необходимым свойством должна быть смертность.

Таким образом ясно, что сущность силлогизма заключается не в том, что он повторяет в заключении то, что уже было в большей посылке, а в том, что данный индивидуальный случай подводится под общее положение, а именно, что президент Соединенных Штатов — человек. Из этого ясно также, что в заключении силлогизма всегда получается нечто новое, потому что, когда мы произносим большую посылку, то мы вовсе не имеем в виду и тот индивидуум или и те частные случаи, о которых говорится в меньшей посылке.

Если мы примем в соображение, что для возможности умозаключения необходимо, чтобы в большей посылке содержалось именно общее положение, указывающее на то, что смертность необходимо связана с природой человека, то для нас сделается ясным, что без этого мы не можем утверждать смертности того или другого человека. Отсюда ясна несостоятельность взгляда Милля, по которому дедукции собственно нет, что существует только умозаключение от частного к частному, а также и несостоятельность того положения, что силлогизм не дает ничего нового.

Вопросы для повторения. Изложите взгляд Аристотеля на значение силлогизма. Изложите взгляд Бэкона. Какие два возражения против силлогизма приводил Милль? Какие недостатки в теории Милля?

112

 

ГЛАВА 20-я.

Об индукции.

В прошлой главе мы окончили рассмотрение того вида умозаключения, который называется дедукцией и который представляет собою умозаключение от общего к частному. В настоящей главе мы рассмотрим тот вид умозаключения, который называется индукцией или наведением. Различие между этими двумя видами умозаключения сводится к следующему.

В дедуктивном умозаключении при признании какого-либо общего суждения мы необходимо должны признать какое-либо частное суждение или менее общее суждение; в индуктивном умозаключении мы от признания ряда частных суждений переходим к признанию общего суждения.

Определение индукции. Ближе индукцию можно определить следующим образом: индукция есть умственный процесс, посредством которого мы выводим, что истинное в каком-либо частном случае или частных случаях будет истинным и во всех случаях, сходных с предыдущими. Напр., я заметил, что в нескольких случаях растения произрастали лучше от притока влаги; из этих наблюдений я делаю заключение, что это будет справедливо по отношению ко всем случаям произрастания известного класса растений. Если я наблюдаю, что какие-либо тяжелые тела при погружении в воду теряют часть своего веса, равную весу вытесненной ими жидкости, то я делаю заключение, что это будет справедливо относительно всех тел и относительно всех жидкостей.

Таким образом в процессе индуктивного умозаключения мы умозаключаем от случаев, которые мы наблюдали и исследовали, к случаям, которых ныне наблюдали и не исследовали. Далее, вследствие того, что в процессе индукции мы от наблюдения части класса умозаключаем ко всему классу, индукция есть умозаключение от частного к общему или умозаключение от менее общего к более общему.

Не все однако считают это индукцией; некоторые философы думают, что индукцией следует называть такое умозаключение от частного к общему, в котором заключение относится ко всем исследованным случаям. Это та индукция, которая называется полной или совершенной.

113

 

 

Полная и неполная индукция. Полной индукцией называется тот вид индукции, в заключении которого говорится только о тех случаях, о которых говорится также и в посылках. Если я, рассмотрев месяцы года, нахожу, что ни один из них не имеет больше 31 дня, и высказываю это в виде общего положения, то это будет полной индукцией. Если я, исследовавши национальность каждого ученика, сидящего в классе, и узнавши, что каждый из них есть француз, выражаю в виде общего положения: «все ученики класса суть французы», то это будет полной индукцией. По мнению некоторых, это есть единственная индукция, заслуживающая название индукции, потому что она имеет безусловно достоверный характер. Но если применять то определение индукции, которое было предложено выше, то для нас сделается ясным, что такого рода заключения не могут быть названы индукцией, потому что индукция в собственном смысле есть умозаключение от известного к неизвестному. В индуктивном умозаключении в выводе всегда должно получаться что-нибудь новое, между тем как в полной индукции ничего нового не получается, потому что заключение в полной индукции есть только повторение в краткой форме того, что содержится в посылках: это есть простое резюмирование посылок. Индуктивным умозаключением является именно неполная индукция, в которой мы из исследования только некоторых случаев умозаключаем к классу случаев; исследовав только часть класса, умозаключаем ко всему классу.

Популярная индукция. Существуют индуктивные построения, которые не могут удовлетворять требованиям научной точности. Это—построения, которыми склонно пользоваться популярное сознание и которое поэтому называется популярной индукцией.

В чем заключается популярная индукция?

Если мы имеем случай наблюдать многократное повторение сходных явлений, то мы стремимся думать, что эти явления всегда будут иметь место, если только мы не имели случая наблюдать явлений, противоречащих им. Если мы, например, много раз во многих местах имели случай наблюдать, что лебеди имеют белый цвет перьев, то мы делаем заключение, что лебеди всегда и везде имеют белый цвет перьев. Такое заключение Бэкон на-

114

 

 

звал: inductio per enumerationem simplicem, ubi nonreperitur instantia contradictoria (индукция через простое перечисление, в котором не встречается противоречащего случая), потому что в ней делается вывод на основании простого перечисления, пересмотра сходных случаев, которые были у нас в прошлом опыте и которым не было противоречащего случая. Кажется, что чем больше случаев наблюдаемой связи, тем большую достоверность приобретает выводимое заключение. Такая индукция присуща уму неразвитому. Она не может быть признаваема достоверной, потому что то обстоятельство, что мы не встречали случаев, противоречащих тем, которые мы наблюдали, отнюдь не является ручательством, что всегда будет так, как мы наблюдали.

От популярной индукции отличается индукция научная. В этом процессе исследуют каждый отдельный наблюдаемый случай, анализируют его, все случайное для данного явления отбрасывают, ищут существенные признаки его и строят заключения, приводя в связь и согласие эти последние с другими обобщениями. Такие выводы только и могут иметь характер более или менее достоверный. Это можно пояснить при помощи только что приведенного примера. Если мы на основании наблюденных нами лебедей делаем заключение, что «все лебеди белы», то такая индукция будет популярной, потому что на основании тщательных исследований относительно цвета перьев птиц мы должны прийти к заключению, что цвет представляет из себя нечто непостоянное, не связанное необходимо с природой лебедя, а потому легко может случиться, что окажутся лебеди, обладающие черным цветом перьев.

Индукция должна иметь дело с необходимой связью вещей, а не со случайной. Связь между белым цветом перьев и организацией лебедя не является необходимой; черный цвет перьев лебедя не есть что-либо такое, что противоречит другим обобщениям. Цвет перьев для птиц не есть что-либо существенное, т.-е. не есть что-либо такое, от чего могла бы зависеть жизнь или существо птиц. Совсем иное дело, если бы мы, произведя наблюдение над процессом дыхания у лебедей, сказали, что «лебеди дышат кислородом». Это было бы правильной научной индукцией, потому что способность вдыхания кислорода есть такое свойство, без которого птицы не мыслимы. Точно таким же образом мы

115

 

 

поступаем во всех тех случаях, когда нам вообще приходится строить индуктивные положения относительно наблюдаемых нами явлений.

Понятие законов природы. Пользуясь индуктивным умозаключением, мы можем открывать законы природы.

Но что же такое законы природы?

Это—предложения, которые выражают постоянное свойство или постоянную связь каких-нибудь явлений. Например, положение, что «жидкость в сообщающихся сосудах находится на одном и том же уровне», есть закон природы. «Животные вдыхают кислород» — закон природы.

Первою существенною чертою закона природы следует признать его всеобщность: описание какого-нибудь единичного факта, хотя бы оно было совершенно верно, не может быть названо законом. Закон всегда служит для выражения свойств, общих ряду явлений или классу явлений.

Другая существенная черта в понятии закона—это необходимость. Положение: «тело, лишенное опоры, будет падать», есть закон, потому что действительно тело, лишенное опоры, необходимо будет падать. «Железо теплопроводно»—закон природы, потому что в железе теплота будет необходимо распространяться, т.-е. если теплота будет приведена в соприкосновение с железом, то это последнее необходимо будет проводить ее. Если бы оказалось, что изучаемая связь один раз имеется налицо, а в другой раз не имеется, то мы то предложение, которое служит для выражения этой связи, не могли бы назвать законом. Вот почему научные обобщения, считающиеся законами, сейчас же перестают быть ими, как только найден хоть один случай, в котором они не применяются.

Основание индукции. Мы при помощи индукции исследуем природу, составляя общие положения. Но на чем мы основываемся, когда мы составляем такие общие положения? Что дает нам право обобщать или на что мы опираемся, когда по одному факту или по ряду сходных фактов заключаем о классе сходных с ними фактов? что дает нам право делать выводы от наблюденных случаев к не наблюденным? Например, исследовавши сжимаемость одного или двух газов, мы, обобщая, утверждаем, что «все

116

 

 

газы сжимаемы». Для того чтобы мы имели право делать вывод от того, что мы наблюдали, к тому, чего мы не наблюдали, мы должны исходить из предположения, что вещи обладают постоянными свойствами, т.-е. вещи устроены так, что сегодня известные причины вызывают те же действия, что и вчера, завтра известные причины будут вызывать те же действия, что и сегодня. Если соприкосновение железа с кислородом сегодня производит в нем ржавчину, то у нас есть уверенность, что так будет всегда, потому что железо и кислород обладают такими свойствами, что взаимодействие их всегда будет производить ржавчину. Таким образом у нас есть убеждение, что вещи обладают постоянными свойствами и поэтому во всех случаях действуют однообразно. Это можно еще иначе выразить, если сказать, что в природе существует однообразный порядок. У нас есть убеждение в однообразном порядке природы. Только благодаря тому, что у нас есть такое убеждение, мы можем умозаключать от вещей наблюденных к вещам ненаблюденным. Такое убеждение мы называем убеждением в однообразии природы, или убеждением в том, что существует закон однообразия природы. Закон однообразия природы обыкновенно формулируется так: «природа однообразна», «будущее похоже на настоящее».

Индуктивное умозаключение, таким образом, опирается на закон однообразия природы или на положение, что будущее похоже на настоящее. Если на минуту предположить, что нет однообразия в вещах природы, то индуктивное умозаключение тотчас же теряет смысл. Если мы не уверены в том, что; будущее похоже на настоящее, то мы не имеем права умозаключать от того, что мы наблюдали, к тому, чего еще не было, чего мы еще не наблюдали.

Но это положение необходимо доказать, потому что на доказательстве его основывается доказательность каждого индуктивного умозаключения. Но как мы можем его доказать? Как мы можем доказать, что будущее похоже на настоящее, что вещи не изменяют своих свойств? Ведь будущего еще не было, а потому мы совсем не знаем, так ли это? Мы можем сослаться на то, что до сих пор так всегда было; до сих пор природа, по-видимому, не изменяла

117

 

 

своего однообразного хода, мы до, сих пор всегда имели случай убеждаться в том, что вещи не изменяли своих свойств. Отсюда мы можем сделать предположение, что и на будущее время вещи не изменят своих свойств. Но это не есть доказательство. Это есть inductio per enume­rationem simplicem, которую мы осудили, как ненаучную индукцию.

Следует признать, что закон однообразия природы не может быть доказан. Такие положения, которые не могут быть доказаны, но которые тем не менее являются основой научного познания, называются постулатами.

Вопросы для повторения. Как определяется индукция? Чем отличается индукция от дедукции? Что такое полная и неполная индукция? Что такое популярная индукция, и чем она отличается от научной? На чем основан вывод в популярной индукции? Что такое законы природы и каковы их характерные особенности? На каком законе основывается индукция? Что такое постулаты?

 

ГЛАВА 21-я.

Методы индуктивного исследования.

Определение причинности. В прошлой главе мы видели, что при помощи индуктивного умозаключения мы можем открыть законы природы; при помощи индуктивного умозаключения мы можем познать также и причинную связь вещей. Но что такое причина? Под причиною следует понимать явление, которое так связано с другим явлением, называющимся действием, что его возникновение неизбежно влечет за собою возникновение действия, и уничтожение его неизбежно влечет за собою уничтожение действия. Внешним признаком причины является то, что она нам представляется явлением предшествующим, а признаком действия то, что оно представляется последующим. Причинное отношение или причинную связь мы должны признать там, где известное явление неизбежно, неизменно следует за другим. Напр., появление огня неизменно влечет за собою появление теплоты.

Когда мы исследуем природу, то мы можем видеть, что явления природы представляют истинный хаос: явления находятся друг с другом в беспорядочной смеси. Для познания причинной связи мы должны различить, какие из сме-

118

 

 

няющих друг друга явлений предшествующие и какие из них последующие. Когда мы это сделаем, то нашей ближайшей задачей явится исследование того, каким образом эти предшествующие и последующие соединены между собою; присущ ли этой связи явлений тот признак, который был указан выше, потому что только определенная связь предшествующих и последующих может быть признана нами причинной связью явлений. Для определения причинной связи нам необходимо встретить как некоторые предшествующие, так и некоторые последующие разъединенными. Именно, первоначально мы должны умственно выделить предшествующие от последующих, а затем, если возможно, то произвести и реальное разделение их. Только при этом условии мы будем в состоянии усмотреть, изменения какого предшествующего влекут за собою изменения последующего и какие из изменяющихся явлений поэтому мы должны признать причиной и какие действием.

Опыт и наблюдение. Для разъединения предшествующих от последующих нам иногда необходимо изменять обстоятельства, при которых совершается изучаемое явление: мы сами должны вмешаться в ход явлений и видоизменять этот последний. Такого рода вмешательство в ход явлений называется опытом, или экспериментом. Если мы, изучая свойство какого-либо явления, не производим произвольно никаких изменений, то такой способ познания будет называться наблюдением. Наблюдение есть изучение событий и вещей в том виде, в каком они даны в природе.

Различие между наблюдением и экспериментом сводится к следующему.

В процессе наблюдения мы изучаем явления в том виде, в каком они нам даны в природе. При помощи наблюдения просто мы изучаем свойства такой болезни, как холера, так как мы не можем произвести ее искусственно. В эксперименте же мы изменяем  те обстоятельства, при которых совершаются изучаемые нами явления. В эксперименте мы изменяем по нашему произволу комбинации вещей и обстоятельства и затем наблюдаем результат. Так, химик, пользуясь электрическим током, разъединяет две составных части воды—кислород и водород. Благодаря опыту мы мо-

119

 

 

жем произвести то видоизменение явлений, в котором мы нуждаемся для определения причинной связи их.

Легко видеть те преимущества, которые представляет эксперимент в сравнении с наблюдением просто.

Прежде всего эксперимент способствует умножению числа изучаемых явлений. Если мы изучаем какое-либо явление только при помощи наблюдения, то мы должны выжидать, когда в природе произойдет интересующее нас явление, напр., снег, электрические явления и т. п. При помощи эксперимента мы можем, искусственно воспроизводя известное явление, повторять его и, благодаря этому, обращать внимание на те стороны явления, которые ускользают при простом наблюдении.

При помощи эксперимента мы можем изолировать изучаемое явление, отделить его от всего того, что для нашей цели неважно, и, благодаря этому, мы можем получить точный случай того явления, которое мы изучаем.

Кроме того, при помощи эксперимента мы можем также выделять предшествующие от последующих и, благодаря этому, определить причинную связь между ними, именно при помощи эксперимента мы можем выделить те обстоятельства, которые несущественны для возникновения изучаемого явления.

Для определения причинной связи существуют четыре способа или метода исследования, которые у Д. С. Милля носят следующие названия: 1) метод согласия, 2) метод разницы, 3) метод остатков и 4) метод сопутствующих изменений. Благодаря этим методам, мы можем определить, как связаны между собою предшествующие и последующие.

Метод согласия. Рассмотрим сначала пример, для того, чтобы вывести правило этого метода. Предположим, что я в кухне вижу, что если в печку положить уголья и они разгораются, то вода, которая находится в котле, начинает кипеть и образуется пар. Положим, после этого я иду в поле я вижу, что вода в котле, под которым развели костер, тоже кипит и тоже образуется пар. Наконец, я иду в лабораторию химика и вижу, что вода в сосуде, под которым находится спиртовая лампочка, кипит и тоже образуется пар. Я ставлю вопрос, какова причина образования

120

 

 

пара? Чтобы ответить на этот вопрос, я умственно выделяю предшествующие события от последующих и в числе первых ищу причину данного явления. Я мог бы подумать, что причиной парообразования является наличность угля в печке, но этому противоречит то обстоятельство, что во втором и в третьем из наблюденных мною случаев парообразования не было угля. Следовательно, уголь не может быть причиной парообразования, если оно могло происходить и в его отсутствии. В таком случае, может быть, причиной парообразования является присутствие дров; но и это предположение неверно, потому что дров не было в первом и в третьем случае. Нельзя также сказать, что причиной парообразования является спирт, потому что его не было в первом и втором случае. Чтобы ответить на интересующий нас вопрос, мы должны искать в числе предшествующих такой элемент, который являлся бы общим  для всех случаев; это и будет настоящей искомой причиной парообразования. Таким общим является огонь, который находится в числе всех наблюденных мною случаев и который поэтому мы должны считать причиной парообразования. Это есть определение причинности по методу согласия.

Таким образом, когда мы определяем причинную связь по методу, называемому методом согласия или сходства, то мы сравниваем между собою различные случаи, в которых изучаемое явление имеет место, выделяя в них часты предшествующие и последующие. Обозначим предшествующие буквами A В С D Е, а последующие буквами а b с dе, и пусть а будет тем действием, причину которого нам нужно определить. Предположим, что мы исследовали А в соединении с В и С и что действие их было а bс; далее предположим, что мы исследовали А в соединении с D и Е, но, без В и С, и что действие их было ade. Тогда ни В, ни С, ни D, ни Е не могут быть причинами а, тогда как в первом случае а возникает без D и Е, а во втором случае без В и С. Поэтому причиной а может быть только А.

Способ определения причинности по первому методу может быть формулирован следующим образом: „если двум или большему числу случаев исследуемого явления природы обще лишь одно обстоятельство, то именно то обстоятельство, в котором все случаи согласуется, есть причина данного явления».

121

 

 

Этот метод можно символизовать при помощи следующей схемы:

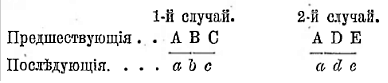
Метод разницы. По второму методу исследование причинной связи явлений производится следующим образом. Положим, нам дается ряд предшествующих А В С и ряд последующих аb с. Требуется определить, что является причиной а. Для этого мы в ряду предшествующих отбрасываем один член, например, А, тогда в ряду последующих отпадает член а. Если удаление А влечет за собою удаление а, то это является знаком того, что А есть причина а. Таким образом по этому методу мы сравниваем случай, в котором исследуемое явление имеется налицо, со случаем, в котором исследуемое явление не имеется налицо. Этот метод называется методом разницы, и правило его формулируется следующим образом:

„Если случай, в котором известное явление природы наступает, и случай, в котором оно не наступает, имеют общими все обстоятельства за исключением лишь одного, и это одно обстоятельство встречается только в первом случае, то обстоятельство, в котором оба случая разнятся между собою, есть причина или необходимая часть причины изучаемого явления природы“.

Напр., мы знаем, что легкие тела: перья, пух, вата, падают не с тою скоростью, с какою падают другие тела. Мы можем поставить вопрос, какова причина неодинаковой скорости падения. Для разрешения этого вопроса мы в ряду обстоятельств, при которых совершается падение тел, устраняем воздух, именно мы производим падение тел в стеклянном сосуде, из которого предварительно выкачали воздух. Тогда мы видим, что и указанные тела падают с тою скоростью, с какою падают и другие тела. Если устранение воздуха повлекло за собою устранение неравенства скорости падения, то это значит, что воздух или сопротивление воздуха есть причина неравенства скорости падения.

Схема метода разницы будет следующая:

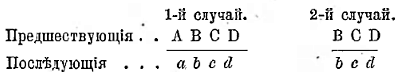
122

 

 

Соединение метода сходства с методом разницы называется соединенным  методом. Его можно пояснить при помощи следующего примера. Я заметил, что какое-нибудь растение находится постоянно в изобилии на какой-нибудь почве, но в то же время я нахожу, что оно не растет ни на какой другой почве. Отсюда я делаю заключение, что причиной произрастания данного растения является именно почва (т.-е. какие-нибудь химические составные части этой почвы).

Метод остатков. Сущность этого метода сводится к следующему. Нам дан ряд явлений А В С, которые мы считаем предшествующими, и затем дан ряд явлений а b с, которые мы считаем последующими. Пусть из предыдущего опыта нам известно, что А есть причина а, а В есть причина b; тогда, вычтя эти известные нам причины, мы получим, что С есть причина с. При помощи этого метода была открыта новая планета Нептун. Именно оказалось, что наблюдаемые движения Урана не находились в согласии с движениями, найденными посредством вычисления. Движение Урана то замедлялось, то ускорялось. Надо было определить причину нарушения движения Урана. Было известно, какое количество нарушения в движениях Урана было обязано влиянию известных в то время небесных светил. Когда произвели вычитание этого известного уже воздействия, то в остатке получалось нарушение, причину которого нужно было найти. Нужно было предположить существование еще какой-то неизвестной планеты, принимающей участие в определении пути Урана. Такой планетой оказался Нептун.

Правило метода остатков следующее:

„Вычти из данного явления природы ту часть его, которая, благодаря прежним индукциям, известна, как действие определенных предшествующих, и остающаяся часть (остаток) явления природы будет действием остальных предшествующих".

Метод сопутствующих изменений. Но бывают случаи, когда ни один из методов, приведенных выше, не оказывается' пригодным для исследования причинной связи явлений. Это бывает именно тогда, когда известное явление по самой своей природе не может быть отделено или изолировано от другого явления. Например, «состояние теплоты» и «объем тел» не могут быть отделены друг ои друга: теплоту нельзя выделить из тела так, чтобы она существо-

123

 

 

вала отдельно от тел. Поэтому если нам нужно, например, изучить причинную связь между теплотой и объемом тел, то на первый взгляд кажется, что изучение этой связи невозможно. Но в действительности, если мы не можем изолировать или исключить такое явление, то мы можем произвести какое-либо изменение в нем и затем видеть, вызывает ли это изменение какое-либо изменение в том явлении, которое с ним связано. Например, мы можем теплоту увеличивать или уменьшать, и в то же время видеть, что происходит с объемом. Если с увеличением теплоты увеличивается объем тела и с уменьшением теплоты уменьшается объем, то мы заключаем, что теплота есть причина увеличения объема.

„Если некоторое изменение предшествующего А всегда сопровождается переменою в последующем a, а другие последующие bи с остаются теми же, или наоборот, если каждой перемене а предшествовало видоизменение в А, которое не было замечаемо в других предшествующих, то мы можем заключать, что а вполне или отчасти есть действие А или же, по крайней мере, соединено с ним некоторой связью причины с действием“.

Для иллюстрации применения этого метода рассмотрим вопрос, какое влияние оказывает луна на поверхность земли. Мы не можем произвести опыт в отсутствии луны, т.-е. мы не можем устранить луну, мы не можем наблюдать, какие явления уничтожаются на земле вместе с уничтожением луны или какие явления возникают в то время, когда появляется луна. Но мы можем наблюдать, какие возникают явления на земле в то время, как луна изменяет свое положение по отношению к земле. Именно мы находим, что все изменения в положении луны сопровождаются соответственными изменениями в высоте воды в океане, при чем местом изменения всегда бывает или часть земли, самая близкая к луне, или самая далекая от нее; отсюда мы убеждаемся, что луна вполне или отчасти есть причина приливов и отливов.

Метод сопутствующих изменений применяется в определении причинности в явлениях общественной жизни. Когда мы, напр., находим, что количество преступлений уменьшается вместе с распространением народного образования, то мы предполагаем, что эти явления находятся в причинной связи друг с другом.

124

 

 

Вопросы для повторения. Как определяется причина? Что такое эксперимент? Какое различие между экспериментом и наблюдением? Какие преимущества эксперимента перед наблюдением? Какие существуют четыре метода исследования причинности? Как формулируется метод согласия? Его правило и схема. Как формулируется метод разницы? Его правило и схема. Как формулируется метод остатков? Его правило. Как формулируется метод сопутствующих изменений? Когда применяется метод сопутствующих изменений?

 

ГЛАВА 22-я.

Роль дедукции,

Для открытия законов природы необходимо пользоваться индуктивными методами исследования, как это мы видели в прошлой главе. Но открытию законов способствует не только индукция, а равным образом и дедукция.

Дедуктивный метод исследования может употребляться в науках в двух случаях. Во-первых, он употребляется как средство объяснения закона, уже открытого индуктивно, именно когда найденный закон можно свести к одному или нескольким законам более общего характера, которые поэтому можно назвать высшими законами. Во-вторых, дедуктивный метод употребляется как средство открытия законов, которые невозможно открыть индуктивно, но которые возможно дедуктивно вывести из законов уже известных.

Дедуктивное объяснение законов. Рассмотрим предварительно роль дедукции в объяснении законов.

Но что значит в этом случае термин объяснение, что значит объяснить закон? В этом случае понятие объяснения употребляется в том же самом смысле, в каком оно употребляется, когда дело идет об объяснении факта. Мы считаем известный факт объясненным в том случае, если его можно вывести из какого-нибудь общего закона, Например, человек умер вследствие введения какого-то вещества в желудок. Мы спрашиваем, почему произошла смерть; как объясняется данный факт (т.-е. смерть человека)? Данный факт будет объяснен, если, констатируя, что вещество, введенное в желудок, имеет все признаки мышьяка, мы можем вывести этот факт из общего положения

125

 

 

«мышьяк есть яд». Процесс дедукции, применяемый нами в данном случае, вполне очевиден.

Подобно тому как факты могут быть объясняемы дедуктивно, так могут быть объясняемы и законы. Мы отмечаем следующее различие между законами. Поскольку закон, найденный индуктивно, не может посредством дедукции выводиться из какого-либо другого более общего или высшего закона, он называется эмпирическим законом. (Это, как мы видели, есть индукция через простое перечисление.) Например, из многочисленных наблюдений над влиянием хины на организм был сделан индуктивный вывод, что «хина излечивает лихорадку»; это есть индуктивный закон, но в то же время это есть эмпирический закон, потому что не объясняется, почему хина излечивает лихорадку. Если мы дадим ответ на последний вопрос, то мы объясним эмпирический закон; тогда эмпирический закон перестанет быть эмпирическим и сделается производным. Объяснение эмпирического закона состоит в сведении его на более общий закон. Таких объяснений эмпирических законов в науках о природе Милль различает три вида.

Первый вид. Мы иногда открываем законы какого-нибудь явления при помощи индукции и затем приходим к убеждению, что этот закон выводится из других законов. Так, например, Кеплер открыл закон, что «планеты движутся по эллипсу», но объяснить, отчего это так, он не был в состоянии. Ньютон показал, что этот закон может быть объяснен двумя более общими законами, именно законом центробежной силы, стремящейся двигать планету по касательной к ее орбите, и законом тяготения, которое стремится бросить планету на солнце *). Легко ви-

*) Что движение планеты, напр., луны, находится под влиянием двух сил, можно пояснить при помощи чертежа 30, „где Е представляет землю, а МВА—орбиту луны. Предположим, что луна находится в М. Если бы притяжение земли перестало действовать на нее, то луна продолжала бы двигаться по той же прямой линии, по которой она двигалась в тот самый момент, как притяжение перестало действовать на нее, и она пошла бы по направлению к N и в течение одной секунды дошла бы, положим, до М'. Но мы находим, что вследствие притяжения земли луна на самом деле находится в В, и это показывает, что притяжение земли притянуло луну от М' до В“ (Локайер. Уроки элементарной астрономии).

126

 

 

деть, что оба эти закона имеют более общий характер, чем закон движения планет.

Второй вид. Мы часто открываем причинную связь между явлениями А и Б; нам кажется, что А и Б связаны друг с другом непосредственно. Между тем впоследствии мы убеждаемся в том, что между указанными двумя членами есть промежуточный член или несколько таковых. Например, между А и С, на которые мы смотрели, как на причину и действие, есть промежуточный член В, так что отношение между А и С оказывается не одним законом причинности, а цепью таких законов, в которой А есть причина В и только В есть причина С. Например, прикосновение сахара к языку вызывает ощущение сладкого вкуса. Поэтому можно сказать, что сахар есть причина ощущения сладкого вкуса. Но между прикосновением сахара к языку и возникновением сладкого вкуса есть целый ряд звеньев. Сахар поглощается слизистою оболочкою языка и приходит в соприкосновение в волокнами вкусовых нервов; из этого возникает химический процесс в нерве, который, распространяясь по нерву в форме молекулярного движения, доходит до головного мозга, результатом возбуждения которого является то состояние, которое называется ощущением сладкого вкуса. Таким образом, между прикосновением сахара к языку и ощущением сладкого вкуса вставляется целый ряд процессов. Общие положения, которые служат для выражения этих промежуточных процессов, и служат для объяснения закона причинной связи между А и С.

Может казаться, что этот второй вид объяснения не содержит в себе никакой дедукции, никакого подведения под другой более общий закон. На самом же деле такое подведение действительно существует, потому что законы промежуточных процессов общее первоначального положения. В самом деле, если мы говорим, что сахар поглощается слизистою оболочкою языка, то потому, что мы здесь предполагаем общее положение, что слизистые оболочки вообще обладают способностью поглощать различные вещества. Далее, если мы говорим, что во вкусовом нерве происходит химический процесс, который распространяется по нерву в форме молекулярного движения, то мы этот процесс рассматриваем, как частный случай молекулярного движе-

127

 

 

ния в случае возникновения химического процесса. Наконец, когда мы говорим, что возбуждение мозга вызывает ощущение сладкого вкуса, то это есть частный случай более общего процесса, когда возбуждение мозга вызывает те или иные психические процессы.

Таким образом, объяснение в этом случае заключается в том, что между двумя данными членами причинной связи вставляются промежуточные процессы, которые могут быть объяснены законами более общего характера.

Третий вид. Наконец, третий вид объяснения законов состоит в соединении нескольких законов в один закон, обнимающий их. Этот вид объяснения представляет простой процесс обобщения. Например, мы называем известный процесс горением. Но если мы между горением и покрытием железа ржавчиной усматриваем нечто общее, именно, что горение и покрытие ржавчиной представляют собою процессы соединения с кислородом, то мы подводим их под высшее понятие; их объединяющее, именно «окисление». Это более общее понятие и служит объяснением для менее общих понятий.

Значение объяснения законов. Таким образом, рассмотревши три вида объяснения законов, мы видим, что объяснение какого-нибудь закона заключается в сведении его к законам более общим. Это объяснение законов, или превращение эмпирических законов в производные, имеет громадное научное значение.

Наука делает каждый раз шаг вперед, когда эмпирический закон делается производным посредством дедукции, потому что объяснение эмпирического закона точно определяет сферу приложения его. Эмпирические законы не должны быть прилагаемы за пределами времени, места и вообще обстоятельств, при которых они найдены, т,-е. если мы нашли какой-нибудь закон при тех или иных обстоятельствах времени и места, то мы, не имеем права утверждать, что он будет действителен и при других обстоятельствах времени и места, потому что мы вообще не знаем, в каких пределах он может быть приложим. Если же эмпирический закон сделается производным,то он тогда точно указывает, в каких пределах он может быть приложим. Чтобы показать, как важно

128

 

 

превращение эмпирических законов в производные, возьмем пример.

Эмпирическим путем было найдено, что вода в насосе не может подняться выше 33 футов. Это был факт, но факт не объясненный. Вследствие этого нельзя было сказать, так ли это происходит на других планетах, так ли это происходит на высоких горах и т. п. Но вот закон из эмпирического сделался производным, потому что было найдено, что поднятие воды в насосе обусловливается давлением атмосферы. Эмпирический закон был объяснен. Как только это произошло, тотчас можно было определить точные границы приложимости этого эмпирического закона. Мы теперь знаем, где этот закон не будет иметь применения. Мы знаем, что на вершинах высоких гор высота поднятия воды в насосе должна быть ниже 33 футов, что другие жидкости, как, например, алкоголь, серная кислота и т. п., не поднимутся до этой высоты. Ни одно из этих ограничений не могло бы быть получено эмпирическим путем. Превращение эмпирического закона в производный дало тотчас же все эти ограничения.

Дедуктивное открытие законов. Дедуктивное открытие законов бывает тогда, когда действие одной причины смешивается с действием другой (напр., на какое-либо тело действуют две силы под углом; требуется определить путь, который совершит данное тело). В этом случае необходимо бывает определить, какое может получиться действие от комбинации данных причин.

В применении этого метода можно отличать три момента.

Первый момент — это нахождение простейших законов отдельных причин при помощи индукции. Именно при помощи индукции определяются законы отдельных причин, которые, входя в соединение друг с другом, производят известное действие.

Второй момент составляет силлогизация, т.-е. выведение из уже известных законов отдельных причин того сочетания их действий, какое нужно для того, чтобы создать исследуемое сложное явление. Дедукция в собственном смысле состоит в определении по законам отдельных причин, каково будет действие, производимое сочетанием этих причин.

129

 

 

Третью часть составляет проверка вычисления или вывода посредством сравнения результатов вычисления с наблюдением над изучаемым сложным явлением. Это есть сопоставление действия предсказанного и действия данного.

Для того, чтобы пояснить применение дедуктивного метода для открытия законов природы, возьмем в пример задачу: определить, какой путь совершит ядро при полете его из дула пушки.

При помощи дедуктивных исследований мы знаем упругость газов, развивающихся в дуле пушки; индуктивным же путем мы знаем, как велико сопротивление воздуха, и равным образом, какое влияние оказывает земное притяжение.

Имея эти данные, мы пользуемся уже дедуктивным методом для решения нашей задачи. При помощи силлогизации мы определяем, как должно быть велико сопротивление для данного случая (для этого нам необходимы общее положение и данный частный случай). Путем силлогизации мы определяем, какова будет линия полета, если бы действовала только одна упругость газов. Приняв в соображение эти и другие данные, мы определяем линию полета.

Затем нам необходимо еще произвести проверку. Для этого мы выпускаем ядро из орудия и таким путем проверяем, было ли правильно наше умозаключение.

Таким образом при помощи силлогизации мы в состоянии определить, какое действие будет следовать за данным сочетанием причин.

Из изложенного ясно, что дедукция имеет очень важное значение для раскрытия законов природы. Поэтому де следует думать, как это делают некоторые, что только индукция служит для открытия законов природы.

Из изложенного в этой главе легко видеть, что именно соединение дедукции с индукцией дает возможность открыть законы сложных явлений. «Дедуктивному методу, характеризованному указанным способом, с его тремя составными частями: индукцией, рассуждением и проверкой», говорит Милль, «человеческий ум обязан своими наиболее блестящими победами в исследовании природы. Мы обязаны ему всеми теориями, подводящими обширные и сложные явления под несколько простых законов, которые никогда не могли бы быть открыты прямо».

130

 

 

Вопросы для повторения. В каких двух случаях употребляется дедуктивный метод? В чем заключается дедуктивное объяснение законов? Какое различие между законами эмпирическими и производными? Какие существуют три вида дедуктивного объяснения законов? Какое имеет значение сведение эмпирического закона на производный? В чем заключается дедуктивное открытие законов природы?

 

ГЛАВА 23-я.

О гипотезе.

Роль гипотез в науке. Некоторые ученые утверждали, что науки строятся исключительно благодаря собиранию фактов; по их мнению, в науке факты и опыты есть все; истинный ученый должен ограничиться только регистрированием фактов, т.-е. простым описанием фактов, событий, явлений. Но на самом деле это мнение совершенно неправильно. Ведь для того, чтобы собирать факты и материалы для науки, мы должны руководиться известной мыслью, известным планом: для того, чтобы приступить к совершению того или иного эксперимента, у нас должно быть известное соображение или рассуждение, почему мы должны произвести именно этот, а не какой-нибудь другой эксперимент. Если бы мы стали производить эксперименты наудачу, то это не привело бы ни к каким благоприятным результатам. Этим, по справедливому замечанию Джевонса, можно объяснить «весьма малые приращения, сделанные к нашему знанию алхимиками. Многие из них были люди очень проницательные и неутомимые; труды подобных лиц длились несколько столетий, они открыли немногое; а верный взгляд на природу дает современным химикам возможность открыть в течение года больше полезных фактов, чем сколько их было открыто алхимиками в течение многих столетий». Следовательно, не из собирания фактов наудачу создается наука, а из собирания, руководимого известным планом: ученый, приступающий к какому-нибудь исследованию, всегда должен приступать к нему с определенным планом. Для того, чтобы иметь план, необходимо построить гипотезу.

Но что такое гипотеза?

131

 

 

Определение гипотезы. Гипотезой называется предположение, которое мы считаем истинным для того, чтобы вывести из него следствия, согласные с действительными фактами или с другими проверенными положениями. Это согласие с фактами или с проверенными положениями служит доказательством гипотезы.

Когда мы прибегаем к гипотезе? Когда у нас есть ряд фактов, которые не объяснены, и именно потому, что в непосредственном опыте имеется недостаточно данных. В таком случае нам приходится дополнять данные опыта при помощи того, что не дано прямо в опыте. Это дополнение мы производим при помощи предположения, или гипотезы.

Процесс построения гипотезы во многих отношениях сходен с рассмотренным нами дедуктивным методом открытия законов. Разница между ними следующая. В процессе построения гипотезы отсутствует первая часть дедуктивного метода, именно отсутствует индукция, при помощи которой устанавливается закон, но гипотетический метод вполне тождествен с дедуктивным в том отношении, что пользуется приемом силлогизации и проверки. Закон же, из которого делается вывод, вместо того, чтобы доказываться, как это мы имеем в дедуктивном методе, просто принимается за истинное. Очевидно, что гипотеза может считаться истинной только в том случае, если она приводит к истинным результатам.

И так, в процессе построения гипотезы мы можем различать три стадии:

1) Мы делаем известное предположение.

2) Из этого предположения мы выводим следствия одно или несколько.

3) Смотрим, соответствуют ли эти следствия действительности или другим доказанным положениям.

Рассмотрим гипотезу всеобщего тяготения, чтобы дать представление о том, как гипотеза может проверяться своими собственными следствиями и реальными фактами. Как известно, согласно гипотезе тяготения, «все тела притягиваются друг к другу с силою, зависящею от их масс и от расстояния между ними». Согласно этой гипотезе все тела падают на землю; равным' образом все небесные светила притягиваются друг к другу. Посмотрим, как доказывается эта гипотеза.

132

 

 

Рассмотрим первое следствие этой гипотезы—именно падение тел на землю. По-видимому, нет ничего проще того положения, что вообще все тела падают на землю, однако, например, грекам это положение не казалось верным, потому что они имели случай наблюдать, что пламя, дым, водяные пары поднимаются кверху. На этом основании Аристотель и другие греческие философы предполагали, что некоторые вещи по природе своей тяжелы и стремятся книзу, тогда как другие вещи природы легки и стремятся кверху. Но Ньютон показал, что это предположение неверно, что нет тел легких и тяжелых по природе, что все тела, и в том числе т. наз. легкие, стремятся падать на землю: нар, дым хотя и поднимаются вверх, однако вполне подчиняются закону тяготения. Чтобы это было понятно, обратим внимание на следующее. Если мы положим на одну чашку весов фунтовую гирю, а на другую чашку полуфунтовую, то последняя поднимается кверху. Из того, что полуфунтовая гиря поднимается кверху, не следует, что она не подчиняется закону тяготения. Если, далее, мы погрузим в сосуд с водою кусок железа, то он, погружаясь в воду, заставит подняться часть жидкости вверх. Если мы погрузим в воду пробку, то пробка будет стремиться падать вниз, но, подобно только что упомянутой чашке весов, она будет поднята кверху. Из этого не следует, что пробка не стремится вниз; она только выталкивается вверх другим телом, которое стремится вниз с большей силой. Из этих примеров становится ясным, что пламя, пар и т. п. точно так же поднимаются, будучи легче окружающего воздуха. Поэтому Аристотель был неправ, предполагая, что есть тела, которые по своей природе стремятся вверх. На самом деле и эти тела стремятся к земле. Таким образом, если мы сделаем предположение, что все тела притягивают друг друга, то из этого предположения должно следовать, что все тела должны падать на землю, и, действительно, этот вывод из допущенного предположения согласуется с фактами: все тела стремятся падать на землю.

Рассмотрим второе следствие. Если все тела притягиваются друг другом, то все тела должны притягиваться к земле. Луна есть тело, и она должна притягиваться к земле, т.-е. падать па землю. Отчего же луна не падает на землю, а

133

 

 

продолжает вращаться вокруг нее? По теории Ньютона, луна действительно стремится упасть на землю, потому что если бы она этого не делала, то она должна была бы полететь, благодаря центробежной силе, по линии касательной к орбите. Ньютон при помощи вычисления показал, что если сила тяготения такова, какой он ее считает, то луна должна совершать путь около земли как раз именно тот, который она в действительности совершает. Он показал также, что планеты должны вращаться около солнца так, как они это делают.

Мы вывели два следствия из гипотезы всеобщего тяготения (падение тел, движение тел), и оказалось, что оба эти следствия соответствуют действительности. Эта гипотеза, следовательно, совершенно согласна с фактами; она объясняет эти последние, а следовательно, доказывается этими последними.

Experimentumcrucis. Иногда случается, что две или даже три совершенно различных гипотезы кажутся согласными с известными фактами, так что мы затрудняемся относительно того, которую из них следует считать истинной. Тогда наша задача сводится к тому, чтобы отыскать такой факт, который находился бы в согласии с одной гипотезой и противоречил бы другой. Нахождение такого факта называется Experimentumcrucis.

Для объяснения движения планет солнечной системы Декарт предполагал, что существует вихрь, который увлекает все планеты вокруг солнца в одном направлении. Для пояснения этого возьмем стакан с водою, в котором пусть плавают частички пробки, и затеи произведем движение, например, помешаем ложкой; тогда образуется водоворот, и в этом водовороте частички будут двигаться в одном направлении. Таким же образом, по Декарту, плавают и планеты в мировом пространстве, так как они, будучи раз приведены в движение, движутся в одном и том же направлении. Но Ньютоновская гипотеза тяготения объясняла те же самые факты, и было трудно решить, которая из двух гипотез правильнее. Поэтому необходимо было открыть какой-нибудь такой факт, который объяснялся бы одной гипотезой и находился бы в противоречии с другой. Такой факт оказался. Именно, Ньютон, показал, что движение комет не находится в согласии

134

 

 

с теорией Декарта. Кометы движутся не в том направлении, в каком движутся планеты, а проходят через весь круговорот солнца (см. рис. 31). Если бы правильна была гипотеза Декарта, то кометы должны были бы, увлекаемые общим вихрем, двигаться в том же направлений, в каком двигались планеты. Этим фактом опровергалась гипотеза Декарта. Но с гипотезой тяготения движение комет находилось в полном согласии.

Мы рассмотрели таким образом научное значение гипотезы; мы видели, что гипотеза приемлема только в том случае, если выводы из нее находятся в согласии с фактами. Но следует заметить, что гипотеза обладает всегда только лишь большей или меньшей степенью вероятности. Вероятность гипотезы может превратиться в достоверность, когда удается доказать, что данная гипотеза является единственным объяснением какого-либо явления, или если выводы из нее согласуются с другими признанными положениями, т.-е. с положениями, которые уже доказаны. О такой гипотезе можно сказать, что она проверена, доказана; доказанная же гипотеза называется теорией.

Гипотетический метод употребляется как в науках о природе, так и в науках о духе (истории, истории культуры, лингвистике и в истории литературы). Например, гипотеза о происхождении того или другого народа (о происхождении варягов), гипотеза о принадлежности сочинения тому или другому автору. Гипотеза употребляется также в судебных разбирательствах. На основании свидетельских показаний, которые имеют отрывочный характер, мы при помощи различных дополнений строим известную картину происшествия. Затем смотрим, оправдывается ли наше предположение теми или другими данными.

Вопросы для повторения. Как определяется гипотеза? Какое сходство и различие между методом дедуктивным и гипотетическим? Объясните на примере сущность гипотезы. Что такое Experimentum crucis? Объясните на примере. Какое отношение между гипотезой и теорией?

135

 

 

ГЛАВА 24-я.

Классификация.

Определение классификации. Мы в этом месте рассмотрим процесс классификации, потому что он служит вспомогательным средством для индукции; с другой стороны, как мы сейчас увидим, классификация возможна только благодаря индукции. Классификацией мы называем распределение вещей по классам согласно сходству между ними. Так, например, мы можем отнести «зарево», «кровь», «вишни» в один класс, потому что все они при всем различии имеют то общее, что они суть красного цвета. Классификация вещей, или распределение их по классам преследует свои определенные задачи, которые можно так формулировать: задача классификации заключается в том, чтобы распределить вещи на группы так, чтобы эти группы мыслились в порядке, который наиболее полезен для припоминания вещей и для определения свойств их.

Первое требование хорошей классификации заключается в том, чтобы пункты сходства, на основании которых мы составляем классы, были важны в практическом отношении.

Второе требование хорошей классификации состоит в том, чтобы она давала нам возможность сделать наибольшее число утверждений. Та классификация наилучшая, в которой предметы сходны друг с другом в возможно большем числе признаков.

Из этого становится ясной связь классификации с индукцией. Именно классификация предполагает индукцию, потому что эта последняя определяет те общие признаки, которые дают возможность относить их в общий класс. Только что указанный признак классификации отличает естественную классификацию от искусственной. Чтобы понять это, возьмем пример какой-нибудь искусственной классификации. Мы можем распределить фамилии каких-либо авторов по первым буквам их фамилий. Это иногда очень важно потому, что мы можем в случае надобности отыскивать те или иные фамилии. Но такая классификация допускает чрезвычайно мало утверждений. В самом деле, что мы можем утверждать относительно того или иного автора только на том основании, что фамилия его начинается с буквы А или с буквы В?

136

 

 

Естественная классификация. Для того чтобы мы могли делать большое число утверждений, мы должны брать за основание классификации такие признаки, которые влекут за собою большое число других признаков. Это бывает в том случае, когда мы соединяем предметы в общие классы по признакам существенным, выражающим природу вещей. Если мы имеем такую классификацию, то для нас вполне достаточно знать название класса, чтобы судить о свойствах вещей, принадлежащих к этому классу.

Возьмем пример для пояснения этого. Рожь, ячмень, овес и др. сорта хлеба относятся к семейству злаков. Всякий, кто знаком с ботаникой, легко может определить, принадлежит ли данное растение к злакам или нет. В пищу как людям, так и животным главным образом идет какой-нибудь род злаков, и поэтому следует предположить, что ни одно из растений, принадлежащих к этому семейству, не ядовито. Предположим, что путешественник попал в какую-нибудь необитаемую страну и нуждается в пище. Если он видит какой-либо злак, то он может питаться его семенами, потому что они не ядовиты. Следовательно, по принадлежности известного растения к известному классу можно умозаключать о ядовитости или неядовитости его.

Таким образом, естественная классификация имеет в виду раскрыть истинные свойства вещей и основывается вследствие этого на признаках важных и существенных. Поэтому с точки зрения этой классификации людей можно классифицировать по религии, речи, государственному устройству и т. п. Если бы мы стали делить людей на классы, смотря по тому, как они изготовляют пищу или как они одеваются, то это было бы искусственной классификацией.

Искусственная классификация. Искусственная классификация кладет в основу классификации какие-либо произвольные признаки. Так, например, известная Линнеевская система классификации растений может служить примером искусственной классификации. Шведский ботаник Линней разделил все растительное царство на 24 класса на основании числа тычинок, их прикрепления, срастания между собою и т. п. В искусственной классификации вследствие того, что она имеет в своей основе более или менее случайный при-

137

 

 

знак, всегда возможно, что совершенно несходные предметы могут очутиться в одной группе, между тем как очень родственные предметы могут очутиться в очень отдаленных группах. В Линнеевской классификации очень родственные группы растений, например, «злаки», относятся в различные очень несходные классы, между тем как очень несходные, например, дуб и один вид осоки, соединяются в один класс. Это происходит вследствие того, что в основе этой классификации лежит только такой признак, как строение цветка. Этого не может быть в естественной классификации, в которой для выяснения родства между растительными формами обращают внимание на всю совокупность признаков, свойственных изучаемым организмам. Другой пример. Семейство губоцветных характеризуется четырехгранным стеблем, супротивными листьями, двугубым зевообразным венчиком и четырьмя тычинками. Но есть растение (шалфей), которому присущи все указанные черты, но в котором всего две тычинки. Вследствие этого его приходится отнести в другое семейство, если пользоваться искусственной классификацией, хотя родство его с губоцветными не подвергается никакому сомнению.

[В связи с классификацией следует упомянуть о научной номенклатуре и научной терминологии.

Номенклатура. Номенклатура самым теснейшим образом связана с классификацией. Группы естественные или искусственные, на которые распределяются предметы, не могут быть нами запоминаемы, не могут быть сообщаемы другим, если только эти группы не фиксируются, благодаря тому, что им даются названия. Для этого существует именно номенклатура. Номенклатура может быть определена, как собрание названий всех реальных родов, классов, например, в ботанике, зоологии и химии и т. п. В минералогии названия отдельных минералов, каковы, например, гематит, топаз, амфибоз, составляют номенклатуру. В химии мы имеем названия, напр., для органических соединений: этил, ацетил, бензол и т. п. Число естественных групп в природе настолько велико, что почти невозможно запомнить имена отдельных групп. Так, известные науке виды растений значительно превосходят 60.000, но если мы примем в соображение разновидности и подразновидности, то число групп будет

138

 

 

значительно больше. Поэтому только при помощи названий и возможно оперировать с таким огромным числом предметов. Мы можем не помнить подгруппы, но если мы помним группу, то этого вполне достаточно для оперирования с ними. В пример можно привести номенклатуру, введенную Линнеем в ботанику. Эта номенклатура была в состоянии обозначить около 10.000 видов растений 1.700 родовыми названиями, которым придавались видовые признаки. Так, например, в ботанике каждое растение обозначается двойным названием: одно из них есть родовое, т.-е. указывает род, другое видовое. Например, в названии Betula alba, Betula есть название всего рода берез, alba есть название вида. Может быть десять видов герани; эти виды каждый в отдельности нам нет надобности запоминать: достаточно помнить только род. Всякая хорошая номенклатура предполагает хорошую систему классификации. Только те науки, которые имеют полную классификацию, имеют и выработанную номенклатуру, например, ботаника и химия.

Терминология. Терминология есть совокупность названий или терминов, которые отличают те или другие свойства или части индивидуальных предметов, рассматриваемых наукой. Различие между номенклатурой и терминологией сводится к следующему. Если мы говорим о роде «роза», то мы употребляем номенклатуру ботаники; если же мы говорим о свойствах индивидуума вида «роза», то мы употребляем не номенклатуру, а терминологию. Термины дают нам возможность описывать индивидуальные предметы. «Описательная терминология, по Юэллю, должна заключать в себе все термины, необходимые для того, чтобы точно описывать все то, что было наблюдаемо относительно какого-либо предмета или явления, для того, чтобы мы могли постоянно вспоминать о наблюденном. Для каждого качества, формы, обстоятельства, степени или количества должно быть подходящее название или способ выражения. Так, вспоминая открытие нового минерала, мы должны быть в состоянии фиксировать при помощи слова самым точным образом его кристаллическую форму, его цвет, степень его твердости, удельный вес, запах, вкус и т. п.». В ботанике, когда мы описываем листья того или другого растения, мы употребляем термины: «округлые»,, «овальные», «эллиптические», «продолговатые», «яйцевидные»,

139

 

 

«ланцетные», «линейные», «сердцевидные», «почковидные», «стреловидные», «копьевидные» листья и т. п.

Совершенная терминология должна быть построена таким образом, чтобы выражать каждый оттенок в описании тех или иных свойств. Прогресс наук задерживался вследствие того, что термины употреблялись без достаточной точности, например, в физике употреблялись не точно такие термины, как сила, притяжение и т. п.]

Вопросы для повторения. Что такое классификация и какие она преследует цели? Какие требования хорошей классификации? Какое отличие естественной классификации от искусственной? Что такое номенклатура и каково значение ее? Что такое терминология и чем она отличается от номенклатуры?

 

ГЛАВА 25-я.

О приблизительных обобщениях и об аналогии.

Индуктивный метод исследования является главным методом для открытия законов природы, но, как мы видели, им не всегда можно пользоваться: иногда приходится для той же цели пользоваться дедукцией, гипотезой; иногда приходится пользоваться также так называемыми приблизительными обобщениями и методом аналогии.

Приблизительные обобщения. Приблизительные обобщения суть умозаключения или утверждения, справедливые относительно большинства вещей данного класса. Приблизительные обобщения выражаются при помощи суждений, содержащих утверждение или отрицание относительно большинства вещей известного класса, так что формулой приблизительных обобщений будет:

„Большинство S суть P“.

Слово «большинство» в приблизительных обобщениях может заменяться также словами «большею частью», «обыкновенно», «вообще» и т. д. Если я скажу: «люди образованные в большинстве случаев менее склонны к пороку, чем люди необразованные», то я этим хочу сказать, что это справедливо только относительно большинства образованных людей, а не относительно всех. Приблизительные обобщения употребляются во всех тех случаях, когда мы не имеем воз-

140

 

 

можности точно определить причинную связь явлений. Они употребляются, например, в медицине. Взгляд на действие тех или других лекарственных веществ на организм выражается при помощи положений, имеющих характер приблизительных обобщений. Если мы говорим, что «бром успокаивает нервы», то это справедливо только относительно большинства людей, а не относительно всех. Наши взгляды на значение общественных мероприятий также выражаются при помощи приблизительных обобщений. Например, когда мы говорим, что те или другие учреждения имеют воспитательное значение, то мы имеем в виду только большинство людей, а не всех. Точно так же наши суждения о характере народов представляют собою приблизительные обобщения. Напр., когда мы говорим, что англичане предприимчивы, немцы трудолюбивы и т. п.

Значительная часть науки состоит из приблизительных обобщений, и в практической жизни мы поставлены в необходимость пользоваться приблизительными обобщениями. Это происходит от того, что явления жизни слишком сложны для того, чтобы мы могли найти какие-нибудь точные законы, а потому нам приходится довольствоваться приблизительными обобщениями.

Но приблизительные обобщения тем не менее бесспорно имеют научное значение. При научных исследованиях, относящихся к свойствам не отдельных индивидуумов, но к массам индивидуумов, как это мы имеем, например, в политических и социальных науках, мы можем пользоваться приблизительными обобщениями так как если бы это были обобщения, имеющие всеобщий характер. В самом деле, для государственного человека вполне достаточно знать, что «большинство» людей действует таким-то и таким-то образом, так как для его деятельности является важным то, как действует и чувствует большинство. Напр., Кобдэн, проводя свой закон о хлебных пошлинах, знал, что этот закон разорит меньшинство (богатых землевладельцев), зато поднимет экономическое благосостояние масс, а этого было вполне достаточно, чтобы провести реформу.

Эти соображения опровергают общераспространенное мнение, что выводы политических и социальных наук, как не вполне достоверные, не имеют научного значения. Несомнен-

141

 

 

но, конечно, что эти науки должны быть в отношении достоверности поставлены ниже естественных наук, потому что их явления не могут быть предсказываемы с тою точностью, с какой предсказываются явления, составляющие предмет изучения естествознания; но тем не менее нет основания думать, чтобы достигнутые этими науками истины заслуживали меньшого внимания или были менее научными.

Вычисление вероятности. Говоря о вероятности приблизительных обобщений, в отличие от достоверности индуктивных умозаключений, мы рассмотрим в связи с этим, что называется вероятностью и достоверностью наступления какого-либо события.

Для того, чтобы показать, каким образом определяется степень вероятности наступления какого-либо события, возьмем пример. Положим, перед нами находится ящик с белыми и черными шарами, и мы опускаем руку, чтобы вынуть оттуда какой-либо шар. Спрашивается, какова степень вероятности того, что мы вынем белый шар. Для того, чтобы определить это, мы сосчитаем число шаров белых и черных. Предположим, что число белых шаров будет 3, а число черных 1; тогда вероятность, что мы вынем белый шар, будет равна ¾, т.-е. из 4 случаев мы имеем право рассчитывать на три благоприятных и один неблагоприятный. Вероятность, с какой вынется черный шар, будет выражаться ¼, т.-е. из четырех случаев можно рассчитывать на один благоприятный. Если в ящике находятся четыре белых шара, то вероятность, что будет вынут белый шар, будет выражаться числом 4/4 = 1. Степень вероятности, выражаемая 1, есть достоверность. В самом деле, из ящика, в котором находятся только белые шары, мы наверное вытянем белый шар.

Если же мы не имеем возможности определять отношения благоприятных и неблагоприятных случаев, тогда для определения степени вероятности наступления данного события следует определить максимум и минимум повторения разбираемого случая. Средняя величина повторений укажет среднюю вероятность. Таким способом статистика определяет степень вероятности смерти для человека известного возраста в известной местности. На этом вычислении, как известно, основывается существование обществ страхований жизни.

142

 

 

Аналогия. Перейдем к рассмотрению умозаключения по аналогии и его отношения к индукции. Как мы видели, индукцией называется умозаключение от частных положений к общему. Аналогией мы называем умозаключение, в котором от сходства двух вещей в известном числе свойств мы заключаем к сходству в других свойствах. Из сходства в одной части признаков мы умозаключаем к существованию сходства в другой части признаков. Например, Марс похож на землю в части своих свойств. Именно, Марс обладает атмосферой с облаками и туманами, совершенно похожими на наши. Марс имеет моря, отличающиеся от суши зеленоватым цветом, и полярные страны, покрытые снегом. Отсюда мы заключаем, что Марс похож на землю и в других свойствах и именно, что он, подобно земле, обитаем. Таким образом населенность Марса есть умозаключение по аналогии.

Отсюда видно, что между индукцией и аналогией существует некоторое сходство.

И в индукции, и в аналогии мы умозаключаем от частностей; но разница между ними та, что индукция приходит к общему, а умозаключение по аналогии приходит опять к частности. Умозаключение по аналогии не обращается к какому-нибудь определенному общему закону. В умозаключении по аналогии мы умозаключаем не от ряда случаев, но от известного числа пунктов сходства.

Заключение по аналогии не может дать ничего, кроме вероятности. Степень вероятности умозаключения по аналогии зависит от трех обстоятельств: 1) количества усматриваемых нами сходств, 2) количества известных несходств между ними и 8) объема нашего знания сравниваемых вещей. Именно, вероятность заключения по аналогии может считаться очень высокой, если число пунктов сходства между рассматриваемыми вещами очень велико и если в то же время число пунктов несходства незначительно, но при этом мы знаем, что число известных нам свойств изучаемой вещи достаточно велико. Чем больше число неизвестных свойств, тем меньше достоверность нашего вывода. Если мы находим, что В сходно с А в 9 из 10 известных свойств, то вероятность, что оно будет сходно и в других отношениях, будет равна 9:10. Достоверность,

143

 

 

присущая умозаключению по аналогии, таким образом, может иметь различные степени.

О научных достоинствах метода аналогии можно сделать следующее замечание. Иногда заключения, полученные посредством аналогии, так и остаются на степени только лишь вероятного предположения; иногда же они, делаясь основой для гипотез, получают свое оправдание в фактах и выводах, превращаются, следовательно, в научные теории. Поэтому легко видеть, что заключения по аналогии могут быть весьма ценными в научном отношении, так как они являются, так сказать, предварительными построениями, указывающими, куда должен направить свое внимание исследователь.

Вопросы для повторения. Что такое приблизительные обобщения и чем они отличаются от индукции? Как вычисляется вероятность? Что такое умозаключение по аналогии и чем оно отличается от индукции? От чего зависит степень вероятности умозаключения по аналогии?

 

ГЛАВА 26-я.

О доказательстве, методе и системе.

Определение доказательства. Мы уже имели случай употреблять понятие доказательства в связи с понятием умозаключения. Теперь мы дадим его определение и укажем, какое существует различие между доказательством и умозаключением.

Мы видели, что суждения могут быть непосредственно очевидными, или они могут сделаться очевидными, если мы их сведем к положениям, которые имеют характер непосредственно очевидный. Если мы при помощи такого приема делаем суждения очевидными, то можно сказать, что мы их доказываем. Это приведение к очевидности облекается в силлогистическую форму, так что доказательство может быть определено, как выведение какого-либо суждения из других суждений, признанных истинными и очевидными.

Таким образом доказательство вообще имеет форму силлогистического умозаключения, но есть существенные пункты отличия между умозаключением и доказательством. Именно в умозаключении мы не всегда обращаем внимание на то,

144

 

 

истинны ли посылки; в доказательстве же истинность посылок является самым главным требованием. Кроме того, доказательство отличается от силлогизма еще и тем, что в нем доказываемое суждение, соответствующее заключению силлогизма, известно заранее.

Во всяком доказательстве мы различаем три части: 1) доказываемое положение или тезис; это именно то, что должно быть доказано, или сделано очевидным; 2) основы доказательства или аргументы; это то, при помощи чего тезис доказывается или делается очевидным; 3) форма доказательства или способ, каким тезис выводится из аргументов. Тезис доказательства соответствует заключению в силлогизме. Аргументы соответствуют посылкам силлогизма. Форма доказательства есть логическая схема, при помощи которой выводится заключение. Напр., нужно доказать, что «железо плавко». Это есть тезис. Для доказательства нам необходимо воспользоваться следующими двумя аргументами: «все металлы плавки», «железо есть металл». Построивши силлогизм, мы докажем наш тезис.

Основные принципы и аксиомы. Мы видим таким образом, что доказательство сводится к раскрытию очевидности данного суждения из очевидности других суждений, которые называются аргументами. А если эти последние не очевидны, то как поступить в таком случае? Нужно доказать их в свою очередь при помощи каких-либо других аргументов.. Но так как эти последние также могут быть сомнительными, то доказательство большею частью представляет целую цепь умозаключений. В конце концов всякое доказательство должно приводить к таким положениям, которые имеют уже бесспорный или очевидный характер. Эти последние или суть аксиомы, или это суть общепризнанные общие положения, которые в таком случае называются основными принципами.

Прямое и косвенное доказательство. Процесс доказательства может быть прямой или косвенный. В прямом доказательстве мы выводим истинность тезиса из истинности аргументов при помощи умозаключения; непрямое или апагогическое доказательство выводит истинность тезиса из невозможности допустить или признать истинность положения, противоречащего тезису. Имен-

145

 

 

но, не в прямом доказательстве мы берем положение, противоречащее тезису, и предполагаем его истинным. (Такое положение называется антитезисом.) Затем из этого положения выводим следствия, которые приводят к противоречию с данными или признанными положениями. Вследствие этого нам приходится отвергнуть истинность противоречащего положения, которое мы предположительно допустили, а отсюда будет следовать истинность тезиса. Таким образом доказывается тезис.

Возьмем пример из математики. Требуется доказать, что в треугольнике, в котором два угла равны, противолежащие им стороны также равны. Пусть в треугольнике ABC угол αравняется углу ß и пусть противолежащие им стороны будут АС ж ВС. Нам нужно доказать, что АС = ВС. Это есть тезис. Возьмем положение, противоречащее тезису: «АС не равняется ВС». Это будет антитезис; тогда из этого последнего положения (согласно теореме, что во всяком треугольнике против большого угла лежит большая сторона) будет следовать, что угол α должен быть или больше или меньше ß. Но так как этот вывод противоречит принятому нами положению, то антитезис является ложным; тогда истинным должно быть положение, противоречащее ему, именно тезис. Такого рода доказательство называется также reductio ad impossibile или reductio ad absurdum.

Понятие o методе и системе. Для достижения определенных целей в процессе мышления те или другие суждения или ряд суждений должны располагаться в определенном порядке, сообразно известным правилам. Этот порядок расположения суждений, способствующий достижению определенной цели, называется методом. Как мы уже видели, для того, чтобы доказать существование причинной связи между явлениями, нужно, чтобы наши суждения располагались в том или другом порядке: или по методу сходства, или по методу разницы и т. п. Понятие «метод» употребляется и по отношению к физическим процессам. Например, можно учиться плавать, руководясь определенным правилами. Это будет методическое обучение, но можно учиться без всяких правил— это будет неметодическое обучение.

Системой вообще мы называем соединение взаимосвязанных , явлений в одно целое. Суждения, конечно, тоже могут

146

 

 

соединяться таким образом, чтобы составлять одно целое; тогда они образуют «систему» суждений. Система суждений составляет науку. Наука, таким образом, есть совокупность систематически расположенных суждений достоверных или, по крайней мере, вероятных.

Научное мышление должно осуществляться сообразно с известными правилами, т.-е. по определенному методу. В научном мышлении метод может применяться в двух различных случаях, именно, во-1-х, в открытии новых истин и, во-2-х, в определенном расположении уже открытых истин, как это бывает в изложении научных данных для наиболее ясного их понимания. И для открытия, и для изложения научных истин служат методы аналитический и синтетический.

Анализ и синтез. Для того, чтобы понять, в чем заключаются эти методы, заметим, что частное положение, вывод, следствие находится в таком же отношении к общему положению, принципу, основанию, в каком действие находится к причине. Как из известной причины получается известное действие, так из известного принципа, основания получается известный вывод, следствие. Мы так же ищем для известного положения принцип или основание, как для известного действия ищем его причину. С другой стороны, как для известной причины мы ищем его действие, так для известных принципов мы можем искать их следствия.

Отсюда в зависимости от того, что мы ищем, получаются два различных процесса.

Если мы от причины идем к действию, от основания к выводу, то такой путь называется прогрессивным или синтетическим. Прогрессивным он называется потому, что он соответствует реальному ходу природы, действительному ходу вещей, так как в природе причина раньше, чем действие. Обратный путь, именно от действия к причине, от выводов к принципам называется регрессивным, аналитическим.

147

 

 

Часто словам анализ и синтез придают другое значение, и именно под анализом понимают метод разложения целого на его составные части, а под синтезом—обратный метод сложения целого из его частей или элементов. В этом смысле чаще всего говорят об анализе и синтезе химическом. Но для того, чтобы истинный смысл понятий анализ и синтез, как он употребляется в научном исследовании и изложении, был ясен, нужно считать основным значением слова анализ то, которое мы только что указали, именно сведение частных положений к основным принципам, а под синтезом следует понимать выведение следствий из основных принципов *).

Аналитический метод исследования мы употребляем тогда, когда мы ищем причины данных действий. Судья, моралист и др., которые ищут причины известных действий, употребляют метод аналитический; законодатель, политик, педагог, которые стараются предусмотреть действия известных причин, должны идти путем синтетическим.

Для объяснения применения анализа возьмем следующий пример. Чтобы решить задачу вписывания правильного шестиугольника в данный круг, мы рассуждаем так: предположим, что задача решена, и пусть АВ будет одной из сторон вписанного шестиугольника. Если мы проведем радиусы к конечным точкам сторон, то треугольник, образовавшийся таким образом, будет равноугольный (так как каждый угол равен ²/з прямого угла); следовательно, сторона правильного вписанного шестиугольника равна радиусу. Отсюда следует, что для того, чтобы вписать правильный шестиугольник в данный круг, нужно радиус нанести шесть раз на окружность. Здесь применение аналитического метода очевидно. Мы, сделавши предположение, что задача решена, т.-е. допустивши данное частное положение,

*) Термин анализ, как он употреблен здесь, находится в согласии с тем, как его употребляли Аристотель и последующие писатели. По Аристотелю, ἄναλύειν (разлагать) значило сводить сложное к элементам, как к их причинам (или принципам), приводить к началу, к первоначальным элементам. Подобно тому, как геометр, чтобы познать сложные геометрические фигуры, разлагает, сводит их на элементы, напр., многоугольник на треугольник, так и в том случае, если нам нужно понять какой-нибудь частный случай, мы должны его свести к основному принципу, объясняющему его.

148

 

 

нашли то условие, тот общий принцип, при котором это частное положение возможно, т.-е. из которого это положение можно вывести. Другими словами, мы данное частное положение сводим к общему принципу.

Примером применения синтеза может служить теорема: «во всяком треугольнике сумма его углов равняется двум прямым углам». Для доказательства этой теоремы мы должны принять следующих два общих положения: «внутренние накрест лежащие углы равны» и «всякая нара смежных углов равна двум прямым». Из этих общих положении мы выводим искомое положение.

Отношение анализа и синтеза к индукции и дедукции. Но спрашивается, в каком отношении находятся методы аналитический и синтетический к методам индуктивному и дедуктивному? Отношение между ними таково, что анализ соответствует индукции, а синтез соответствует дедукции. Что анализ соответствует индукции, легко пояснить следующим образом. Индукция имеет целью открытие законов, общих принципов. В процессе индукции мы идем от частных положений к общим принципам. Поэтому в процессе индукции мы совершаем регрессивный путь. Из этого следует, что индукция соответствует анализу.

Наоборот, дедукция выводит из общих принципов частные положения, те или иные следствия. Из этого становится ясным родство дедуктивного метода с синтетическим. Синтетический метод состоит в том, что мы предполагаем известные принципы открытыми и доказанными; из этих общих принципов мы выводим следствия.

Вопросы для повторения. Что такое доказательство и чем оно отличается от силлогизма? Какие три части отличаем мы в доказательстве? Что такое основные принципы? Какое доказательство называется прямым? Какое доказательство называется косвенным? Изложите ход косвенного доказательства. Что называется методом? Что называется системой? В каких двух случаях употребляется метод в научном мышлении? Какие методы называются аналитическим и синтетическим? Почему эти методы называются прогрессивным и регрессивным? Покажите применение методов аналитического и синтетического в математике. Какое существует отношение между методами аналитическим и синтетическим и методами индуктивным и дедуктивным?

149

 

ГЛАВА 27-я.

О логических ошибках.

Обыкновенно принято логические ошибки делить на две группы: на ошибки логические в собственном смысле и ошибки, происходящие вследствие неправильности в словесном выражении мысли. В первом случае ошибка заключается в неправильности логического процесса, во втором случае—в неправильности выражения. Из ошибок по словесному выражению заметим следующую:

Homonymia—ошибка, которая происходит вследствие того, что одно и то же слово служит для обозначения различных понятий, т.-е. употребляется в различных значениях. Например, многие думают, что «материализм» метафизический есть то же самое, что и «материализм» экономический. В этом случае происходит смешение понятий вследствие смешения слов. Другие ошибки, происходящие вследствие неправильностей в словесном выражении мысли, указываются в грамматике.

Для того, чтобы понять, благодаря чему логические ошибки получают то или иное обозначение, вспомним обозначение частей доказательства. В доказательстве мы различаем: тезис, аргументы и форму доказательства. Ошибки могут быть по отношению к каждой части доказательства. Из предыдущего ясно, что если взять ложные аргументы, то получится ошибка; но ошибка может быть и в том случае, если форма умозаключения будет неправильная.

Ошибки дедукции. Логические ошибки могут быть по отношению к тезису.

Если доказывается не то, что требовалось доказать, то такая подмена тезиса называется ignoratio elenchi (elenchus означает опровержение какого-либо аргумента, a ignoratio elenchi означает незнание того силлогизма, которым можно опровергнуть противника). Например, если нужно доказать, что что-либо несправедливо в моральном смысле, а кто-нибудь доказывает, что это несправедливо в юридическом смысле, то он вместо одного доказывал бы совсем иное, хотя и сходное, Если доказывается что-либо отличное по роду от того, что нужно доказать, то это будет ошибкой μετάβασις εἰς

150

 

 

αλλο γένος. Если бы, например, кто-нибудь хотел доказывать невиновность обвиняемого тем, что другие совершили то же самое преступление, но избегли наказания.

Уклонение от тезиса может происходить еще и в том смысле, что доказывается слишком мало, так что тезис частью остается недоказанным, или доказывается слишком много, так что из данных оснований следует не только тезис, но и какое-нибудь ложное положение. Такое ошибочное доказательство называют Qui nimium probat, nihil probat. Например, для доказательства положения, что сумма углов треугольника равняется двум прямым, недостаточно было бы доказывать, что эта сумма будет не больше 180 (здесь доказывается слишком мало). Если бы мы хотели доказать, что кто-нибудь добродетелен, и при этом стали бы доказывать, что о нем ничего неизвестно дурного, то этим доказывалось бы слишком мало. Если бы кто-нибудь стал доказывать недозволительность самоубийства на том основании, что человек не может у себя отнимать того, что он сам себе не дал, то доказывал бы слишком много, потому что из его доказательства выходило бы, что он не может резать ногтей, волос, что он не может продавать унаследованное или полученное в подарок и т. п. Поэтому он тезиса собственно не доказывает. Как легко видеть, такое ошибочное доказательство получается в том случае, когда приводятся положения, которые оказываются ложными при данной степени общности, но которые могли бы быть истинными при меньшей степени общности.

К этой же группе ошибок следует отнести ошибку, происходящую вследствие пользования приемом, который называется argumentumad hominem и который употребляется в том случае, когда вместо того, чтобы доказывать ложность какого-либо мнения, подвергают рассмотрению личность того, кто высказал это мнение. Если например, кто-нибудь желает доказать несостоятельность научной теории какого-либо писателя и вместо того, чтобы подвергать критическому разбору именно теорию автора, раскрывает принадлежность автора к несимпатичному для читателей политическому направлению, то он пользуется аргументом ad hominem. Это доказательство, логически самое слабое, фактически пользуется большим успехом.

151

 

 

По отношению к основаниям доказательства или аргументам могут быть следующие ошибки:

Основная ошибка, πρῶτονφεῦδος, error fundamentalis—ложное основное положение, на котором строится какое-либо доказательство и из которого могут делаться различные выводы. Например, основной ошибкой в астрономических рассуждениях до Коперника был аргумент, что солнце и звезды вращаются вокруг земли.

Ошибка petitio principii бывает тогда, когда для доказательства какого-либо положения мы кладем в основу доказательства такое положение, которое предполагает истинным доказываемое положение. Положим, кто-нибудь хочет доказать положение:

Тезис: „Все частички материи имеют один и тот же вес".

На вопрос, почему он так думает, он мог бы привести следующее

Основание доказательства: „Если мы возьмем два тела с одинаковым объемом, то окажется, что то тело, которое тяжелее, имеет большее число частичек, т.-е. больший вес зависит от количества частичек“.

На вопрос, откуда же известно, что больший вес тела с одинаковым объемом зависит именно от количества частичек, он ответит:

„Если принять в соображение, что все частички материи имеют одинаковый вес, то сделается вполне очевидным, что чем тело тяжелее, тем большее число частичек в нем содержится при одинаковом объеме“.

В этом примере тезис доказывается при помощи положения, которое само может быть доказано при допущении истинности тезиса.

Таким образом в ошибке petitio principii мы принимаем за истинное то положение, которое должно быть доказано.

Родственными с petitio principii являются ошибки: idemper idem и circulus in demonstrando. Ошибка idemperidem, когда какое-либо положение доказывается посредством этого самого положения. Например, на вопрос, почему мы видим сквозь стекло, иногда отвечают, потому что оно прозрачно; но очевидно, что назвать вещество прозрачным значит, другими словами, сказать, что сквозь него можно видеть.

152

 

 

Ошибкой circulus in demonstrando называется тот случай, когда тезис А доказывается посредством аргумента В, который в свою очередь доказывается посредством аргумента А. Например, мы утверждаем, что сочинение того или иного писателя заслуживает доверия, потому что он правдив. Нас спрашивают: «откуда вам известно, что этот писатель правдив?» и мы отвечаем: «это доказывается содержанием его сочинений». В этом случае мы делаем круг в доказательстве.

Особняком стоят след. ошибки.

Ошибка a dicto secundum quit ad dictum simpliciter возникает в том случае, когда выражение, взятое в условном, относительном  смысле, принимается затем в смысле безусловном. Например, мышьяк, стрихнин, синильная кислота, будучи введены в организм в значительном количестве, причиняют смерть. Мы в данном случае об этих веществах говорим в условном смысле, т.-е. говорим о них, что они введены в организм «в значительном количестве». Но если бы мы сказали, что они всегда причиняют смерть, то мы допустили бы указанную ошибку, потому что в очень малых дозах они не смертельны и, как известно, употребляются в качестве лекарств. Во втором случае мы отбросили то условие, которое поставляли в первом случае.

Ошибка fallacia a sensu composito ad sensum divisum происходит вследствие смешения термина собирательного с термином общим. Когда мы употребляем общий термин, то, то, что справедливо относительно целого класса, обозначаемого общим термином, справедливо и относительно каждого индивидуума, входящего в этот класс; но когда мы употребляем собирательный термин, то это может быть несправедливо. То, что справедливо относительно целого, обозначаемого собирательным термином, то может быть несправедливо относительно вещей, входящих в это целое. Например, какое-нибудь общество, в котором я состою членом, приняло решение, заслуживающее порицания. Если бы кто-нибудь стал и меня упрекать за это решение, то он допустил бы ошибку fallacia a sensu composito ad sensum divisum, ибо это утверждение, справедливое относительно общества, взятого в целом, может быть совершенно несправедливо относительно

153

 

 

отдельных членов этого общества, которые могли подавать свой голос против указанного решения.

Fallacia a sensu diviso ad sensum compositum получается в том случае, когда мы о собирательном целом утверждаем то, что справедливо только относительно частей этого целого. Здесь происходит также смешение между термином общим и собирательным. В общих понятиях то, чего мы не можем сказать относительно индивидуума того или другого класса, мы не можем утверждать и о самом классе. В собирательных понятиях, наоборот, мы о частях собирательного целого можем утверждать много такого, чего не можем утверждать относительно целого. Например, кто-нибудь, рассуждая о своих расходах, может сказать: «этот расход меня не разорит», и о другом расходе скажет: «и этот расход меня не разорит». Если он будет рассуждать таким образом и обо всех остальных расходах, то он должен будет признать, что все расходы его не разорят, что будет ошибочно: то, что справедливо относительно каждого расхода, взятого в отдельности, может быть совсем несправедливо относительно всех расходов, взятых вместе. Другой пример. Больной хочет определить, смертельна ли его болезнь или нет; рассмотрев каждый симптом в отдельности, он находит, что каждый симптом в отдельности не смертелен; отсюда он делает вывод, что его болезнь не смертельна. Но это рассуждение может оказаться неправильным, потому что каждый симптом в отдельности может быть не смертельным, а все в целом могут быть смертельны.

Ошибки индукции. К ошибкам, связанным с индукцией, относятся прежде всего поспешные обобщения (fallacia fictae universalitatis). Когда путешественники после поверхностного знакомства с каким-либо народом делают попытки характеризовать его, например, когда они произносят: «русские лживы», «немцы жестоки» и т. п., то они впадают именно в ошибку поспешного обобщения.

Ошибка posthocergo propterhoc называется также ошибкой non causa pro causa. Если кто-нибудь заметил, что после какого-либо события возникает какое-либо действие, то он считает первое событие причиной, хотя в действительности, может быть, есть события, от которых данное событие на-

154

 

 

ходится в большей зависимости и которое собственно является истинной причиной данного действия. Когда после появления кометы возникали какие-либо несчастия, то обыкновенно комету считали причиной несчастий. Когда в трубке возникала пустота и вода в ней поднималась, то думали, что пустота есть причина поднятия воды. Если после введения какой-нибудь формы правления возникают какие-нибудь события, то обыкновенно эти формы правления и считаются причиной их, между тем как истинные причины, может быть, заключаются в чем-нибудь другом, напр., в определенной степени умственного или нравственного развития общества.

Есть случаи, которые особенно предрасполагают к тем или иным выводам. Это бывает обыкновенно тогда, когда у нас бывает почему-либо интерес помнить случаи, подтверждающие одно положение, и забывать случаи, опровергающие это положение. Если предсказание какого-нибудь календаря один раз сбывается, то необразованные люди склонны в этом случае черпать для себя уверенность в правдивости предсказания этого календаря, совсем упуская из виду тысячу случаев, в которых его предсказания не сбывались. На этом основана вера в различных предсказателей, шарлатанов и т. п.

Следует привести несколько примеров ошибок индукции по простому перечислению. Некоторые часто так рассуждают: «женщины никогда не равнялись мужчинам по энергии и уму; поэтому следует признать, что женщина вообще ниже мужчины». Но то положение, что до сих пор женщины в умственной жизни были ниже мужчины, есть положение эмпирическое, справедливое лишь для известного времени и при известных условиях. В другое время и при других условиях может быть совсем иначе. Ошибкой по простому перечислению нужно считать утверждение, что война всегда будет между народами, потому что до сих пор она всегда была.

Ошибка аналогии. В качестве примера ложной аналогии можно привести то умозаключение, по которому политические тела, подобно телам органическим, переживают юный и зрелый возрасты, старост и подвергаются смерти. Ошибкой аналогии нужно считать утверждение, что будто бы у муравьев есть рабы, воины, разведение домашних животных и т. п.

155

 

 

Софизмы. Те ошибки, которые совершаются непреднамеренно, называются паралогизмами, а те, которые совершаются преднамеренно для того, чтобы ввести кого-либо в заблуждение, называются софизмами. Приведем несколько примеров софизмов, идущих к нам из древности.

1) Софизм «лгун». Вполне возможно, что лгун сознается в том, что он лгун. В таком случае он скажет правду. Но тот, который говорит правду, не есть лгун. Следовательно, возможно, что лгун не есть лгун (какая ошибка?).

2) Софизм «рогатый». То, чего ты не потерял, ты имеешь; ты не потерял рогов. Следовательно, ты имеешь рога (какая ошибка?)

3) Софизм «куча». Будет ли куча песку, из которой мы взяли одну песчинку, считаться кучей? Да, будет. А если взять еще одну песчинку? Будет. Так как при последовательном отнятии по одной песчинке куча не перестает быть кучей, то одна песчинка должна называться кучей (какая ошибка?).

4) Софизм Эватла. Эватл брал уроки софистики у софиста Протагора под тем условием, что гонорар он уплатит только в том случае, если выиграет первый процесс. Ученик после обучения не взял на себя ведения какого-либо процесса и потому считал себя в праве не платить гонорара. Учитель грозил подать жалобу в суд, говоря ему следующее: «судьи или присудят тебя к уплате гонорара илине присудят. В обоих случаях ты должен будешь уплатить. В первом случае в силу приговора судьи,  во втором случае в силу нашего договора». На это Эватл отвечал: «ни в том, ни в другом случае я не заплачу. Если меня присудят к уплате, то я, проиграв первый процесс, не заплачу в силу нашего договора: если же меня не присудят к уплате гонорара, то я не заплачу в силу приговора суда». (Ошибка становится ясной, если мы раздельно поставим два вопроса: 1) должен ли Эватл платить или нет, и 2) выполнены ли условия договора или нет.)

Вопросы для повторения. На какие два класса делятся логические ошибки? Что такое homonymia? Что такое ignoratio elenchi? Что такое qui nimium probat nihil probat? Что называется доказательством ad hominem? Что называется основной ошибкой? Что такое petitio principii? Что такое idem

156

 

 

per idem? Что называетоя circulus in demonstrando? Какая ошибка называется fallacia a dicto secundum quit ad dictum simpliciter? Какая ошибка называется fallacia a sensu composito ad sensum divisum? Какая ошибка называется fallacia a sensu diviso ad sensum compositum? Перечислите, какие существуют ошибки индукции, и объясните их. Какое различие между софизмами и паралогизмами?

 

ГЛАВА 28-я.

О различии наук.

Рассмотрим различие, существующее между науками в отношении их достоверности, а также различие, вытекающее из различия их предмета. В этом отношении большое различие существует между науками математическими, естественно-историческими или науками о при, роде историческими.

Математика. Математика, сходная по своему предмету с логикой, стоит совершенно в стороне от других наук. Математика и логика (формальная) отличаются от всех других наук тем, что их положения отличаются аподиктически достоверным характером, их положения необходимы, т.-е. немыслимы положения, противные им. Математические положения мы не можем мыслить иначе, чем мы их мыслим. Напр., положение «между двумя точками нельзя провести более одной прямой» является необходимым, потому что нельзя мыслить более одной прямой между двумя точками.

Но от чего это происходит?

Это происходит от особенностей предмета математики. Науки математические имеют своим предметом пространственные отношения, числа и величины. Геометрия имеет своим предметом пространственные отношения, арифметика и алгебра определяют отношения между числами или вообще между величинами. Особенность предмета математики заключается в том, что она имеет дело не с реальными предметами, но с построениями нашего ума. Для пояснения этого возьмем в пример понятие числа. Мы приписываем числа вещам: мы говорим, что вещей большее число или что их меньшее число. Однако, как мы видели в Психологии, число не есть что-либо реальное, существующее в

157

 

 

вещах, число не находится в вещах. Поэтому оно не есть отвлечение от свойств вещей. Если бы понятие числа представляло собою такое отвлечение, какое представляют собою все другие понятия о предметах физического мира, то понятие единицы, например, не представляло бы собой такой определенности, что одна единица абсолютно равна другой. Эта определенность именно есть то, чего совершенно мы не можем утверждать относительно какого бы то ни было понятия о предметах физического мира. Отсюда следует, что понятие числа есть продукт построения нашего ума. Оттого оно обладает таким постоянством; оттого 2x2 всегда будет равняться четырем.

Точно таким же образом и пространственные элементы геометрии не суть реальные предметы, подобные тем, с которыми имеют дело науки о природе: прямая линия, точка, с которыми имеет дело геометрия, точно так же не суть отвлечения от предметов реального мира. Если бы онибыли таковыми, то они не имели бы той определенности, которой они на самом деле обладают. В природе нет абсолютно прямой линии: прямизна прямой линии, существующей в природе, может быть очень совершенна, но все же эта прямизна не будет абсолютной. В природе нет точки без протяженности. Поэтому мы можем сказать, что линии, точки и т. п., подобно числу, суть построения нашего ума: они суть продукт творчества нашего ума.

Вследствие того, что предметы математики обладают такой определенностью, проистекающей вследствие их идеального характера, т.-е. того, что они суть продукты построения нашего ума, все математические положения, касающиеся пространственных или числовых отношений, аподиктический достоверны. Таковы, например, аксиомы и определения математики.

Под аксиомами мы понимаем такие положения, которые не нуждаются в доказательстве, но которые служат для доказательства других положений. Есть аксиомы обще-математические и аксиомы чисто геометрические. К первым относятся, например, аксиомы: «две величины, порознь равные третьей, равны между собою», «часть больше целого» и т. п. К числу геометрических аксиом относятся, например, следующие: «если две величины могут быть приведены в совмещение, то они равны», «две прямые не могут замыкать пространства».

158

 

 

Аподиктическая достоверность этих положений объясняется тем, что геометрия имеет своим предметом объекты идеальные, которые вследствие этого приобретают постоянный и неизменный характер.

Что касается метода, которым пользуется математика, то он есть дедуктивный, потому что математика выводит все свои положения из нескольких основных положений, которые называются аксиомами и определениями.

Что касается математической индукции, то о ней следует заметить, что она отличается от индукции естественнонаучной тем, что выводит заключение не из множества отдельных примеров, а из одного примера или случая, чем математика также коренным образом отличается от естествознания, индукции которого в большинстве случаев являются результатом сравнения большого или меньшего ряда однородных случаев.

Естествознание. Основная задача естествознания, как мы видели, заключается в том, чтобы отыскать законы, которым подчиняются явления природы, т.-е. усмотреть правильность и закономерность в смене этих явлений. Объяснить какое-либо явление — значит показать, каким законам оно подчиняется. Метеорология, например, объясняет явления в том случае, если сводит их к каким-либо общим законам физических и химических процессов. Но так как в конце концов все химические и физические процессы могут быть сведены к каким-нибудь механическим процессам, т.-е. к процессам движения материи в том смысле, как их изучает наука механика, то мы можем сказать, что изменения неорганической материи определяются механическими законами.

Если взять какой-нибудь жизненный процесс, то он тоже, конечно, находит свое объяснение в каких либо общих законах. Эти законы можно назвать биологическими.

Между законами механическими и законами биологическими есть существенное различие в достоверности: именно, науки, которые занимаются изучением процессов неорганической материй, во-первых, с математической точностью определяют законы этих процессов, а во-вторых, их гипотезы могут быть проверяемы при помощи эксперимента. В этих науках сведение простейших явлений к общим законам

159

 

 

осуществляется с наибольшим совершенством, потому что законы физики и механики могут быть выражены при помощи числа. Так как сведение явлений к механическим процессам приводит к полной точности, то науки о неорганическом мире принято называть точными науками. Разумеется, эта точность в сравнении с точностью математики должна быть признана относительной.

Свести биологические явления к каким-нибудь более общим законам представляется чрезвычайно трудным именно потому, что они очень сложны. Идеальным, конечно, и здесь является доказательство того, что те или другие явления порождаются определенными причинами. Некоторые предполагали, что при объяснении биологических явлений необходимо пользоваться так назыв. телеологической точкой зрения, т.-е. объяснять те или другие явления из той цели, которая ими достигается, в том случае если эти явления не могут быть объяснены причинно. Напр., различные приспособления организмов не могут быть объяснены причинно, т.-е. мы не можем указать, какие причины породили их, но за то мы можем сказать, какой цели они служат. Напр., у нас в глазу есть хрусталик, благодаря изменениям которого мы можем видеть предметы отдаленные и предметы близкие. От чего это происходит, мы сказать не можем, но мы знаем, что хрусталик существует для того, чтобы у нас могло осуществляться ясное видение предметов.

Следует заметить, что эти две точки зрения совсем не исключают друг друга. При современном состоянии науки мы можем сказать, что далеко не все биологические явления получили причинное объяснение, поэтому они объясняются только телеологически; с другой стороны, если какое-нибудь явление объясняется только телеологически, то отсюда отнюдь не следует, что оно когда-нибудь впоследствии не будет объяснено причинно.

Родственной по методу с биологическими науками является психология. Она также определяет законы явлений, но ее законы не обладают тою всеобщностью, которая присуща наукам о неорганической природе. Предмет психологии и его отличие от предмета наук о природе был рассмотрен нами в Психологии.

160

 

 

История. Теперь рассмотрим особенности науки истории. По мнению некоторых, задача истории сводится к описанию последовательных моментов жизни того или другого народа или вообще народов. В этом отношении жизнь народа можно уподобить жизни отдельного индивидуума. Эту последнюю мы также можем рассматривать, как совокупность последовательных моментов, соединенных в одно целое. В этом смысле история, как и биография, имеет своим предметом нечто индивидуальное. Задача истории заключается в том, чтобы установить то, что случилось один раз, описать индивидуальное; найти же в исторических явлениях общее, закон в том смысле, в каком это понятие употребляется в естествознании, не представляется возможным.

По мнению других, в исторических явлениях могут быть открыты законы; история в этом отношения сближается с естествознанием; в социальной жизни царит такая же причинная необходимость, как и в естествознании. Подобно тому, как в физическом мире возникновение известных событий необходимо влечет за собою возникновение других событий, так и в истории те или другие явления, напр., экономические, влекут за собою необходимо те или другие моральные, интеллектуальные и т. п. явления. Напр., если у того или другого народа возникает та или другая философия, то это зависит от того, что он находится на той или иной ступени экономического развития. Его мировоззрение находится в зависимости от экономических условий, притом строго необходимо, т.-е. как только возникают те или иные экономические условия, за ними необходимо следуют те или иные философские, правовые и т. п. воззрения.

Тот взгляд, что законы социальной жизни подобны законам неорганического мира, следует считать неправильным. Между историей и естествознанием есть существенное различие.

Правда, и в общественной жизни мы усматриваем известную закономерность, известное повторение явлений; мы замечаем, что за теми или другими причинами более или менее постоянно возникают те или другие явления, напр., обеднение народа ведет к увеличению преступлений и т. п. В этом смысле можно признать существование законов

161

 

 

истории. Та наука, которая рассматривает законы социальной жизни в отличие от простого описания явлений общественной жизни, называется социологией; некоторые называют ее также философией истории. Но следует помнить, что понятие закономерности в истории не может употребляться в том строгом смысле, как в естествознании. Так наз. законы социальной жизни не имеют той точности, которая присуща законам физических наук и которая, напр. в астрономии, принимает идеальную форму. Здесь возможно предсказание явлений, притом очень точное. В науках биологических точно так же в большинстве случаев возможно предсказание, и это происходит от того, что в них возможно более или менее точное определение причинной связи явлений. В истории такое точное предсказание явлений невозможно.

В противоположность взгляду, что в истории есть законы, как мы видели, утверждалось, что предмет истории заключается в единичном, индивидуальном. Но хотя история имеет дело только с индивидуальным, из этого отнюдь не следует, что в ней не может быть применено название науки. Она есть наука в особенном смысле. Не только общее может быть предметом научного познания, но таковым может быть также и индивидуальное. Если об исторических фактах нельзя сказать, что они подчинены необходимости, т.-е. что они закономерны, то к ним можно применить понятие ценности. Не всякий индивидуальный факт является предметом истории, а только лишь тот, который имеет ценность именно для культуры, для совершенства человеческой жизни. Понятие ценности—это такое понятие, эквивалентное которому не существует в науках естественных.

Вопросы для повторения. Какое отличие математики от других наук? В чем заключается особенность предмета математики? Какое различие между науками о неорганической природе и биологическими науками? Какое значение имеет телеологическое объяснение? Какое различие между объяснением причинным и телеологическим? Какова задача истории в отличие от задачи естествознания? Каково различие между историей и социологией? Какова задача социологии?

162

 

 

ЛОГИЧЕСКИЕ УПРАЖНЕНИЯ.

(Примеры и задачи.)

К главе 3-й. О различных классах понятий.

Примеры.

Дадим логическую характеристику след. терминов: музей, должник,. невежество, добродетельный, война, граф Толстой, национальность, равный, церковь.

1) Музей. Этот термин имеет два значения:

а) Здание

b) Собрание интересных предметов.

В первом смысле это термин: общий, конкретный, положительный, абсолютный.

Во втором смысле: общий, собирательный, конкретный,. положительный, абсолютный.

2. Должник—общий, конкретный, положительный, относительный.

3. Невежество—общий, абстрактный, отрицательный, абсолютный.

4. Добродетельный—общий, положительный, абсолютный.

5. Война—общий, конкретный, положительный, абсолютный.

6. Граф Лев Толстой—единичный, положительный, конкретный, абсолютный.

7. Национальность—общий, положительный, абстрактный, абсолютный.

8. Равный—общий, положительный, конкретный, относительный.

9. Церковь. Этот термин имеет два значения:

а) Здание

b) Собрание верующих.

В первом смысле этот термин: общий, конкретный, положительный, абсолютный.

Во втором смысле: общий, коллективный, конкретный, положительный, абсолютный.

163

 

 

Задачи.

1. Найти по два примера единичных и общих терминов.

2. Найти 2 примера собирательных терминов.

3. Показать на примере употребление термина в разделительном смысле.

4. Найти по два примера отвлеченных, конкретных, отрицательных, абсолютных и относительных терминов.

5. Найти два конкретных термина и образовать из них два абстрактных.

6. Дайте логическую характеристику след. терминов: „толпа“, „цвет", „нездоровый“, „муравей“, „самый высокий человек в мире“, „нехристианин“, „организм“, „равенство“, „химик“, „черный“, „искренний“, „скука“, „хотение“.

7. Какие из следующих терминов абстрактные: неблагодарный, дом, ежечасный, грубость, индивидуальность, истина, верный, верность, желтый, желтизна, детство, книга, синий, намерение, разум, разумность.

В каком смысле употреблен термин „весь“ в след. примерах:

8. Все были оправданы.

9. Все были приведены к присяге.

10. Всех преступников переловили.

11. Весь народ восстал.

12. Весь класс был наказан.

13. Весь класс принял участие в торжестве.

 

К главе 4-й. Содержание и объем понятий.

Примеры.

1. Киты суть млекопитающие.

В этом предложении сказуемое является родом по отношению к подлежащему.

2. Некоторые люди суть поэты.

В этом предложении сказуемое есть вид подлежащего.

3. Пятиугольник есть фигура с пятью сторонами.

Здесь сказуемое есть соединение рода и видового различия.

4. Человек может изучать логику.

Здесь сказуемое есть собственный признак, так как вытекает из свойства разумности.

5. Лебеди белы.

Сказуемое есть несобственный признак, притом отделимый, потому что не принадлежит необходимо всему классу.

6. Шекспир родился в Стратфорде.

Здесь сказуемое есть неотделимый несобственный признак индивидуума Шекспир.

164

 

 

7. Умный человек строго относится к своим обязанностям.

Сказуемое—собственный признак, потому что вытекает из основных свойств умного человека.

8. Бальфур—первый министр.

Сказуемое отделимый несобственный признак.

9. Указать род, вид, видовое различие, собственный признак, несобственный признак понятий: „треугольник", „полк“, „дарвинизм".

а) Треугольник. Род: фигура

видовое различие: трехсторонняя вид: равносторонний треугольник собственный признак: углы равны 2d отделим. несобственный признак: имеющий основание в два дюйма.

b) Полк. Род: собрание солдат

видовое различие: „наиболее обширное собрание солдат“.

вид: пехота

собственный признак: управление полковым командиром

отделимый несобственный признак: носящий данную определенную форму.

с) Дарвинизм. Род: научная гипотеза

вид: нео-дарвинизм Вейсмана

видовое различие: имеющая дело с развитием организмов

собственный признак: указывает гибель некоторых организмов

отделимый несобственный признак: вызывает негодование у некоторых читателей.

 

Задачи.

1. Формулируйте закон, отношения между объемом и содержанием понятия. Покажите правильность этого закона на след. рядах понятий:

а) Железо, металл, элемент, вещество.

b) Вещество, организованная материя, животное, человек.

c) Книга, печатная книга, лексикон, латинский лексикон.

2) Расположить след. термины в ряды так, чтобы каждый термин с большим объемом стоял выше термина с меньшим объемом: Наполеон, существо, личность, католик, император, животное, правитель, неправославный.

3. Разобрать след. предложения:

а) „Правильная дробь“ — это такая дробь, в которой числитель меньше знаменателя" (показать, что в этом предложении род и что вид).

165

 

 

b) Англичане—ловкие спортсмены (к числу каких признаков относится понятие „спортсмены"?)

с) Все негры курчаво-волосые (какой признак „курчаво-волосые“?).

d) Доктор Гааз был великий филантроп.

е) Очень многие англичане храбры.

f) Тигр—хищное животное.

4. Указать род, видовое различие, собственный признак и несобственный признак следующих понятий: „золото“, дом“

 

К главе 6-й. Об определении.

Примеры:

Разобрать след. определения:

1. Свет есть отсутствие темноты.

Определение неправильное; нарушает правило 3.

2. Человек есть животное, строящие жилище.

Нарушается 1-е правило. В этом определении, кроме того, приводятся несущественные признаки. Сюда же относится определение: „человек есть животное двуногое, без перьев“.

3. Собака есть домашнее животное.

Нарушается 1-е правило. Слова: „домашнее животное“ представляют несущественный признак.

4. Существительное есть слово, обозначающее какую-либо вещь.

Определение правильное. „Слово“ есть род; „обозначающее вещь“ есть видовое различие.

5. Страдание есть дисциплина характера.

Это не есть определение.

6. Порок есть противоположность добродетели.

Определение неправильное; нарушается правило 3.

7. Тело есть эмблема или видимое украшение души.

Нарушается ииравило 4.

8. Тождество есть то, что делает вещи тождественными.

Нарушается правило 2.

9. Алкоголь есть вид лекарства.

Устанавливается несущественный признак.

10. География есть наука, которая изучает землю.

Определение правильное.

Задачи.

Разобрать след. определения:

1. Жизнь есть сумма жизненных функций.

166

 

 

2. Минеральные вещества суть те, которые не произведены силами растительной или животной жизни.

3. Квадрат есть четырехсторонняя прямолинейная фигура, все стороны которой равны.

4. Треугольник есть фигура, происходящая от рассечения конуса через его вершину плоскостью, перпендикулярной к его основанию.

5. Жидкость есть то, что может быть вылито.

6. Покой есть отсутствие беспокойства.

7. Солдат есть храбрый человек, который готов умереть за свое отечество.

8. Жираф есть животное, которое питается листвой растений, имеет длинные передние ноги и очень длинную шею.

9. Золото есть металл, атомный вес которого 196,2.

10. Цивилизация есть такое состояние общества, в котором искусства и наука более или менее развиты.

11. Невежество есть слепой руководитель.

12. Невежество есть пробел в знании.

13. Язык есть выражение мыслей при помощи слов.

14. Диалект есть форма языка, присущая какой-либо части народа.

15. Лев есть царь зверей.

16. Барометр есть инструмент, предсказывающий погоду.

17. Водород есть газ, не поддерживающий ни горения, ни дыхания.

18. Железные дороги суть средства сообщения людей между собою.

19. Гипотенуза есть сторона прямоугольного треугольника, лежащая против прямого угла.

20. Вода есть краса природы.

21. Патриций—римский гражданин, не принадлежащий к низшему сословию.

22. Мухомор есть ядовитый гриб.

23. Собака есть друг человека.

24. Ртуть-единственный жидкий при обыкновенной температуре металл.

25. Хина—жаропонижающее средство.

26. Круг есть замкнутая кривая линия.

27. Перепелка есть птица степей.

28. Ямб—двухсложная стопа с ударением на втором слоге.

29. Жизнь есть сон; смерть—пробуждение.

30. Крест есть две перекрещивающиеся перекладины.

 

К главе 7-й. О делении.

Примеры.

Разобрать след. деления:

1. Плоские фигуры делятся на криволинейные и прямолинейные.

Деление правильное; имеет одно fundamentum divisionis; имеет исчерпывающий характер, так как всякая плоская фигура должна быть или криволинейной или прямолинейной.

167

 

 

2. Перья делятся на стальные и гусиные.

Деление неполное, так как бывают перья золотые, алюминиевые и проч.

3. Животные делятся на позвоночных и беспозвоночных.

Правильное дихотомическое деление.

4. Материальные тела делятся на твердые, жидкие и газообразные.

Деление правильное.

5. Свет делится на искусственный, голубой и лунный.

Деление неправильно; различные основания.

6. Книги переплетенные и непереплетенные.

Правильное дихотомическое деление.

7. Люди делятся на цивилизованных и нецивилизованных, на духовенство и светских.

Различные основания.

8. Книги делятся на книги in-quarto, in-folio, научные и богословские.

Различные основания.

Следует отличать деление вещей от деления понятий. Если сказать: Россия делится на Европейскую и Азиатскую, то это не есть логическое деление, не есть деление понятия, а есть деление вещи. То же самое следует сказать относительно след. делении: „человек состоит из тела и души“, „вода состоит из кислорода и водорода“.

Задачи.

1. Произвести деление следующих классов: правительства, науки, логические термины.

Разобрать следующие деления:

2. Люди делятся на следующие расы: арийскую, монгольскую, африканскую и американскую.

3. Изящные искусства—на живопись, рисование, скульптуру, архитектуру, поэзию и фотографию.

4. Образы правления—на монархии, тирании, олигархические и демократические.

5. Книги—на интересные и неинтересные.

6. Люди—на дающих и берущих в займы.

7. Люди делятся на французов, азиатов, непродуктивные классы и варваров.

8. Церкви—на православные и католические, высокие и низкие.

9. Жители какого-либо города делятся на мужчин, женщин, сыновей, дочерей.

10. Люди делятся на рабочих, набожных, суеверных и безбожных.

11. Дроби бывают бóльшие единицы, меньшие единицы и равные единице.

12. Деревья бывают хвойные, низкие, строевые, плодовые.

168

 

 

13. Учебные предметы делятся на обязательные и необязательные.

14. Величины могут быть равные или неравные.

15. По силе зрения люди делятся на близоруких и дальнозорких.

16. Почва бывает плодородная и неплодородная.

17. Зубы делятся на резцы, клыки, большие и малые коренные.

18. Тела по способности распространять электрическое состояние делятся на проводников, полупроводников и непроводников.

19. Источники бывают холодные, горячие, соляные, серные.

20. Пословицы делятся на древние, новые, аллегорические, нравственные, бытовые, исторические.

21. Проволоки бывают медные, серебряные, толстые, топкие, телеграфные.

22. Греки делили всех людей на греков и варваров.

Каково это деление и правильно ли оно?

 

К главе 9-й. О суждении.

Примеры.

Придать логическую форму, т.-е. выразить при помощи суждении формы А, или Е, или J, или О следующие суждения:

1. Рыбы дышат жабрами.

= Все рыбы дышат жабрами.

2. Лень никогда не приводит к добру.

= Никакая лень не приводит к добру.

3. Прекрасное и полезное отчасти совпадают.

= Некоторые прекрасные и полезные вещи совпадают.

4. Многие из почтенных людей несчастны.

= Некоторые почтенные люди суть несчастны или = Некоторые почтенные люди не суть счастливы.

5. Только один металл жидок.

= Некоторые металлы суть жидки.

6. Не все званые избраны.

= Некоторые званые не суть избраны.

7. Только германцы суть философы.

== Ни один не-германец не есть философ или = Все философы суть Германцы.

8. Только непродолжительные войны популярны.

= Ни одна продолжительная война не была популярна или = Все популярные войны были непродолжительны.

9. Хорошая лошадь никогда не имеет дурного цвета

= Ни одна хорошая лошадь не имеет дурного цвета.

10. Хорошее начало половина дела.

= Все вещи хорошо начатые суть половина дела.

169

 

 

Задачи.

Придать логическую форму след. суждениям:

1. Не все здесь присутствующие имеют значки.

2. Только те, которые хвалят добродетель, добродетельны.

3. Никто из присутствовавших не пожелал присоединиться к этому мнению.

4. Только честные уважаемы.

5. Не все его ответы были ложны.

6. Только уроженцы Африки могут переносить климат Африки.

7. Не все то золото, что блестит.

8. Не каждый решится на подобный поступок.

9. Только заслуга достойна награды.

10. Только протестанты могут занимать английский престол.

11. Нет ничего прекрасного за исключением истины.

12. Никто, кроме мужественного, не заслуживает уважения.

13. Только дипломированные имеют право присутствовать.

14. Только немногие люди придерживаются правильного образа действий.

15. Аксиомы самоочевидны.

16. Все хорошо, что хорошо кончается.

17. Если тело нагревается, то оно расширяется.

18. Добрые люди иногда поступают дурно.

19. Немногие люди знают цену добродетели.

20. Очень многие люди действуют из эгоистических побуждений.

21. Только разумные существа ответственны.

22. Только богачи тщеславны.

23. На свете не без добрых людей.

24. Клобук не делает монаха.

25. Не всякая находка приятна.

26. Многие соли растворяются в воде.

27. Не все писатели классики.

28. Ничто не вечно под луной.

29. Жизнь прожить не поле перейти.

30. Лень мать всех пороков.

31. Ничей топор еще не коснулся этих стройных стволов молодых деревьев.

32. Не всякому слуху верь.

33. Никто не без греха.

34. От трудов праведных не наживешь палат каменных.

35. На свете не без добрых людей.

36. Часто встречаются растения, которые не имеют цветов.

37. Нет ни одного человека, который бы не признал справедливости этого положения.

38. Часть народов России принадлежит к монгольской расе.

170

 

 

К гл. 10-й. Количество подлежащего и сказуемого.

Изобразите символически при помощи кругов след. суждения:

1. Все металлы суть проводники теплоты.

2. Некоторые металлы хрупки.

3. Амальгамы суть сплавы ртути.

4. Все словари суть книги.

5. Не все книги суть словари.

6. Некоторые книги суть словари.

7. Многие растения не употребляются в пищу.

8. Некоторые христиане суть православные.

9. Некоторые животные не имеют легких.

10. Некоторые люди занимаются торговлей.

11. Только трудящиеся могут оценить отдых.

12. Ни один атом не делим.

13. Некоторые современные житейские обычаи суть древние религиозные обряды.

14. Реки суть естественные пути сообщения.

15. Все соединения металлов с кислородом суть окислы.

16. Ни одно наречие не изменяется.

17. Ни один из римских рабов не обладал гражданскими правами.

18. Все излишества губят здоровье.

19. Все хвощи суть споровые растения.

20. Все пресмыкающиеся суть позвоночные.

21. Все православные суть христиане.

22. Некоторые европейцы суть христиане.

23. Некоторые животные суть позвоночные.

24. Некоторые европейцы суть магометане.

Указать количества подлежащего и сказуемого в след. суждениях:

25. Знание есть сила.

26. Привычка притупляет чувствительность.

27. Растения лишены способности движения.

28. Все параллелограммы имеют противоположные углы равные.

29. Никоторые параллелограммы имеют равные прилежащие стороны.

30. Наука изощряет ум.

 

К гл. 11-й. О противоположении суждений.

Задачи.

Выбрать из след. суждений пары противных, противоречащих, подчиненных и подпротивных предложений.

1. Некоторые элементы известны.

2. Ни один элемент не известен.

3. Все элементы известны.

4. Некоторые элементы не известны.

171

 

 

5. Все материальные вещества обладают тяжестью,

6. Ни одно материальное вещество не обладает тяжестью.

7. Некоторые материальные вещества обладают тяжестью.

8. Некоторые материальные вещества не обладают тяжестью.

Найдите противные и противоречащие суждения для следующих суждений:

9. Все пошли за ним.

10. Все птицы пернаты.

11. Ни одно пресмыкающееся не пернато.

12. Неподвижные звезды суть самосветящиеся.

13. Немногие знают самих себя.

Сделайте все возможные противоположения след. суждений:

14. Некоторые справедливые действия выгодны.

15. Все хорошо, что кончается хорошо.

16. Честность есть лучшая политика.

17. Некоторые хорошие действия не вознаграждаются.

18. Совершенное счастье невозможно.

19. Никакое знание не бесполезно.

20. Некоторые звезды не видны.

Какие суждения могут быть выведены при признании истинности следующих суждений:

21. Все сложное разрушимо.

22. Ни один лентяй не заслуживает похвалы.

23. Некоторые растения вредны.

24. Всякий грех заслуживает порицания.

25. Числа суть величины.

26. Некоторые вещества не сложны.

Какие суждения следуют из ложности след. суждений.

27. Некоторые животные разумны.

28. Некоторые виды лжи не заслуживают порицания.

29. Все науки осуществляются благодаря опыту.

30. Ни один параллелограмм не есть равносторонний.

31. Некоторые изменения не имеют никакой причины.

32. Некоторые равноугольные треугольники суть равносторонние.

 

К гл. 13-й. О непосредственных умозаключениях.

Сделайте превращение след. суждений:

1. Все металлы полезны.

2. Все органические вещества содержат уголь.

3. Все млекопитающие суть позвоночные.

4. Все люди погрешимы.

5. Ничто великое не легко.

6. Не многие избегают несчастия.

7. Некоторые преступления вменяются.

172

 

 

8. Некоторые преступления не вменяются.

9. Ни одна планета не есть самосветящаяся.

10. Некоторые люди не суть талантливы.

Сделайте обращение след. суждений:

11. Все планеты суть небесные тела.

12. Все люди не совершенны.

13. Все планеты вращаются около своей оси.

14. Смертные не могут быть счастливыми.

15. Некоторые животные суть обезьяны.

16. Все мудрецы скромны.

17. Ни один образованный человек не суеверен.

18. Не многие люди вполне довольны.

19. Некоторые кошки не суть домашние животные.

20. Все разумные существа ответственны.

21. Ртуть есть жидкий метали.

Сделайте противопоставление след. суждений:

22. Всякая живая ткань органическая.

23. Никто не любит бесчестия.

24. Некоторые преступления не вменяются.

Произведите превращение, обращение и противопоставление след. суждений:

25. Истинный ученый скромен.

26. Мнимые величины не мыслимы.

27. Некоторые млекопитающие живут в воде.

28. Никоторые удовольствия не позволительны

29. Дуэль должна быть отвергнута с точки зрения религиозной, нравственной и правовой.

30. Некоторые знания не бесполезны.

31. Все действительно счастливые люди добродетельны.

32. Некоторые люди свободны от тщеславия.

33. Все кристаллы тверды.

34. Некоторые философы суть поэты.

 

К гл. 14-й. Правила силлогизма.

Указать в нижеследующих силлогизмах последовательно: заключение, средний, больший и меньший термины, бóльшую посылку и меньшую посылку.

1. Все люди погрешимы.

2. Все короли люди.

3. Все короли погрешимы.

4. Платина есть металл.

5. Все металлы соединяются с кислородом.

6. Платина соединяется с кислородом.

7. Готтентоты способны к воспитанию, потому что готтентоты люди, а все люди способны к воспитанию.

173

 

 

4. Ни одна рыба не кормит своих детенышей молоком.

Кит кормит детенышей молоком.

Кит не есть рыба.

Вывести заключение из следующих посылок:

5. Некоторые земноводные животные суть млекопитающие.

6. Все млекопитающие суть позвоночные.

7. Все планеты суть небесные тела.

8. Ни одна планета не есть самосветящееся тело.

Рассмотрите следующие силлогизмы; если в них нет заключения, то выведите заключение. Если силлогизм ошибочен, то покажите, в чем ошибка.

7. Ярко-красные цветы не имеют запаха.

Этот цветок не имеет запаха.

След.

8. Все люди смертны.

Ни одна собака не есть человек.

Ни одна собака не смертна.

9. Все, копирующие чужие подписи, суть злонамеренные люди.

Литографы копируют чужие подписи.

Литографы суть злонамеренные люди.

10. Все слова служат для выражения мысли.

Все жесты служат для выражения мысли.

Все жесты суть слова.

11. Некоторые человеческие действия заслуживают ненависти.

Ложь есть человеческое действие.

Ложь заслуживает ненависти.

12. Волки едят ягнят.

Это животное ест ягнят.

След.

13. Все негры имеют курчавые волосы.

Этот человек имеет курчавые волосы.

След.

14. Ни одно неорганическое тело не растет.

Кристаллы суть тела неорганические.

След.

15. Некоторые металлы жидкие.

Ртуть жидкая.

Ртуть метал.

16. Некоторые негры суть христиане.

Некоторые людоеды суть негры.

Некоторые людоеды суть христиане.

17. Некоторые негры суть христиане.

Некоторые христиане добры.

След.

18. Некоторые люди не суть белые.

Некоторые животные не суть белые.

След. 

174

 

 

К гл. 15-й. Фигуры и модусы силлогизма.

1. Какие правила силлогизмов нарушаются следующими модусами, не

обращая внимания на фигуру:

АEJ, ААЕ, JОО, JЕО, АJА, ЕЕО, AJО, ОАJ, JJJ.

2. Исследуйте правильность след. модусов:

ААА по 2-й фиг., ЕАЕ по 3-й фиг., АЕО по 4-й фиг.

Исследуйте таким же образом АJJ по 2-й и 4-й фиг., АЕО по 3-й фигуре

и JЕО, .JOO, АОЕ, ЕОО по всем фигурам.

Рассмотреть приводимые ниже силлогизмы. Если в них нет заключения, то сделать заключение. Если заключение выведено, то рассмотреть, правильно ли оно; рассмотреть также, к какой фигуре и к какому модусу относится данный силлогизм. Если в силлогизме есть ошибка, то указать, какая ошибка.

1. Все чувствующие существа одушевлены.

Все животные суть чувствующие существа.

След.

2. Ни один человек не может вполне отрешиться от вкусов своего времени.

Художники суть люди.

След.

3. Всякий справедливый человек благороден.

Некоторые ученые суть справедливы.

След.

4. Все тела, имеющие меньшую плотность, чем вода, плавают на воде.

Все тела из дерева имеют меньшую плотность, чем вода.

След.

5. Все металлы проводники электричества.

Медь есть металл.

След.

6. Ни один человек не может предсказать будущего.

Гадалки суть люди.

След.

7. Все, дающее жизненный опыт, полезно.

Некоторые ошибки дают жизненный опыт.

След.

8. Ни один взяточник не честен.

Некоторые чиновники суть взяточники.

След.

Составить силлогизмы из следующих предложений:

9. Крестовые походы не были безумием, так как они возникли из сильного религиозного воодушевления.

10. Некоторые привычки заслуживают упрека, так как они принимают страстный характер.

11. Добродетель не есть безумие, так как она облагораживает человека.

175

 

 

12. Дополнить недостающие части силлогизмов:

а) Гладиаторские игры заслуживают порицания.

b) Некоторые истины суть аксиомы.

с) Все произведения искусства несовершенны.

13. Ни одно жвачное не имеет клыков.

Все львы имеют клыки.

След.

14. Ни одно цветковое растение не размножается спорами.

Папоротник размножается спорами.

След.

15. Фосфор светится в темноте.

Данное вещество в темноте не еветится.

След.

16. Ни одно художественное произведение не должно быть лишено чувства меры.

Некот. произведения современной литературы лишены чувства меры.

След.

17. Все газы упруги.

Некоторые вещества не упруги.

След.

18. Все металлы суть проводники электричества.

Некот. тела не суть проводники электричества.

След., некоторые тела не суть металлы.

19. Ни один мужественный не боязлив.

Всякий суеверный боязлив.

След.

20. Всякий культурный народ разрабатывает науку.

Ни один пастушеский народ не разрабатывает науки.

След., ни один пастушеский народ не есть культурный народ.

21. Все правильные плоские фигуры могут быть вписаны в круг.

Некоторые параллелограммы не могут быть вписаны в круг.

След.

22. Все планеты круглы.

Колесо кругло.

Колесо есть планета.

23. Каждый честный человек прилежно занимается своим делом.

Этот человек прилежно занимается своим делом.

След., этот человек честен.

24. Составить силлогизмы по второй фигуре:

а) Человек, одержимый страстью, не обладает характером, потому что он не может владеть собою.

b) Некоторые, действующие согласно закону, не обладают нравственным характером, потому что они исполняют законное не с должным настроением.

25. Докажите следующие положения:

а) Кит не есть рыба.

b) Гунны не есть культурный народ.

176

 

 

с) Дерево не погружается в воде.

d) Некоторых книг нельзя рекомендовать.

26. Некоторые машины важны для сельского хозяйства.

Все машины суть физические приборы.

След.

27. Все параллелограммы суть четырехугольники.

Некоторые параллелограммы суть равносторонние фигуры.

След.

28. Все птицы кладут яйца.

Все птицы суть позвоночные.

Некоторые позвоночные кладут яйца.

29. Магометане не суть христиане.

Магометане суть монотеисты.

След.

30. Некоторые произведения человека некрасивы.

Все произведения человека—искусственные продукты.

След.

31. Химические элементы не разложимы.

Некоторые химические элементы суть жидкости.

След.

32. Терпентинное масло не пропускает электрического тока.

Терпентинное масло есть жидкость.

След.

33. Некоторые огорчения полезны.

Все огорчения неприятны.

След. некоторые неприятные вещи полезны.

34. Все пауки суть членистоногие.

Все пауки имеют по четыре пары ног.

След.

35. Некоторые великие дела остаются малоизвестными.

Все великие деда суть геройские подвиги.

След.

36. Все алмазы суть чистый углерод.

Некот. алмазы драгоценны.

След.

37. Страусы не могут летать.

Страусы суть птицы.

След. некоторые птицы не могут летать.

38. Некоторые религии не допускают многоженства.

Все религии освящают брак.

След.

39. Ни одно растение не может жить без влаги.

Некоторые растения живут в пустынях.

След.

40. Доказать следующие положения:

а) Некоторые птицы не летают.

b) Некоторые романы вредны.

177

 

 

с) Некоторые простые машины употребляются в домашнем обиходе.

d) Некоторые приятные общества действуют вредно на наш характер,

41. Все рыбы дышат жабрами.

Все дышащие жабрами животные живут в воде.

След. некоторые живущие в воде животные суть рыбы.

42. Все улитки суть мягкотелые.

Ни одно мягкотелое не есть млекопитающее.

След.

43. Некоторые похожие на растения существа суть кораллы.

Все кораллы суть животные.

След.

44. Ни один честный человек не прибегает ко лжи.

Прибегающие ко лжи вводят в заблуждение других.

След.

45. Ни один невежда не есть ценитель искусства.

Некот. ценители искусства суть музыканты.

След.

46. Некоторые истины, влияющие на поведение людей, суть умозрительные истины.

Все истины, влияющие на поведение людей, имеют ценность.

След.

47. Некоторые люди не глупы.

Все люди подвержены заблуждениям.

След.

48. Каждый хороший государственный деятель относится благоприятно к прогрессу.

Некоторые члены парламента не относятся благоприятно к прогрессу

След.

49. Ни один отдел науки не может быть доведен до совершенства.

Все отделы науки достойны разработки.

След.

50. Безобразие лица есть естественный недостаток.

Неграциозность не есть естественный недостаток.

Неграциозность не есть безобразие лица.

51. Некоторые минеральные соединения не разлагаются от теплоты.

Все органические вещества разлагаются от теплоты.

След.

52. Разумные существа ответственны за свои действия.

Животные не суть разумные существа.

След.

 

К главе 16-й. Сведение силлогизмов.

Следующие силлогизмы свести к первой фигуре.

1. Все германцы хорошо воспитаны.

178

 

 

Некоторые солдаты хорошо воспитаны.

2. Ни одна звезда не есть планета.

Все планеты суть круглые тела.

Некоторые круглые тела не суть звезды.

3. Некоторые судьи беспристрастны.

Все судьи независимы.

Некоторые независимые люди суть беспристрастны.

4. Нервный ток не проходит по перевязанному нерву.

Электричество проходит по перевязанному нерву.

Электричество не есть нервный ток.

5. Ни один человек не есть птица.

Все птицы суть животные.

Некоторые животные не суть люди.

6. Ни одно теплокровное не есть пресмыкающееся.

Все черепахи суть пресмыкающиеся.

След.

7. Ни один великодушный человек не мстителен.

Нек. умные люди мстительны.

След.

8. Опричники причиняли зло России.

Некот. из приближенных Иоанна Грозного не причиняли зла России

След.

9. Горение сопровождается выделением тепла.

Горение есть химический процесс.

След.

10. Некоторые лекарства суть яды.

Все лекарства суть средства исцеления.

След.

11. Ни один фанатик не отличается терпимостью.

Все фанатики слепо преданы своим идеям.

След.

12. Все проверенные гипотезы суть теории.

Некот. гипотетические положения естествознания не суть теория.

След.

13. Ни один истинный художник не считается со вкусами толпы.

Некот. истинные художники суть любимцы толпы.

След.

14. Все амебы суть корненожки.

Все корненожки суть простые животные.

След.

15. Кислород есть элемент.

Ни один элемент не разложим.

След.

16. Некоторые ученики тратят время непроизводительно.

Все тратящие время непроизводительно суть беззаботные люди.

След.

17. Ни одно беспозвоночное не есть пресмыкающееся.

179

 

 

Некот. пресмыкающиеся суть змеи.

След.

18. Все бромосеребряные соединения разлагаются от действия света,

Это соединение не разлагается от действия света.

След.

19. Все хвойные деревья сохраняют листву зимой.

Некот. хвойные деревья растут на севере.

След.

20. Все реки Кавказа питаются ледниками и снегами.

Все реки, питающиеся ледниками и снегами, суть горные реки.

След.

 

К главе 17-й. Условные, разделительные и лемматические силлогизмы.

В следующих умозаключениях показать, к какому типу они принадлежат. Где недостает заключения, следует вывести его. Если в умозаключении есть ошибка, то следует показать, какая и почему.

1. Если вода нагревается, то она испаряется.

Вода нагревается.

След.

2. Если хорошо обработать поле, то посевы не будут страдать от засухи.

Это поле хорошо обработано.

След.

3. Если земля обладает точной формой шара, то меридианные градусы в различных географических широтах должны были бы быть равны.

Но меридианные градусы в различных широтах не равны.

След.

4. Если данный стих есть гекзаметр, то он должен иметь 6 стоп.

Этот стих не есть гекзаметр, поэтому он не имеет 6 стоп.

След.

5. Если преступник не виновен, то его оправдывают.

Преступника не оправдали.

След., он виновен.

6. Если у человека отнять последнюю надежду, то он падает духом.

NN пал духом.

След.

7. Если урок труден, тоученики плохоего усваивают.

Данный урок ученики плохо усвоили.

След., данный урок труден.

8. Тиран заслуживает смерти.

Цезарь не был тираном.

Поэтому он не заслуживает смерти.

9. Если бухта замерзает, то корабли не могут входить в нее.

Корабли не могут входить в нее.

След., бухта замёрзла.

180

 

 

10. Если поезду угрожает опасность, то железнодорожный сторож выходит с красным флагом.

Железнодорожный сторож вышел не с красным флагом.

След.

11. Если бывают сильные морозы, то хлеб погибает.

Хлеб погиб.

След., были сильные морозы.

12. Если температура опустится ниже точки замерзания, то ни одно семя не прорастет.

Ни одно семя не проросло.

След.

13. Если бы Лжедимитрий 1-й был ставленником Польши и воспитанником иезуитов, то он хорошо знал бы латинский язык.

Лжедимитрий 1-й плохо знал латинский язык.

След.

14. Это лекарство или полезно, или вредно, или безразлично.

Оно полезно.

След.

15. Это действие или похвально, или постыдно, или нравственно безразлично.

Оно не похвально и не постыдно.

След.

16. Путь кометы есть или эллипс, или парабола, или гипербола.

Путь данной кометы не может быть ни параболой, ни гиперболой.

След.

17. Это действие или дозволено, или запрещено.

Оно не дозволено.

След., запрещено.

18. Всякая политическая реформа или разумна, или бесполезна.

NN реформа была бесполезна.

След., эта реформа не была противна разуму.

19. Линии бывают или прямые, или кривые, или ломаные.

Данная линия не кривая и не ломаная.

20. Позвоночные животные суть или млекопитающие, или птицы, или пресмыкающиеся, или рыбы.

Данное позвоночное животное не есть ни млекопитающее, ни птица, ни пресмыкающееся.

След.

21. Поэтические произведения бывают или эпические, или лирические, или драматические.

Сатира „Чужой толк“ Дмитриева есть произведение лирическое.

След.

22. Бактерии бывают или шарообразные, или спиральные, или палочковидные.

Бактерия возвратного тифа есть спиральная.

След.

23. Каждая область России представляет или тундру, или лес, или степь, или область вечнозеленых деревьев.

181

 

 

Эта окраина, России не представляет тундру.

След.

24. Если какая-либо наука доставляет полезные факты или изучение ее упражняет мыслительные способности, то она заслуживает изучения.

Геометрия или доставляет полезные факты или ее изучение развивает мыслительные способности.

Геометрия заслуживает изучения.

25. Если преступники суть душевно-больные, то их необходимо изолировать от общества.

Если преступники суть люди душевно-здоровые, то они должны быть наказываемы.

Но преступники суть или душевно-больные, или душевно-здоровые.

След., преступники должны быть или устранены из общества, или они должны быть наказываемы.

26. Если больной подвергнется операции, то вследствие слабости он умрет.

Если он не подвергнется операции, то умрет вследствие болезни.

Но больной или подвергнется операции, или не подвергнется ей.

След.

27. Если мы предпринимаем войну, то или должны сделать заем, или увеличить налоги, или возместить расходы на счет неприятеля.

Мы не можем сделать ни того, ни другого, ни третьего,

След., мы не можем вести войны.

28. Красивые цветы нравятся или вследствие их запаха, или вследствие их вида.

Розы нравятся вследствие их запаха.

След., розы не любимы за их внешний вид.

29. Если он отправится в город, то он должен заплатить за проезд по железной дороге и за пребывание в гостинице.

Но он не может заплатить ни за то, ни за другое.

Поэтому он не может отправиться в город.

30. Если бы он был умен, то он увидел бы свою ошибку; и если бы : он был искренен, он признался бы в ней.

Но он или не видит своей ошибки или не признается в ней.

Поэтому он или не умен, или не искренен.

31. Если бы у меня были музыкальные способности, я поступил бы в консерваторию.

Если бы у меня были коммерческие наклонности, то я начал бы торговое дело.

Но я не поступил в консерваторию и не начал торгового дела.

След.

32. Если бы у этого крестьянина была коса, то он скосил бы свою рожь.

Если бы у него был серп, то он сжал бы ее.

Но он не скосил и не сжал.

След.

33. Если расход организма превышает его приход, его организм уменьшается в весе.

182

 

 

Если приход превышает расход, то он увеличивается в весе.

Но организм не уменьшается и не увеличивается в весе.

След.

34. Если человек скуп, то он копит.

Если человек бережлив, то он тратит неумеренно.

Этот человек не копит и не тратит неумеренно.

След.

35. Если бы мы захотели помочь этому бедняку, то мы должны были бы или дать ему денег, или найти подходящее место.

Но мы не даем ему ни денег, ни подходящего места.

 След.

36. Если бы я был не злопамятен, то я забыл бы обиду.

Если бы я был кроток, то я простил бы ему.

Но я не забыл обиды и не простил ему.

След.

37. Если бы Цезарь был суеверен, то он уступил бы просьбам Кальпурнии не идти в сенат.

Если бы Цезарь был осторожен, то он удалил бы Брута.

Цезарь не уступил просьбам Кальпурнии и не удалил Брута.

След.

38. Если разнородные элементы при соединении между собою более или менее удерживают свои свойства, то они составляют механическую смесь.

Если разнородные элементы при соединении между собою превращаются в новые тела, то они образуют химическое соединение.

Разнородные элементы при соединении между собою или удерживают свои свойства или превращаются в новые тела.

След.

 

К главе 18-й. Сложные и сокращенные силлогизмы.

Дополнить недостающие части следующих силлогизмов:

1. Каждый желает добродетели, потому что каждый желает счастья.

2. Раб есть человек, а потому не следует его держать в неволе.

3. Многие оспариваемые положения заслуживают тем не менее внимания, потому что многие из таких положений могут оказаться верными.

4. Некоторые удовольствия не заслуживают одобрения. Поэтому некоторые удовольствия не суть почетны.

5. Это предположение слишком хорошо для того, чтобы его можно было осуществить.

6. У него нет вкуса к изящному, так как он не любит живопись.

Определить форму следующих сложных силлогизмов:

Все материальное находится в пространстве. Все, что находится в пространстве, протяженно. След., все материальное протяженно. Ничто протяженное не просто. След., ничто материальное не просто.

8. Кто все отрицает, тот ни во что не верит; кто ни во что не верит, находится в противоречии с самим собою (потому что он верит

183

 

 

в предложение, что все невероятно); кто находится в противоречии с самим собою, мыслит нелогично. След., кто все отрицает, мыслит нелогично.

9. Война есть орудие разрушения. Все, способствующее разрушению, враждебно культуре; все враждебное культуре вредит общему благосостоянию; но от того, что вредит общему благосостоянию, следует воздерживаться всеми возможными способами. След., от войны следует воздерживаться всеми возможными способами.

Выразить в силлогистической форме:

а) Ты царь: живи один.

b) Покойник Клит в раю не будет:

Творил он тяжкие грехи.

c) Я тебя породил, я тебя и убью.

d) Не таков Андрий, чтобы дался живым в плен.

е) Где ему, старому, идти на войну.

f) Молодость счастлива тем, что имеет будущее.

g) Хвалы приманчивы, как их не пожелать.

h) Клобук не делает монаха.

i) Ты трус, а мне не сын.

к) Не дряхлому Востоку покорить меня.

 

К главе 21-й. Об индуктивных методах исследования.

1. Когда мы ударяем звонок, находящиеся под воздушным колоколом, то звук бывает слышим в том случае, когда под колоколом есть воздух, но когда под колоколом нет воздуха, то звук не бывает слышим. (Какой отсюда можно сделать вывод и по какому методу делается этот вывод?)

2. Было найдено, что когда под колокол впускали воздух постепенно, то звук становился все громче и громче. (Какой отсюда можно сделать вывод и по какому методу делается этот вывод?)

3. Когда удаляется какая-либо часть мозга, то уничтожается какая-либо психическая функция. (Какое следует заключение и по какому методу сделано заключение?)

4. Некто начал заниматься гребным спортом, начал страдать сердцебиением; перестал заниматься этим спортом—перестал страдать сердцебиением. (Какой вывод и по какому методу?)

5. В одном обществе во время обеда все те гости, которые ели пирожное, заболели всеми признаками отравления, а те из гостей, которые не ели, остались здоровыми. (Какова причина болезни и каким методом определяется эта причина?)

6. Число преступлений и количество потребления водки возрастают и уменьшаются в одно и то же время. (Какое заключение и по какому методу?)

7. A, В, С, D, Е были членами того комитета, который отвергнул моего друга; я знаю, что A, В, С, D подавали голос за него. (Кто был причиной его неизбрания и по какому методу определяется эта причинв?)

184

 

 

8. Как можно при помощи индуктивного метода, определить причины сквозного ветра в комнате?

9. Наблюдение показало, что величина и число темных пятен, представляющий гигантские бури, происходящие на поверхности солнца, возрастают и убывают в те же периоды, в какие возникают магнитные бури на земной поверхности. (Каким методом можно определить связь между солнечными пятнами и магнитными бурями?)

10. В больнице есть две комнаты для больных детей, по обстановке совершенно тождественные, но одна из них окнами обращена к северу, а другая к югу. Здоровье детей в последней было хорошо, а в первой смертность была высока. (Какой вывод и по какому методу?)

11. Когда термометр приходит в соприкосновение с теплотой, то уровень ртути сначала несколько понижается, а затем повышается. Так как нагревание ртути производит только повышение уровня ртути, то понижение уровня ртути причиняется какой-нибудь другой причиной. (По какому методу производится заключение?)

12. Во многих случаях было найдено, что малярийная лихорадка бывает у таких больных, которые были укушены москитами. Поэтому можно было сделать заключение, что москиты причиняют лихорадку. (По какому методу сделано заключение?)

13. У меня украли в прихожей шубу. В прихожую входили лишь кухарка, дворник и какой-то незнакомый разносчик. Невиновность кухарки и дворника доказана. (Какой вывод и по какому методу?)

14. Если мы луч от раскаленного железа пропустим через какой-нибудь раскаленный газ и разложим его, то получим спектр с темными линиями. Из предыдущих опытов известно, что луч от раскаленного железа дает такой же спектр, но без темных линий. (Какой вывод и по какому методу?)

15. Наблюдения показывают, что по мере того, как увеличивается обезземеление мелких собственников, увеличивается количество пролетариата. Увеличение же количества пролетариата, создавая большие кадры свободных рабочих рук, способствует зарождению и развитию крупной промышленности. (Какой вывод и по какому методу?)

16. Замечено, что при проведении железной дороги через известную местность торговля и промышленность в этой последней развиваются. (Какой вывод и по какому методу?)

17. В стакан налили горячей воды, стакан лопнул. Стакан с холодной водой поставили в печь, стакан лопнул. У зеркала поставили лампу; на зеркале образовалась трещина. (Какой вывод и по какому методу?)

18. В низкой болотистой местности был построен каменный дом и все квартиры в нем оказались сырыми. Рядом с ним был построен деревянный дом о голландским отоплением, но и этот дом оказался сырым. Потом выстроили деревянный дом с паровым отоплением, и оказалось, что и этот дом имел тот же

185

 

 

недостаток. (Какова причина сырости этих квартир и по какому методу определяется причина?)

19. Дом обрушился. Это могло произойти или от пожара, или от землетрясения, или урагана, или наводнения, или от артиллерийского обстрела. Так как ничего подобного не было, значит дом обрушился от ветхости. (По какому методу сделано заключение?)

20. В одной из биографий Франклина рассказывается о том, как он хотел наглядно показать пользу искусственного удобрения. Для этого он засеял клевером два смежных участка земли, но предварительно один из них удобрил гипсом. На этой площадке вырос роскошный клевер, на соседней—обыкновенный. Для разъяснения этого явления перед участком с лучшим клевером Франклин поместил надпись: „здесь удобрено гипсом». (По какому методу сделан вывод?)

 

К главе 27-й. Логические ошибки.

Найти ошибки в следующих умозаключениях.

1. Все разумные существа ответственны.

Некоторые собаки разумны.

След., некоторые собаки ответственны.

2. Все углы треугольника ABC равняются двум прямым.

След., угол АВС равняется двум прямым.

3. Все, что помогает здоровью, полезно.

Мальц-экстракт помог здоровью моего друга.

Мальц-экстракт полезен.

4. Древние греки произвели величайшие образцы красноречия и философии.

Лакедемоняне были древние греки.

След., лакедемоняне произвели величайшие образцы красноречия.

5. Все сочинения Шекспира нельзя прочитать в один день.

Гамлет—сочинение Шекспира.

Гамлета нельзя прочитать в один день.

6. Невозмутимое спокойствие есть счастье.

Смерть есть невозмутимое спокойствие.

След., смерть есть счастье.

7. Все сторонники партии X защищают этот взгляд.

Вы защищаете этот взгляд.

След., вы сторонник партии X.

8. Все люди погрешимы.

Святые суть люди.

След., святые погрешимы.

9. Все классы составляют государство.

Мещане суть класс.

Мещане составляют государство.

10. Путешествие по какой-либо местности дает возможность много видеть.

Я ночью проехал по местности X.

След., я много видел.

186

 

 

11. Все англичане свободны; поэтому ни один англичанин никогда не бывает заключен в тюрьме.

12. Благосостояние Англии возросло за последние 50 лет. Мы можем это приписать влиянию свободной торговли.

13. Человек, который ничего не, делает, есть лентяй.

Этот человек ничего не делает.

След., он лентяй.

14. Какую ошибку сделал Колумб, когда он поставил яйцо, разбив конец его.

15. Если бросить зерно пшеницы на пол, то произведет ли оно звук? Нет. Тысяча зерен произведут ли звук при тех же обстоятельствах? Да. Существует ли пропорциональность между тысячью зерен и одним зерном? Да. Но если одно зерно не производит звука, то и тысяча зерен не произведут такового.

16. Вы не то, что я.

Я человек.

След., вы не человек.

17. Книги суть источник поучения и развлечения.

Таблица логарифмов есть книга.

След., таблица логарифмов есть источник поучения и развлечения.

18. Нападать на кого-либо дурно.

Солдат нападает на кого-либо.

След., солдат поступает дурно.

19. Два и три составляют пять.

След., два составляют пять и три составляют пять

20. Кто наиболее голоден, тот ест наибольше.

Кто наименьше ест, тот наиболее голоден.

След., кто ест наименьше, тот ест наибольше.

21. Все немцы педантичны.

Г. К—немец.

След., г. N педантичен.

22. Дикари украшают себя перьями.

Дамы украшают себя перьями.

След.

23. Толпа обратилась в бегство.

Этот человек был в толпе.

След., этот человек обратился в бегство.

24. В воде водятся инфузории.

В этом стакане вода.

След., в этом стакане водятся инфузории.

25. Все американцы предприимчивы.

Джонсон—американец.

След., Джонсон предприимчив.

26. Все чахоточные кашляют.

NN кашляет.

След.

27. Европейцы культурны.

187

 

 

Этот человек европеец.

След., этот человек культурен.

28. Крестьяне села N учинили самосуд над конокрадом.

Крестьянин А есть житель села N.

След., крестьянин А учинил самосуд над конокрадом.

29. Этот человек не причиняет зла людям.

След., он любит людей.

30. Лед можно принести в решете.

Лед есть замерзшая вода.

След., воду можно принести в решете.

31. Почему животные не говорят? Потому что не обладают даром речи.

32. Суд присяжных вынес оправдательный вердикт. Вы были в числе присяжных. Вы вынесли оправдательный вердикт.

33. N на наш вопрос, почему он не участвовал в выборах, отвечал: „мой голос все равно не мог иметь влияния на ход выборов“. Но также могут рассуждать и В, и С, и Д. Какова ошибка в их рассуждении?

34. Животные в ярости страшны для человека.

След., мышь в ярости страшна для человека.

35. У животных нет общих представлений. Это мы предполагаем на том основании, что у них нет способности речи. А что у них нет способности речи, предполагаем потому, что у них нет общих представлений.

36. Полумертвый то же самое, что и полуживой.

Если половины равны, то равны и целые.

След., живой равняется мертвому.

37. Все пьющие впадают в нищету и бедность.

Поэтому пьющие должны быть порицаемы.

 

Смешанные задачи.

1. Никто, кроме белых, не цивилизован.

Индейцы не белые.

След., индейцы не цивилизованы.

2. Истинный философ не зависит от прихотей судьбы, так как он находит свое главное счастье в умственном и нравственном совершенствовании.

3. Не всякая старательность добродетельна, потому что бывает старательность и неблагоразумная.   .

4. Кто не хочет учиться, тот не может сделаться образованным.

Если это так, то есть много способных людей, которые не могут сделаться образованными.

5. Только теплые страны производят вина. Испания теплая страна.

Испания производит вина.

6. Плавание возможно только в жидкостях, а поэтому невозможно в этой воде, которая замерзла.

188

 

 

7. Некоторые ученые сошли с ума.

Этот человек не ученый.

Он не сойдет с ума.

8. Милосердие только убивает, прощая убийц.

9. Подобрать посылки к след. заключениям:

а) Некоторые логики плохо рассуждают.

b) Кольца Сатурна суть материальные тела.

с) Все неподвижные звезды подчиняются закону тяготения.

10. Люди мужественные заслуживают доверия.

Люди опытные заслуживают доверия.

Поэтому люди опытные суть люди мужественные.

11. Если кто чувствует вину, тот краснеет.

Этот человек покраснел.

След., он чувствует вину.

12. Душа деятельна.

Материя не есть душа.

След., материя не есть деятельна.

13. Этот господин с широкими бровями талантлив, потому что все талантливые люди имеют широкие брови.

14. Всякий порок заслуживает порицания.

Соревнование не есть порок.

Соревнование не заслуживает порицания.

15. Некоторые позвоночные суть двуногие.

Некоторые двуногие суть птицы.

Некоторые птицы суть позвоночные.

16. Народ этой страны страдает от голода.

Вы один из народа этой страны.

Вы страдаете от голода.

17. Все, что летает по воздуху, есть птица.

Летучие мыши летают по воздуху.

След., летучие мыши суть птицы.

18. Нельзя верить истории Ливия, потому что он описывает невозможные чудеса.

19. Великобритания имела постоянные беспорядки в Египте после прорытия Суэцкого канала. Поэтому можно думать, что прорытие канала было причиной беспорядков.

20. Два и три есть четное и нечетное.

Два и три суть пять.

След., пять есть четное и нечетное.

21. Если люди хороши, то наказание излишне; если они дурны, то наказанию не придается значения. Но люди или хороши, или дурны.

След., наказанию или не придается значения, или оно бесполезно.

22. Было замечено, что экономические кризисы происходили в правильные периоды приблизительно в 10 лет. Эта десятилетняя периодичность, как кажется, соответствует подобной же периодичности плохих урожаев, а причиною этих последних является десяти-

189

 

 

летняя периодичность в возникновении солнечных пятен. (Какое заключение и по какому методу?)

23. Азот, получаемый из различных источников, имеет одну и ту же плотность. В 1894 г. лорд Релей и проф. Рамсэй, отметивши тот факт, что атмосферный азот на ½% тяжелее, пришли к открытию неизвестного до сих пор вещества, которое было названо аргоном. (По какому методу произошло это открытие?)

24. Человек, пораженный пулей в сердце, умирает. (Каким методом определяется причина смерти?)

25. Я нахожу утром ветку, отломившуюся от дерева в моем саду. Это могло произойти или от сильного ветра ночью, или это могло быть сделано вором. (Как я должен поступить, чтобы определить причину?)

26. Один критик высказал суждение о какой-то книге, прочитав всего на всего одну страницу этой книги. Когда это ему поставили в упрек, то он ответил: „Если я желаю определить вкус вина в бочке, неужели для этого я должен выпить всю бочку: одной рюмки вполне достаточно, чтобы произвести оценку". (Какая может быть ошибка в его рассуждении?)

190

 

 

Указатель литературы по логике.

Для дальнейшего изучения логики можно рекомендовать следующие сочинения на русском языке:

Джевонс. Элементарный учебник логики дедуктивной и индуктивной. Спб., 1881.

Минто. Дедуктивная и индуктивная логика. М., 1901.

Ланге. Учебник логики. Одесса, 1896.

Д. С. Милль. Система логики. 2 т. М., 1899.

Тэн и Шиль. Наведение как метод исследования природы. 1866.

Владиславлев. Логика. Обозрение индуктивных и дедуктивных приемов мышления. Спб., 1881 (с приложением истории логических учений).

Троицкий. Учебник логики. М., 1885—1888.

Гершель. Философия естествознания. Спб., 1868.

Джевонс. Основы науки. Спб., 1881.

191

 

 

Указатель терминов и имен.

(Цифры обозначают страницы.)